Системы счисления для представления информации в ЭВМ

Глава 4. Элементы теории и практики кодирования

4.1. Системы счисления для представления информации в ЭВМ

Упражнения 4.1.1.- 4.1.11.

4.2.Основные понятия вероятностной теории информации

Упражнения 4.2.1.- 4.2.3.

4.3. Обработка сообщений как кодирование

Упражнения 4.3.1.- 4.3.15

4.4. Кодирование информации как средство

обеспечения контроля работы автомата

Упражнения 4.4.1.- 4.4.17.

4.5. Основы алгебры вычетов и их приложение к простейшим криптографическим шифрам

Упражнения 4.5.1.- 4.5.3.

Системы счисления для представления информации в ЭВМ

В позиционной системе счисления (ПСС) любое действительное число А можно представить в виде суммы разложений по степеням (основания системы счисления):

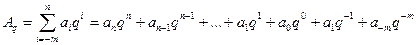(6.2.1)

с произвольным числом q>1, называемым основанием. При заданном основании число А однозначно определяется всеми коэффициентами a_i с соблюдением порядка, т.е. кортежем длины n+m+1. Общепринятым считается следующее представление:

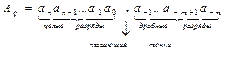
В различных позиционных системах счисления одно и то же число имеет различный вид (представление); и наоборот, одинаковой записи в разных ПСС соответствуют разные числа: например,

123321₁₀=(1·10⁵+2·10⁴+3·10³+3·10²+2·10¹+1·10⁰)₁₀=123321_абс

123321₈=(1·8⁵+2·8⁴+3·8³+3·8²+2·8¹+1·8⁰)₈=42705_абс

123321₄=(1·4⁵+2·4⁴+3·4³+3·4²+2·4¹+1·4⁰)₄=1785_абс

где под символами 1,2,3 обозначены первая, вторая и третья (после 0) цифры соответствующих ПСС:

1₈=1_абс=1₄; 2₈=2_абс=2₄; 3₈=3_абс=3₄.

Двоичная система счисления. Для представления информации в ЭВМ используется двоичная система счисления. Основание системы q=2, а алфавит состоит, соответственно, из двух чисел: 0 и 1. В двоичной системе каждый разряд имеет вес, равный 2^k , для любого kÎZ.

Вес первых 12 разрядов цифр двоичного числа представим в виде таблицы (табл.6.2):

q1=10
q2=2	211	210	29	28	27	26	25	24	23	22	21	20

Табл.6.2

Техника перевода из одной системы счисления в другую. Предлагаемые здесь действия можно проводить в любой ПСС, например в десятичной.

1) Разделить данное число на основание новой системы счисления q. Значение остатка на первом этапе деления назовем младшим значащим разрядом (МЗР).

2) Дальнейшее деление полученного частного на каждом следующем шаге дает следующие за младшим значащие разряды.

3) Процесс деления на q заканчивается, когда частное на отдельном шаге дает следующие за младшим значащие разряды.

4) Процесс деления заканчивается, когда частное на отдельном шаге окажется равным нулю. Полученный на этом этапе остаток от деления всегда меньше основания q и является старшим значащим разрядом (СЗР), расположенным крайним слева в кодовой записи числа.

5) Полученная запись всех остатков от деления слева направо (от СЗР к МЗР) и есть запись числа в новой системе счисления.

Шестнадцатиричная система счисления.Система счисления с основанием q=16 (16=2²) дает самую компактную запись числа в ЭВМ. Для перевода двоичного числа в эту систему разобъем двоичную запись на четверки – тетры, заменим их соответствующим эквивалентом в шестнадцатеричной системе, пользуясь таблицей перевода (табл.6.3).

Десятичное число	Двоичное число	Восьмиричное число	Шестнадцати-ричное число
			A B C D E F

Табл.6.3

Задано слово над множествомM, если слово составлено из элементов множества M. Для множества двоичных символов Е₂={0;1} двоичным словом длины n будет последовательность знаков, содержащая k нулей и l единиц, причем k+l=n. Так, кортеж 010111 есть слово над Е₂, двоичный код некоторого числа, содержащий k=2 нулей и l=4 единиц (т.е. слово длины 6 над множеством двоичных символов {0;1}).