Отношения между суждениями. 1. Суждение как форма мышления
План лекции
1. Суждение как форма мышления. Суждение и предложение.
2. Простые суждения.
3. Отношения между суждениями.
4. Сложные суждения.
5. Модальность суждения.
Литература
1. Гетманова, А. Д. Логика: учебник / А. Д. Гетманова. – 15-е изд., стер. – М.: Омега-Л, 2010. – 415 с.
2. Гусев, Д. А. Логика: учеб. пособие для вузов / Д. А. Гусев. – М.: МПСИ, 2010. – 376 с.
3. Ивин, А. А. Логика: учеб. пособие для студентов вузов / А. А. Ивин. – М.: Оникс: Мир и Образование, 2008. – 336 с.
4. Купарашвили, М. Д. Логика: учебное пособие для студентов / М. Д. Купарашвили, А. В. Нехаев и др. – Омск: Изд-во ОмГУ, 2005. – 124 с.
5. Никифоров, А. Л. Логика и теория аргументации / А. Л. Никифоров. – М.: Современный гуманитарный институт, 2005. – 272 с.
6. Черняк, Н. А. Логика: учебное пособие / Н. А. Черняк. – Омск: Изд-во ОмГУ, 2004. – 84 с.
Суждение как форма мышления. Суждение и предложение
Более сложной по сравнению с понятием формой мышления выступает суждение – форма мышления, в которой что-либо утверждается или отрицается о предметах, их свойствах или отношениях.
Структура простого суждения всегда трехчленна: субъект – связка – предикат.
Субъект – то, о чем говорится в данном высказывании. Предикат – то, что говорится о субъекте.
Связка устанавливает или отрицает наличие связи между предикатом и субъектом. Она бывает в двух формах – утвердительной («есть») и отрицательной («не есть»).
Пример.
Человек не есть животное.
Субъект (S) – «человек».
Предикат (P) – «животное».
Связка в отрицательной форме – «не есть».
Структуру простого суждения можно выразить в следующем виде:
S есть (не есть) Р.
Субъект и предикат называется терминами суждения. Каждый из них играет особую познавательную роль. Субъект суждения отражает то, о чем мы судим, т. е. предмет суждения. Он содержит исходное знание. В предикате отражается признак предмета, то, что говорится о предмете суждения; он содержит новое знание о нем.
В суждениях «Некоторые электростанции являются атомными электростанциями» и «Все студенты сдали зачет» субъектами являются соответственно понятия «электростанция» и «студент», предикатами – «атомная электростанция» и «сдали зачет», кванторами – «некоторые» и «все».
Суждение составляет идеальную, смысловую сторону предложения. При изучении вопроса о соотношении суждения и предложения особое внимание необходимо обратить на их сходство и различие.
Обычно суждения выражаются повествовательными предложениями, которые содержат какое-то сообщение, информацию. По цели высказывания предложения делятся на повествовательные, побудительные и вопросительные.
Вопросительные предложения не содержат в своем составе суждения, так как в них ничего не утверждается и не отрицается и они нс истинны и не ложны. Например: «Когда начнется лекция?» или «Чем будешь заниматься в свободное время?». Если в предложении выражен риторический вопрос, например: «Какой русский не любит быстрой езды?» или «Есть ли что-нибудь чудовищнее неблагодарного человека?», в таком предложении содержится суждение.
Побудительные предложения выражают побуждение собеседника к совершению действия (предложение может выражать совет, просьбу, обычное побуждение, приказ и т. д.). Все побудительные предложения не выражают суждений. Например, следующие команды: «Встать!», «Смирно!», «Правое плечо вперед!» и т. п.
Простые суждения
К простым суждениям относятся такие, которые выражают связь двух понятий и имеют структуру:
S есть (не есть) Р.
В зависимости от того, что утверждается или отрицается в простых суждениях: принадлежность признака предмету, отношение между предметами или факт существования предмета, – они делятся на атрибутивные, суждения с отношениями, экзистенциальные.
1. Суждения, в которых признак предмета приписывается (или отрицается) предмету, называются атрибутивными суждениями (суждения свойства). Например: «Никто из судей не вправе воздерживаться от голосования».
2. Суждениями с отношениями. В этих суждениях говорится об отношениях между предметами. Например: «Саратов расположен севернее Волгограда».
3. Суждения, выражающие факт существования (или не существования) предмета, называются экзистенциальными. Например: «Не существует беспричинных явлений».
В рассуждениях могут использоваться суждения, предикат которых относится не к одному, а к двум или более субъектам, например: «Студенты и школьники являются учащимися». Это суждение является сложным, состоящим из двух простых: «Студенты являются учащимися» и «Школьники являются учащимися». Но так как все два суждения имеют один и тот же предикат, оно может рассматриваться как простое, имеющее сложный субъект. Иногда суждения отражают принадлежность предмету нескольких признаков. Например: «На перемене студенты пили кофе и ели пирожное». Это суждение является сложным, состоящим из двух простых, но его можно рассматривать как простое с одним сложным предикатом.
Атрибутивные суждения называются в традиционной логике категорическими суждениями, так как они выражаются в безусловной, не допускающей иных толкований, форме. С точки зрения качества связки категорические суждения делятся на утвердительные и отрицательные. В утвердительных суждениях логическая связка («есть») приписывает предикат субъекту, например: «Человек есть животное». В отрицательных суждениях логическая связка отделяет предикат от субъекта.
С точки зрения объема субъекта категорические суждения делятся на единичные, частные и общие. В единичных суждениях объем субъекта состоит из одного элемента, например: «Иванов сдал экзамен».
В частных суждениях содержание предиката относится только к части элементов объема субъекта. Например, «Некоторые российские граждане являются студентами».
В общих суждениях предикат относится ко всем элементам объема субъекта. Например: «Все студенты нашей группы пришли на лекцию».
Объединенная классификация по качеству и количеству совмещает в себе деление суждений по качеству и количеству. В ней высказывания делятся на четыре группы:
1) общеутвердительные суждения (утвердительные по качеству связки и общие по объему субъекта).
Формула: Все S есть Р;
2) общеотрицательные суждения (отрицательные по качеству связки и общие по объему субъекта).
Формула: Ни одно S не есть Р;
3) частноутвердительные (утвердительные по качеству связки и частные по объему субъекта).
Формула: Некоторые S есть Р;
4) частноотрицательные (отрицательные по связке и частные по объему субъекта).
Формула: Некоторые S не есть Р.
Выделяющим называется суждение, отражающее факт принадлежности (непринадлежности) признака только данному предмету.Например: «Только Иванов не сдал экзамен».
Исключающими называются суждения, в которых говорится о принадлежности данного свойства всем предметам данного класса, кроме некоторой их части.Например: «Все студенты данной группы, за исключением Иванова, сдали экзамены». Исключающие суждения выражаются предложениями со словами «за исключением», «кроме», «не считая» и т. д.
Термин называется распределенным в том случае, если он в суждении берется в полном объеме.
Если термин в суждении берется не в полном объеме, то он является нераспределенным.
Правило распределенности терминов: Субъект распределен в общих суждениях и нераспределен в частных, предикат распределен в отрицательных и, как правило, нераспределен в утвердительных суждениях.
Рассмотрим общеутвердительные, общеотрицательные, частноутвердительные и частноотрицательные суждения с точки зрения распределенности в них терминов.
1) Суждение «Все металлы электропроводны». S – «металлы», Р – «электропроводны». Субъект взят в полном объеме («Все металлы»). Он распределен. Признак «электропроводность» абстрагирован не только из металлов, но и из жидкостей газов и пр. т. е. объем понятия «электропроводность» значительно шире объема понятия «металлы». В данном суждении все элементы объема субъекта совпадают только с частью элементов объема предиката, т. е. в данном суждении предикат нераспределен.
2) Суждение «Ни один кит не является рыбой». S – «кит», Р – «рыба». Субъект взят в полном объеме («Ни один», т. е. все без исключения). Он распределен. В общеотрицательных суждениях все элементы объема предиката полностью исключаются из объема субъекта, т. е. предикат в таких суждениях берется в полном объеме. Он распределен.
3) Суждение «Некоторые студенты являются спортсменами». S – «студенты», Р – «спортсмены». В частноутвердительных суждениях субъект всегда не распределен, так как понятие, стоящее на месте субъекта, берется не в полном объеме («некоторые», т.е. часть), а предикат, как правило, распределен.
4) Суждение «Некоторые студенты не являются спортсменами». S – «студенты», Р – «спортсмены». В частноотрицательных суждениях термин на месте субъекта всегда не распределен, а термин на месте предиката всегда распределен. Объясняется это тем, что все элементы объема предиката полностью исключаются из части объема субъекта. В приведенном выше примере все виды спортсменов полностью исключаются из части студентов, т. е. субъект берется не в полном объеме, а предикат – в полном объеме.
Отношения между суждениями
Суждения, как и понятия, бывают сравнимыми и несравнимыми. Сравнимыесуждения имеют одинаковые субъекты и предикаты, но могут отличаться кванторами и связками, а несравнимыесуждения имеют различные субъекты и предикаты. Например, суждения: «Все школьники изучают математику» и «Некоторые школьники не изучают математику»являются сравнимыми: у них совпадают субъекты и предикаты, а кванторы и связки различаются. Суждения: «Все школьники изучают математику» и «Некоторые спортсмены – это олимпийские чемпионы»являются несравнимыми: субъекты и предикаты у них не совпадают. Сравнимые суждения также называются идентичными по материалу.Они бывают, как и понятия, совместимыми и несовместимыми и могут находиться в различных отношениях между собой. Совместимыминазываются суждения, которые могут быть одновременно истинными. Например, суждения: «Некоторые люди – это спортсмены» и «Некоторые люди – это не спортсмены» являются одновременно истинными и представляют собой совместимые суждения. Несовместимыминазываются суждения, которые не могут быть одновременно истинными: истинность одного из них обязательно означает ложность другого. Например, суждения: «Все школьники изучают математику» и «Некоторые школьники не изучают математику»не могут быть одновременно истинными и являются несовместимыми (истинность первого суждения с неизбежностью приводит к ложности второго).
Совместимые суждения могут находиться в следующих отношениях.
1. Равнозначность – это отношение между двумя суждениями, у которых и субъекты, и предикаты, и связки, и кванторы совпадают. Например, суждения: «Москва является древним городом» и «Столица России является древним городом»находятся в отношении равнозначности.
2. Подчинение – это отношение между двумя суждениями, у которых предикаты и связки совпадают, а субъекты находятся в отношении вида и рода. Например, суждения: «Все растения являются живыми организмами» и «Все цветы (некоторые растения) являются живыми организмами» находятся в отношении подчинения.
3. Частичное совпадение(или субконтрарность) – это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения: «Некоторые грибы являются съедобными» и «Некоторые грибы не являются съедобными»находятся в отношении частичного совпадения. Необходимо отметить, что в этом отношении находятся только частные суждения – частноутвердительные I и частноотрицательные О.
Несовместимые суждения могут находиться в следующих отношениях.
1. Противоположность(или контрарность) – это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения: «Все люди являются правдивыми» и «Все люди не являются правдивыми»находятся в отношении противоположности. В этом отношении могут быть только общие суждения – общеутвердительные А и общеотрицательные Е. Важным признаком противоположных суждений является то, что они не могут быть одновременно истинными, но могут быть одновременно ложными. Так, два приведенных выше в качестве примера противоположных суждения не могут быть одновременно истинными, но могут быть одновременно ложными: неправда, что все люди являются правдивыми, но также неправда, что все люди не являются правдивыми. Противоположные суждения могут быть одновременно ложными, потому что между ними, обозначающими какие-то крайние варианты, всегда есть третий, средний, промежуточный вариант. Если этот средний вариант будет истинным, то два крайних окажутся ложными. Между противоположными (крайними) суждениями: «Все люди являются правдивыми» и «Все люди не являются правдивыми» есть третий, средний вариант: «Некоторые люди являются правдивыми, а некоторые не являются таковыми»,который, будучи истинным суждением, обусловливает одновременную ложность двух вышеуказанных крайних, противоположных суждений.
2. Противоречие(или контрадикторность) – это отношение между двумя суждениями, у которых предикаты совпадают, связки являются различными, а субъекты отличаются своими объемами, то есть находятся в отношении подчинения (вида и рода). Например, суждения: «Все люди являются правдивыми» и «Некоторые люди не являются правдивыми» находятся в отношении противоречия. Важным признаком противоречащих суждений, в отличие от противоположных, является то, что между ними не может быть третьего, среднего, промежуточного варианта. В силу этого два противоречащих суждения не могут быть одновременно истинными и не могут быть одновременно ложными: истинность одного из них обязательно означает ложность другого, и наоборот – ложность одного обусловливает истинность другого.
Рассмотренные отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата, который был разработан еще средневековыми логиками.
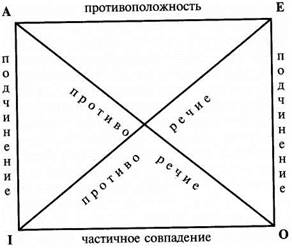
Как видим, вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Так, суждения вида А и вида I, а также суждения вида Е и вида О находятся в отношении подчинения. Суждения вида А и вида Е находятся в отношении противоположности, а суждения вида I и вида О – частичного совпадения. Суждения вида А и вида О, а также суждения вида Е и вида I находятся в отношении противоречия. Неудивительно, что логический квадрат не изображает отношение равнозначности, потому что в этом отношении находятся одинаковые по виду суждения, то есть равнозначность – это отношение между суждениями А и А, I и I, E и Е, О и О. Чтобы установить отношение между двумя суждениями, достаточно определить, к какому виду относится каждое из них. Например, надо выяснить, в каком отношении находятся суждения: «Все люди изучали логику» и «Некоторые люди не изучали логику».Видя, что первое суждение является общеутвердительным А, а второе частноотрицательным О, мы без труда устанавливаем отношение между ними с помощью логического квадрата – противоречие. Также суждения: «Все люди изучали логику» (А) и «Некоторые люди изучали логику» (I) находятся в отношении подчинения, а суждения: «Все люди изучали логику» (А) и «Все люди не изучали логику»(Е) находятся в отношении противоположности.
Как уже говорилось, важным свойством суждений, в отличие от понятий, является то, что они могут быть истинными или ложными. Что касается сравнимых суждений, о которых идет речь в данном параграфе, то истинностные значения каждого из них определенным образом связаны с истинностными значениями остальных. Так, если суждение вида А является истинным или ложным, то три других (I, E, О) сравнимых с ним суждения (то есть имеющих сходные с ним субъекты и предикаты) в зависимости от этого (то есть от истинности или ложности суждения вида А) тоже являются истинными или ложными. Например, если суждение вида А: «Все тигры – это хищники» является истинным, то суждение вида I: «Некоторые тигры – это хищники» также является истинным (если все тигры – хищники, то и часть из них, то есть некоторые тигры – это тоже хищники), суждение вида Е: «Все тигры – это не хищники» является ложным, и суждение вида О: «Некоторые тигры – это не хищникитакже является ложным». Таким образом, в данном случае из истинности суждения вида А вытекает истинность суждения вида I и ложность суждений вида Е и вида О (разумеется, речь идет о сравнимых суждениях, то есть имеющих одинаковые субъекты и предикаты).
Далее представлены все случаи отношений между истинностными значениями простых сравнимых суждений.
1. Если суждение вида А является истинным, то суждение вида Iтакже является истинным, а суждения вида Е и О являются ложными.
2. Если суждение вида А является ложным, то суждение вида I является неопределенным по истинности (то есть может быть как истинным, так и ложным, в зависимости от того, о чем будет идти в нем речь), суждение вида Е является также неопределенным по истинности, а суждение вида О является истинным. (Далее будем применять сокращения, например, вместо выражения «суждение вида А» будем говорить «А», а вместо «является истинным» – просто «истинно»).
3. Если Е истинно, то А ложно, Iложно, О истинно.
4. Если Е ложно, то А неопределенно по истинности, I истинно, О неопределенно по истинности.
5. Если I истинно, то А неопределенно по истинности, Е ложно, О неопределенно по истинности.
6. Если I ложно, то А ложно, Еистинно, О истинно.
7. Если О истинно, то А ложно, Е неопределенно по истинности, I неопределенно по истинности.
8. Если О ложно, то А истинно, Е ложно, I истинно.
Используя рассмотренные правила, можно делать выводы об истинности простых сравнимых суждений с помощью логического квадрата (или, как часто говорят в логике, по логическому квадрату). Выше был приведен пример таких выводов на основе суждения вида А: «Все тигры являются хищниками», где из его истинности вытекали определенные истинностные значения других суждений – I, Е, О. Рассмотрим еще один пример. Возьмем суждение вида Е: «Все планеты не являются звездами» и сделаем из его истинности выводы об истинностных значениях суждений А, I, О. Когда данное суждение вида Е истинно (см. правила выше), то суждение вида А: «Все планеты являются звездами» ложно, суждение вида I: «Некоторые планеты являются звездами» также ложно, а суждение вида О: «Некоторые планеты не являются звездами»истинно (если все планеты не являются звездами, то и часть планет, то есть некоторые планеты, – это тоже не звезды).
Сложные суждения
Сложным называется суждение, которое состоит из простых суждений, соединенных каким-либо союзом. В зависимости от этого союза выделяется, как правило, шесть видов сложных суждений.
Конъюнктивное суждение, или конъюнкция,– это сложное суждение с соединительным союзом «и», который обозначается в логике условным знаком Ù. С помощью этого знака конъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы аÙb (читается «а и b»), где а и b – это два каких-либо простых суждения. Например, сложное суждение: «Сверкнула молния, и загремел гром» является конъюнктивным, или конъюнкцией, (соединением) двух простых суждений: 1. «Сверкнула молния». 2. «Загремел гром». Конъюнкция может состоять не только из двух, но и из большего количества простых суждений. Например: «Сверкнула молния, и загремел гром, и пошел дождь» (аÙbÙс).
Дизъюнктивное суждение, или дизъюнкция,– это сложное суждение с разделительным союзом «или».Дизъюнктивные суждения делятся на два вида.
Нестрогая дизъюнкция– это сложное суждение с разделительным союзом «или» в его неисключающем (нестрогом) значении, который обозначается условным знаком Ú. С помощью этого знака нестрогое дизъюнктивное суждение, состоящее из двух простых суждений можно представить в виде формулы aÚb (читается «а или b»), где а и b – это два каких-либо простых суждения. Например, сложное суждение: «Он изучает английский или он изучает немецкий» является нестрогим дизъюнктивным, или нестрогой дизъюнкцией, (разделением) двух простых суждений: 1. «Он изучает английский». 2. «Он изучает немецкий». Как видим, эти суждения друг друга не исключают, ведь возможно изучать и английский, и немецкий одновременно, в силу чего данная дизъюнкция является нестрогой.
Строгая дизъюнкция– это сложное суждение с разделительным союзом «или» в его исключающем (строгом) значении, который обозначается условным знаком Ú. С помощью этого знака строгое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы aÚb (читается «или а, или b»), где а и b – это два каких-либо простых суждения. Например, сложное суждение: «Он учится в 9 классе или он учится в 11 классе» является строгим дизъюнктивным, или строгой дизъюнкцией, (разделением) двух простых суждений: 1. «Он учится в 9 классе». 2. «Он учится в 11 классе». Обратим внимание на то, что эти суждения друг друга исключают, ведь невозможно одновременно учиться и в 9, и в 11 классе (если он учится в 9 классе, то обязательно не учится в 11 классе, и наоборот), в силу чего данная дизъюнкция является строгой. Как нестрогая, так и строгая дизъюнкция могут состоять не только из двух, но и из большего числа простых суждений. Например: «Он изучает английский или он изучает немецкий, или он изучает французский» (aÚbÚc) или «Он учится в 9 классе или он учится в 10 классе, или он учится в 11 классе» (aÚbÚc).
Импликативное суждение, или импликация,– это сложное суждение с условным союзом «если... то», который обозначается условным знаком ®. С помощью этого знака импликативное суждение, состоящее из двух простых суждений, можно представить в виде формулы а®b (читается «если а, то b»), где а и b – это два каких-либо простых суждения. Например, сложное суждение: «Если вещество является металлом, то оно электропроводно» представляет собой импликативное суждение, или импликацию, (причинно-следственную связь) двух простых суждений: 1. «Вещество является металлом». 2. «Вещество электропроводно». Как видим, в данном случае эти два суждения связаны таким образом, что из первого вытекает второе (если вещество – металл, то оно обязательно электропроводно), однако из второго не вытекает первое (если вещество электропроводно, то это вовсе не означает, что оно является металлом). Первая часть импликации называется основанием, а вторая – следствием: из основания вытекает следствие, но из следствия не вытекает основание. Формулу импликации «а®b» можно прочитать так: «если а, то обязательно b, но если b, то не обязательно а».
Эквивалентное суждение, или эквиваленция, – это сложное суждение с союзом «если... то» не в его условном значении (как в случае с импликацией), а в тождественном (эквивалентном). В данном случае этот союз обозначается условным знаком ↔, с помощью которого эквивалентное суждение, состоящее из двух простых суждений, можно представить в виде формулы а↔b (читается «если а, то b, и если b, то а»), где а и b – это два каких-либо простых суждения. Например, сложное суждение: «Если число является четным, то оно делится без остатка на 2» представляет собой эквивалентное суждение, или эквиваленцию, (равенство, тождество) двух простых суждений: 1. «Число является четным». 2. «Число делится без остатка на 2». Нетрудно заметить, что в данном случае два суждения связаны так, что из первого вытекает второе, а из второго – первое: если число четное, то оно обязательно делится без остатка на 2, а если число делится без остатка на 2, то оно обязательно четное. Понятно, что в эквиваленции, в отличие от импликации, не может быть ни основания, ни следствия, так как две ее части являются равнозначными суждениями.
Отрицательное суждение или отрицание – это сложное суждение с союзом «неверно, что...», который обозначается условным знаком Ø. С помощью этого знака отрицательное суждение можно представить в виде формулы Øа (читается «неверно, что а»), где а – это какое-либо простое суждение. Здесь может возникнуть вопрос – где же вторая часть сложного суждения, которую мы обычно обозначали символом b? В записи Øа уже присутствуют два простых суждения: а – это какое-то утверждение, а знак Ø – это его отрицание, то есть перед нами как бы два простых суждения – одно утвердительное, другое отрицательное. Пример отрицательного суждения: «Неверно, что все мухи являются птицами».
Итак, мы рассмотрели шесть видов сложных суждений: конъюнкцию, дизъюнкцию нестрогую и дизъюнкцию строгую, импликацию, эквиваленцию и отрицание.
Союзов в естественном языке много, но все они по смыслу сводятся к рассмотренным шести видам, и любое сложное суждение относится к одному из них. Например, сложное суждение: «Уж полночь близится, а Германа все нет» является конъюнкцией, потому что в нем союз «а» употребляется в роли соединительного союза «и». Сложное суждение, в котором вообще нет союза: «Посеешь ветер, пожнешь бурю» является импликацией, так как два простых суждения в нем связаны по смыслу условным союзом «если... то».
Любое сложное суждение является истинным или ложным в зависимости от истинности или ложности входящих в него простых суждений. Ниже приведена таблица истинности всех видов сложных суждений в зависимости от всех возможных наборов истинностных значений двух входящих в них простых суждений (таких наборов всего четыре: 1) оба простых суждения истинные; 2) первое суждение истинное, а второе ложное; 3) первое суждение ложное, а второе истинное; 4) оба суждения ложные).
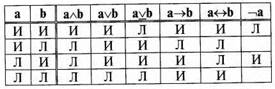
Как видим, конъюнкция (аÙb) истинна только тогда, когда истинны оба простых суждения, входящих в нее. Надо отметить, что конъюнкция, состоящая не из двух, а из большего количества простых суждений, также истинна только в том случае, когда истинны все входящие в нее суждения. Во всех остальных случаях она является ложной. Нестрогая дизъюнкция (aÚb), наоборот, истинна во всех случаях за исключением того, когда оба входящих в нее простых суждения ложны. Нестрогая дизъюнкция, состоящая не из двух, а из большего количества простых суждений, также ложна только тогда, когда ложны все входящие в нее простые суждения. Строгая дизъюнкция (aÚb) истинна только тогда, когда одно входящее в нее простое суждение истинно, а другое ложно. Строгая дизъюнкция, состоящая не из двух, а из большего количества простых суждений, истинна только в том случае, если истинно только одно из входящих в нее простых суждений, а все остальные ложны. Импликация (а®b) ложна только в одном случае – когда ее основание является истинным, а следствие ложным. Во всех остальных случаях она истинна. Эквиваленция (а↔b) истинна тогда, когда два составляющих ее простых суждения истинны или же когда они оба являются ложными. Если одна часть эквиваленции истинна, а другая ложна, то эквиваленция ложна. Проще всего определяется истинность отрицания: когда утверждение (а) истинно, его отрицание (Øа) ложно; когда утверждение (а) ложно, его отрицание (Øа) истинно.
Модальность суждения
Под модальностью в формальной логике понимают выраженную в суждении дополнительную оценочную информацию о связях между явлениями, о логическом статусе суждения, о регулятивных, временных и других его характеристиках.
В модальном суждении явно иди неявно используется модальный оператор: «возможно», «необходимо», «доказано», «плохо», «запрещено» и т. д. Например: «Плохо, когда студент пропускает занятия но неуважительной причине». Структура этого суждения такая: M (S есть Р). В широком смысле слова любая дополнительная информация в суждении называется модальностью данного суждения.
Существует большое разнообразие модальностей, которые разделены па классы. Но мы рассмотрим только вида модальностей, которые считаются наиболее часто употребляемыми в познавательном процессе: алетическую, эпистемическую и деонтическую.
1. Алетическая модальность («алетический» – слово греческого происхождения, означает «истинный») – это выражаемая с помощью операторов «необходимо», «случайно», «возможно», «невозможно» информация о логической либо фактической обоснованности суждения.
Суждения бывают ложными или истинными в силу некоторых факторов, которые можно разделить на две части: фактические и логические. Это определяет соответствующие типы модальностей: фактическую модальность и логическую модальность.
Фактическая модальность связана с объективной обусловленностью суждений, когда их истинность и ложность определяются реальным положением дел в окружающей действительности.
К фактически истинным относятся суждения, в которых связь между терминами суждения соответствует действительным отношениям между явлениями.Пример такого суждения: «СибГУФК находится в Омске».
К фактически ложным относятся суждения, в которых связь между субъектом и предикатом не соответствует реальности:«СибГУФК находится в Берлине». Поэтому здесь следует использовать модальный оператор: «Неверно, что СибГУФК находится в Берлине».
Использование модальных понятий необходимости и случайности, возможности и невозможности происходит при выражении действительных связей между явлениями. Фактическую модальность, в свою очередь, можно разделить на фактически необходимую, фактически случайную, фактически возможную и фактически невозможную виды.
Фактически необходимые – это суждения, в которых говорится о связи явлений, определяемой их устойчивой внутренней основой и совокупностью условий их развития.Таковыми являются научные законы. Например: «Во всех инерциальных системах все механические процессы происходят одинаковым образом». В естественном языке фактически необходимые суждения часто выражают с помощью слов «обязательно», «непременно», «необходимо» и т. н. Например: «Вода непременно закипит при 100 градусах Цельсия при нормальных условиях». Все остальные фактические суждения относятся к случайным.
Фактически случайные – это суждения, в которых говорится о связи, определяемой внешними, побочными для данного явления причинами. К случайным относятся суждения, которые не являются необходимыми. Их истинность и ложность определяются конкретными условиями, имеющими единичный характер. Например, суждение «Великая Отечественная война началась 22 июня 1941 года» является фактически случайным, ибо война могла начаться как до, так и после этой даты. Как известно, Гитлер неоднократно откладывал начало военных действий.
Фактически возможные – это суждения, содержащие информацию о единой основе развития явлений.Например: «В Омске сегодня, может быть, пойдет дождь». В естественном языке показателями суждений возможности являются следующие слова: «возможно», «может быть», «допускается». Они употребляются в качестве вводных слов, сказуемых.
Фактически невозможные – это суждения, содержащие информацию об отсутствии единой основы развития явлений.Например: «Обучение в вузе невозможно для человека, не имеющего среднего образования».
Логическая модальность – это информация об обусловленности суждения, которая основывается на законах и правилах логики. В нем истинность или ложность определяется структурой суждения. К ним, например, относятся суждения, выражающие законы логики (закон тождества: Всякая мысль в процессе рассуждения должна быть тождественна самой себе). К логически ложным относят внутренне противоречивые суждения. Например: «Я так тебя люблю, что ненавижу».
2. Эпистемическая модальность – это выраженная в суждении информация об основании и степени его достоверности («эпистема» означена в античной философии высший тип несомненного, достоверного знания).
Общение между людьми предполагает использование различных оценок и фактических данных, имеющих разную степень достоверности, которая зависит от многих условий. Важнейшими среди них являются логические и нелогические условия, предопределяющие два эпистемических типа суждений: рационально обоснованные суждения, выражающие знание,и основанные на вере суждения, имеющие иррациональный характер.
Ориентированное на логику познание предполагает принятие в качестве истинных лишь таких суждений, которые опираются на достоверно установленные эмпирическим или теоретическим путем данные.
В логике по степени обоснованности различают два класса суждений: достоверные (например, таковым можно считать суждение «Правильно, что живые организмы являются огромной геологической силой, как аргументировано доказал В. И. Вернадский») и проблематичные (например, «По-видимому, жизнь существует не только на Земле»).
Достоверное суждение – это такое высказывание, в котором содержится твердо установленная информация. Суждения, истинность которых обоснована, служат в познании в качестве исходного пункта новых логических выводов, приводящих к дальнейшему расширению достоверного знания. Достоверные суждения следует отличать от проблематичных.
Проблематичные суждения – это такие высказывания, которые нельзя считать достоверными в силу того, что истинность или ложность таких суждений точно не установлена.Они лишь претендуют быть истинными. Поэтому необходимо разрешить проблему: является ли содержащаяся в суждении информация достоверной? Поэтому их назвали проблематичными. В естественном языке в таких высказываниях обычно используют такие вводные слова, как «вероятно», «по-видимому», «возможно» и др.
К нелогическим факторам, которые воздействуют на человека, «заставляя» его признавать те или иные суждения в качестве истинных или ложных, можно отнести следующие: прагматический интерес, традиции, мнение авторитетов, внушение и т. н. По эпистемическому положению любые суждения, обоснованные верованием, отличаются иррациональным и эмоциональным, без критического анализа их принятием субъектом. Несмотря на их иррациональность, они могут быть с социальной точки зрения прогрессивными, но чаще они носят реакционный характер.
3. Деонтическая модальность (слово «деонтический» означает в греческом языке «обязанность») – это выраженная в суждении информация, побуждающая людей к определенным поступкам.В естественном языке высказывание строится в форме совета, пожелания, команды, правила поведения или приказа. Например: «Лекции по логике желательно слушать с большим вниманием» или «Не рекомендуется пропускать семинарские занятия по логике».
