Правила суммы и произведения
Правило суммы.Если объект А можно выбрать n способами, а объект В k способами, то объект "А или В" можно выбрать n+k способами.
Правило произведения.Если объект А можно выбрать n способами, а
объект В независимо от него k способами, то пару объектов "А и В" можно выбрать n·k способами.
Задания для самостоятельного выполнения
Задание 1.
0)В ящике находятся 20 шаров: 5 белых, 6 черных, 7 синих и 2 красных. Сколькими способами можно взять из ящика один цветной шар?
1)В розыгрыше первенства по футболу принимают участие 18 команд. Сколькими способами могут быть распределены золотая, серебряная и бронзовая медали, если любая команда может получить только одну медаль?
2)При формировании экипажа космического корабля имеется 10 претендентов на пост командира экипажа, 20 - на пост бортинженера и 25 - на пост космонавта-исследователя. Ни один кандидат не претендует одновременно на два поста. Сколькими способами можно выбрать одну из кандидатур или командира, или бортинженера, или космонавта-исследователя?
3)Сколькими способами можно выбрать на шахматной доске белый и черный квадраты, не лежащие на одной и той же горизонтали и вертикали?
4)Имеется 6 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну — на правую руку так, чтобы эти перчатки были различных размеров?
5)Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
6)В ящике лежат 4 черных и 3 белых шара. Наудачу вынимаются последовательно два шара. Какова вероятность того, что оба эти шара окажутся белыми? (Шар после выбора в ящик не возвращается.)
7)В столовой предлагают два различных первых блюда a1 и а2, три различных вторых блюда b1, b2, b3 и два вида десерта с1 и c2. Сколько различных обедов из трех блюд может предложить столовая?
8)У англичан принято давать детям несколько имен. Сколькими способами можно назвать ребенка, если общее число имен равно 300, а ему дают не более трех имен?
9)На вершину горы ведут пять дорог. Сколькими способами турист может подняться на гору и спуститься с нее? То же самое при условии, что спуск и подъем происходят по разным путям.
Размещения без повторений
Размещениями из n элементов по m (m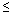 
n) называются упорядоченные m -элементные выборки из данных n элементов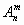 
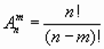
Задание 2.
0)Составьте все слова из трех букв А, В, С по две буквы.
1)В классе 30 учащихся. Сколькими способами можно выбрать из класса команду из 4 учащихся для участия в олимпиаде по истории?
2)Сколькими способами можно составить двуцветный полосатый флаг, если имеется материал 5 различных цветов? Та же задача, если одна из полос должна быть красной?
3)Из состава конференции, на которой присутствует 45 человека, надо избрать делегацию из 6 человек. Сколькими способами это можно сделать?
4)В турнире принимают участие 8 команд. Сколько различных предположений относительно распределения трех первых мест можно сделать?
5)Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различны и нечетны?
6)Сколькими способами можно сделать трехцветный флаг с горизонтальными полосами одинаковой ширины, если имеется материя 6 различных цветов?
7)Сколько существует трехзначных чисел, в записи которых цифры 1, 2, 3 встречаются ровно по одному разу?
8)На полке стоят 5 книг. Сколькими способами можно выложить в стопку несколько из них (стопка может состоять и из одной книги)?
9)У Димы есть 5 шариков: красный, зеленый, желтый, синий и золотой. Сколькими способами он сможет украсить ими 5 елок, если на каждую требуется надеть ровно один шарик?
Размещения с повторениями
Размещениями с повторениями из n по m называются упорядоченные m-элементные выборки, в которых элементы могут повторяться.
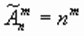
Задание 3.
0)Сколько четырехбуквенных «слов» можно составить из букв "М" и "А"?
1)Сколькими способами можно разместить восемь пассажиров в три вагона?
2)Каждый телефонный номер состоит из семи цифр. Сколько всего телефонных номеров, не содержащих других цифр, кроме 2, 3, 5 и 7?
3)Четверо студентов сдают экзамен. Сколькими способами могут быть поставлены им отметки, если известно, что никто из них не получил неудовлетворительной отметки?
4)Сколько различных трехбуквенных слов можно составить из 32 букв алфавита (со смыслом и без)?
5)В селении проживает 2000 жителей. Доказать, что, по крайней мере, двое из них имеют одинаковые инициалы.
6)Сколькими способами можно покрасить пять елок в серебристый, зеленый и синий цвета, если количество краски неограниченно, а каждую елку можно покрасить только в один цвет?
7)Каждую клетку квадратной таблицы 2 × 2 можно покрасить в черный или белый цвет. Сколько существует различных раскрасок этой таблицы?
8)Сколькими способами можно заполнить одну карточку в лотерее «Спортпрогноз»'? Указание: в этой лотерее нужно предсказать итог тринадцати спортивных матчей. Итог каждого матча - победа одной из команд либо ничья; счет роли не играет.
9)Алфавит племени Мумбо-Юмбо состоит из трех букв А, Б и В. Словом является любая последовательность, состоящая не более, чем из 4 букв. Сколько слов в языке племени Мумбо-Юмбо? Указание: сосчитайте отдельно количества одно-, двух-, трех- и четырехбуквенных слов.