Научная и инженерная графика
Функция plot имеет различные формы, связанные с входными параметрами.
Пример 1. Построение графика значений функции sin от нуля до 2 с шагом 0,01.
>> x=0:0.01:2;
y=sin(x);
plot(x,y)
Полученный в окне Figure № 1 график может быть перенесен в отчетный документ при помощи опции Edit→Copy Figure (рис. 11).
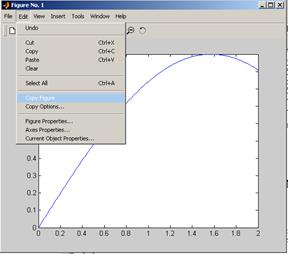
Рис. 11
Пример 2. Построение нескольких графиков значений функции sin от нуля до 2π.
>> x=0: pi/10: 2*pi;
y=sin(x); y2=0.6*sin(x-0.25); y3=0.8*sin(x-0.5);
plot(x,y, x,y2, 'b:*', x,y3, 'm:+')
Входные данные для plot обеспечивают построение цветных пунктирных графиков и помещают маркеры «+» и «*» в каждую точку данных (рис. 12).
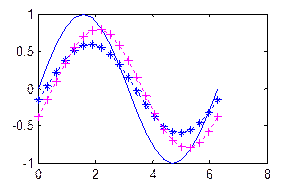
Рис 12
Пример 3. Построение графиков функций в разных окнах.
>> x=0: 0.01: 2;
>> y1=sin(x); y2=cos(x);
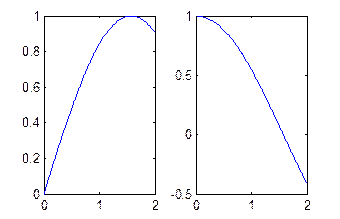 >> plot(x,y1)
>> plot(x,y1)
>> hold on
>> subplot(1,2,1);
>> plot(x,y1)
>> subplot(1,2,2);
>> plot(x,y2)
Рис. 13
Пример 4. Построение трехмерных графиков функций.
Для отображения функции двух переменных следует:
1. Сгенерировать матрицы с координатами узлов сетки.
2. Вычислить функцию в узлах сетки.
3. Использовать одну из графических функций.
Соответственно этим пунктам написана программа.
>> [X,Y]=meshgrid(-1: 0.05: 1, 0: 0.05: 1);
>> Z=4*sin(2*pi*X).*cos(1.5*pi*Y).*(1-X.^2).*Y.*(1-Y);
>> mesh(X,Y,Z);
>> surf(X,Y,Z); colorbar
Функция surf строит каркасную поверхность графика функции и заливает каждую клетку поверхности определенным цветом. Для удобства масштабирования рядом с графиком выводится столбик, устанавливающий соответствие между цветом и значением функции colorbar.
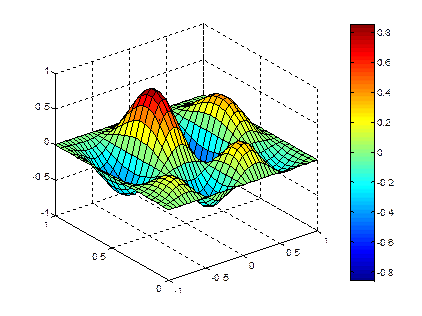
Рис. 14
Лабораторная работа 3
Вычислительный эксперимент, программирование,
Разработка приложений
Выполнение команд, содержащихся в M-файле, осуществляется двумя способами:
1. Из редактора M-файлов (клавиша F5).
2. Из командной строки или другого M-файла, при этом в качестве команды используется имя M-файла.
Первый способ рекомендуется при отладке программы. Применение второго способа намного удобнее, особенно, если созданный M-файл будет неоднократно использоваться впоследствии. Закройте все окна и наберите в командной строке fun2. Появится графическое окно с результатом.
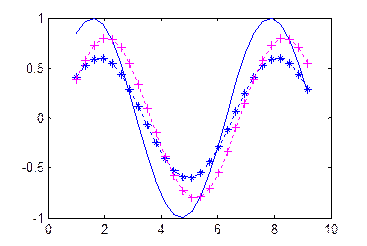 Пример 1. Программа для построения рис. 13 записана в M-файл с именем graf1.m. Для интервала исследования
Пример 1. Программа для построения рис. 13 записана в M-файл с именем graf1.m. Для интервала исследования
>>x=1: pi/10: 3*pi; graf1(x) получен график (рис. 15).
function y=graf1(x)
y=sin(x);
y2=0.6*sin(x-0.25);
y3=0.8*sin(x-0.5);
plot(x,y, x,y2, 'b:*', x,y3, 'm:+')
Рис. 15
Пример 2. Программа для построения рис. 12 записана в M-файл с именем graf.m. Причем интервал исследования для переменной теперь стал входным параметром программы:
function y=graf(x)
title('{\itf(x)=x^{n}}');
xlabel('x');
ylabel('y');
hFigure=gcf;
set(hFigure,'Color',[1 1 1]);
hText=text;
set(hText,'FontSize',[18]);
for n=2:4
y=x.^n;
hold on
hPlot=plot(x,y);
set(hPlot,'Color',[1.8/n 0.7 0.5]);
set(hPlot,'LineWidth',2);
if n~=2
for i=1:length(y)
s='';
if y(i)==y1(i)
hold on
plot(x(i),y(i),'ko');
s=['(' num2str(x(i)) ',' num2str(y(i)) ')'];
hText=text(x(i),y(i)+2, s); set(hText,'FontSize',[16]);
end
end
end
y1=y; s2=['n=' num2str(n)];
hText=text(1.5, 1.5^2*n-1, s2); set(hText,'FontSize',[14]);
end
Теперь можно построить график функции в другом интервале изменения параметра x. После выполнения команды x=-3: 0.1: 2.5; graf(x) построен график (рис. 15).
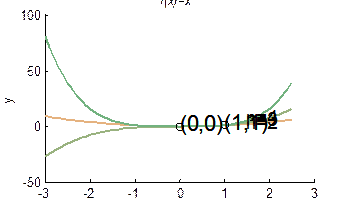
Рис. 15
Лабораторная работа 4
