Базовые логические элементы

Математическая логика тесно связана с теорией проектирования ЭВМ. Поведение различных компонентов ЭВМ может быть описано с помощью логических функций и законов математической логики. Кроме того, современные языки программирования просто не мыслимы без встроенных в них логических функций.

Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию.Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.

Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ, триггер и другие.

С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера.

Работу логических элементов описывают с помощью таблиц истинности.

Схема И,реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах схемы И с двумя входами представлено на рисунке 3.4.1.

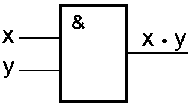Рисунок 3.4.1. – Логическая схема И.

Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Если хотя бы на одном входе будет ноль, на выходе также будет ноль.

Схема ИЛИ, реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы ИЛИ будет единица, на её выходе также будет единица.

Условное обозначение на структурных схемах схемы ИЛИ с двумя входами представлено на рисунке 3.4.2.

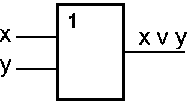Рисунок 3.4.2. – Логическая схема ИЛИ.

Схема НЕ (инвертор) – реализует операцию отрицания. Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0. Условное обозначение на структурных схемах инвертора – на рисунке 3.4.3.

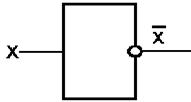Рисунок 3.4.3. – Логическая схема НЕ.

Схема И–НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И. Условное обозначение на структурных схемах схемы И–НЕ с двумя входами представлено на рисунке 21.4.4.

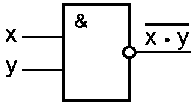Рисунок 3.4.4. – Логическая схема И–НЕ.

Схема ИЛИ—НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Условное обозначение на структурных схемах схемы ИЛИ—НЕ с двумя входами представлено на рисунке 3.4.5.

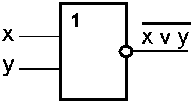Рисунок 3.4.5. – Логическая схема ИЛИ–НЕ.

Пример 3.4.1.Дана логическая схема с двумя входами (рисунок 3.4.6). На один вход подается сигнал X, а на другой – сигнал Y. Запишите в серые клетки логической схемы поэтапные значения работы.

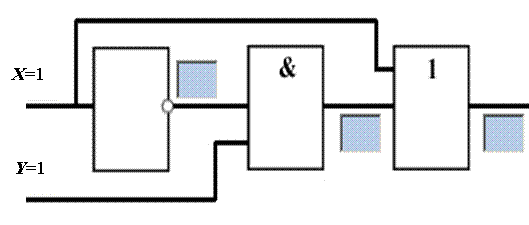Рисунок 3.4.6 – Логическая схема

На вход Х подается 1, проходя через инвертор 1 преобразуется в 0, следовательно, в первой левой клетке появится 0. Далее на схему И подается 0 из инвертора и 1 (сигнал Y) в результате 1&0=0 (0 записывается во второй серой ячейке). На вход схемы ИЛИ поступает 0 со схемы И и 1(сигнал X). 0V1=1. На выходе общей схемы получаем 1, при исходных данных Х=1 и Y=1.

Пример 3.4.2.Дана логическая схема с двумя входами (рисунок 3.4.6), Эту схему необходимо описать соответствующей логической функцией.

Построим логическую функцию, которая описывает исходную схему:

– сигнал X проходит через инвертор и преобразуется в Х;

– на схему И приходит Х и Y, на выходе имеем Х &Y;

– полученный на предыдущем шаге сигнал Х&Y и сигнал Х, подаются на схему ИЛИ, в результате чего получаем выходной итоговый сигнал. Он описывается логической формулой (Х&Y)VХ.

Пример 3.4.3.Построить логическую схему для логической функции

Q = (Х V Y) & Х. Поэтапное построение логической схемы отобразим в таблице 3.4.1.

Таблица 3.4.1 – Построение логической схемы для функции Q.

№ п/п	Этапы построения
	Сигнал Y необходимо инвертировать, чтобы получить Y. Для этого сигнал Y пропускаем через инвертор.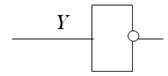
	Далее сигналы Х и Y передаём на схему ИЛИ (реализуем операцию Х V Y)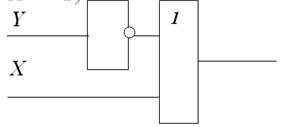
	Полученный на втором этапе сигнал и сигнал Х подаем на схему И (реализуем операцию (Х V Y) & Х). 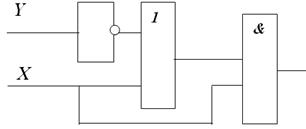Логическая схема для функции Q построена.

Триггер– это электронная схема, широко применяемая в регистрах компьютера для надёжного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю.

Термин триггер происходит от английского слова trigger — защёлка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает “хлопанье”. Это звукоподражательное название электронной схемы указывает на её способность почти мгновенно переходить (“перебрасываться”) из одного электрического состояния в другое и наоборот.

Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта, соответственно, 8 х 2¹⁰ = 8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.

Сумматор ­– это электронная логическая схема, выполняющая суммирование двоичных чисел.

Сумматор служит, прежде всего, центральным узлом арифметико-логического устройства компьютера, однако он находит применение также и в других устройствах машины.

Сумматоры бывают одноразрядные и многоразрядные.

Одноразрядный двоичный сумматор этоь устройство с тремя входами и двумя выходами. Условное обозначение одноразрядного сумматора изображено на рисунке 3.4.7.

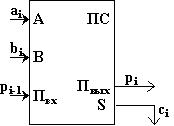Рисунок 3.4.7. – Логическая схема сумматора.

Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров.

При сложении чисел A и B в одном i-ом разряде приходится иметь дело с тремя цифрами:

– цифра ai, первого слагаемого;

– цифра bi, второго слагаемого;

– перенос pi–1 из младшего разряда.

В результате сложения получаются две цифры:

– цифра ci для суммы;

– перенос pi из данного разряда в старший.

Следует отметить, что при работе с двоичными числами, любую операцию можно представить как производную суммирования.