Постулаты теории измерений
Понятие об измерении
Метрология (от греч. «метро» – мера, «логос» – учение) – наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности измерений.
К ключевым понятиям законодательной метрологии относят:
измерение; физическую величину; средство измерений; эталон и меру; рабочее и образцовое СИ (ОСИ); измерительный преобразователь и датчик; метод и алгоритм измерений; методику выполнения измерений; метрологическую аттестацию СИ; поверку СИ; испытания СИ, метрологический надзор; сертификация СИ, ГСИ и др.
Предмет метрологии – извлечение количественной информации о свойствах объектов и процессов, т. е. измерение свойств объектов и процессов с заданной точностью и достоверностью. Важнейшая задача метрологии – обеспечение единства измерений – решается при соблюдении двух условий: выражение результатов измерений в узаконенных единицах и установление допускаемых погрешностей результатов измерений и границ, за которые они не должны выходить при заданной вероятности. Погрешности измерений указываются в паспорте, ТУ и иной нормативной документации,
касающейся средства измерения.
Измерение – это нахождение значения физической величины опытным путем с помощью специальных технических средств. Измерение физической величины включает совокупность операций по применению технического средства, хранящего единицу ФВ или воспроизводящего шкалу ФВ, заключающихся в сравнении измеряемой величины с ее единицей или шкалой с целью получения значения этой величины в форме, удобной для использования. Найденные значения называют результатом измерений. Измерительная информация – информация о значениях измеряемых ФВ. Она может быть представлена в формах: аналоговой, цифровой или панорамной (в виде графиков). Сигнал измерительной информации – это сигнал, функционально связанный с измеряемой ФВ.
Измерение - это нахождение значения физической величины опытным путем с помощью специальных технических средств
Средства измерений - это технические средства, которые имеют нормированные метрологические характеристики. При этом значение физической величины, отсчитываемое поотсчетному устройству средства измерения, строго соответствует определенному количеству физических единиц, принятых в качестве единиц измерения.
Эталон - средство измерений, обеспечивающее воспроизведение и хранение единицы физической величины для передачи ее размера средствам измерения, нижестоящим по поверочной схеме.
Физические величины разделяют на измеряемые и оцениваемые. Измеряемые величины могут быть выражены количественно в установленных единицах измерения. Величины, для которых не может быть введена единица измерения, относятся к оцениваемым. Оценку величины проводят при помощи установленной шкалы
Постулаты теории измерений
Первым постулатом метрологии является постулат α: в рамках принятой модели объекта исследования существует определенная измеряемая физическая величина и ее истинное значение. Если, например, считать, что деталь представляет собой цилиндр (модель — цилиндр), то она имеет диаметр, который может быть измерен. Если же деталь нельзя считать цилиндрической, например ее сечение представляет собой эллипс, то измерять ее диаметр бессмысленно, поскольку измеренное значение не несет полезной информации о детали. И, следовательно, в рамках новой модели диаметр не существует. Измеряемая величина существует лишь в рамках принятой модели, т. е. имеет смысл только до тех пор, пока модель признается адекватной объекту. Так как при различных целях исследований данному объекту могут быть сопоставлены различные модели, то из постулата а вытекает следствие α1: для данной физической величины объекта измерения существует множество измеряемых величин (и соответственно их истинных значений).
Итак, из первого постулата метрологии следует, что измеряемому свойству объекта измерений должен соответствовать некоторый параметр его модели. Данная модель в течение времени, необходимого для измерения, должна позволять считать этот ее параметр неизменным. В противном случае измерения не могут быть проведены. Указанный факт описывается постулатом β:истинное значение измеряемой величины постоянно.
Выделив постоянный параметр модели, можно перейти к измерению соответствующей величины. Для переменной ФВ необходимо выделить или выбрать некоторый постоянный параметр и измерить его. В общем случае такой постоянный параметр вводится с помощью некоторого функционала. Примером таких постоянных параметров переменных во времени сигналов, вводимых посредством функционалов, являются средневыпрямленные или среднеквадратические значения. Данный аспект отражается в следствии β1: для измерения переменной физической величины необходимо определить ее постоянный параметр — измеряемую величину.
При построении математической модели объекта измерения неизбежно приходится идеализировать те или иные его свойства. Модель никогда не может полностью описывать все свойства объекта измерений. Она отражает с определенной степенью приближения некоторые из них, имеющие существенное значение для решения данной измерительной задачи. Модель строится до измерения на основе априорной информации об объекте и с учетом цели измерения. Измеряемая величина определяется как параметр принятой модели, а его значение, которое можно было бы получить в результате абсолютно точного измерения, принимается в качестве истинного значения данной измеряемой величины. Эта неизбежная идеализация, принятая при построении модели объекта измерения, обуславливает неизбежное несоответствие между параметром модели и реальным свойством объекта, которое называется пороговым. Принципиальный характер понятия "пороговое несоответствие" устанавливается постулатом γ: существует несоответствие измеряемой величины исследуемому свойству объекта (пороговое несоответствие измеряемой величины).Пороговое несоответствие принципиально ограничивает достижимую точность измерений при принятом определении измеряемой ФВ.
Изменения и уточнения цели измерения, в том числе и такие, которые требуют повышения точности измерений, приводят к необходимости изменять или уточнять модель объекта измерений и переопределять понятие измеряемой величины. Основной причиной переопределения является то, что пороговое несоответствие ранее принятого определения не позволяет повысить точность измерения до уровня требуемой. Вновь введенный измеряемый параметр модели также может быть измерен лишь с погрешностью, которая в лучшем случае равна погрешности, обусловленной пороговым несоответствием. Поскольку принципиально невозможно построить абсолютно адекватную модель объекта измерения, то нельзя устранить пороговое несоответствие между измеряемой ФВ и описывающим ее параметром модели объекта измерений. Отсюда вытекает важное следствие γ1: истинное значение измеряемой величины отыскать невозможно.
Модель можно построить только при наличии априорной информации об объекте измерения. При этом чем больше информации, тем более адекватной будет модель и соответственно точнее и правильнее будет выбран ее параметр, описывающий измеряемую ФВ. Следовательно, увеличение априорной информации уменьшает пороговое несоответствие. Данная ситуация отражается в следствии γ2: достижимая точность измерения определяется априорной информацией об объекте измерения.
Из этого следствия вытекает, что при отсутствии априорной информации измерение принципиально невозможно. В то же время максимально возможная априорная информация заключается в известной оценке измеряемой величины, точность которой равна требуемой. В этом случае необходимости в измерении нет.
В заключение подчеркнем, что приведенные постулаты и их следствия являются лишь одной из попыток построить теоретический фундамент метрологии и их не следует считать истиной в конечной инстанции.
3. Элементы процесса измерения
Элементы процесса измерений
Измерение — сложный процесс, включающий в себя взаимодействие целого ряда его структурных элементов. К ним относятся: измерительная задача, объект измерения, принцип, метод и средство измерения и его модель, условия измерения, субъект измерения, результат и погрешность измерения. Эти элементы и их взаимосвязи показаны на рис. 2.5 в виде структурной схемы. Из нее видно, что процесс измерения протекает по двум параллельным ветвям, содержащим соответствующие друг другу элементы, относящиеся к реальности (верхняя ветвь) и ее отражению, или познанию (нижняя ветвь). Элементы обеих ветвей, неразрывно связанных между собой, соответствуют друг другу по типу "реальность — отражение (модель)".
Первым начальным элементом каждого измерения является его задача (цель).Задача любого измерения заключается в определении значения выбранной (измеряемой) ФВ с требуемой точностью в заданных условиях. Постановку задачи измерения осуществляет субъект измерения — человек. При постановке задачи конкретизируется объект измерения, в нем выделяется измеряемая ФВ и определяется (задается) требуемая погрешность измерения.
Объект измерения — это реальный физический объект, свойства которого характеризуются одной или несколькими измеряемыми ФВ. Он обладает многими свойствами (Св1 ..., Свi, см. рис. 2.5) и находится в многосторонних и сложных связях с другими объектами. Субъ ект измерения — человек принципиально не в состоянии представить себе объект целиком, во всем многообразии его свойств и связей. Вследствие этого взаимодействие субъекта с объектом возможно только на основе математической модели объекта.
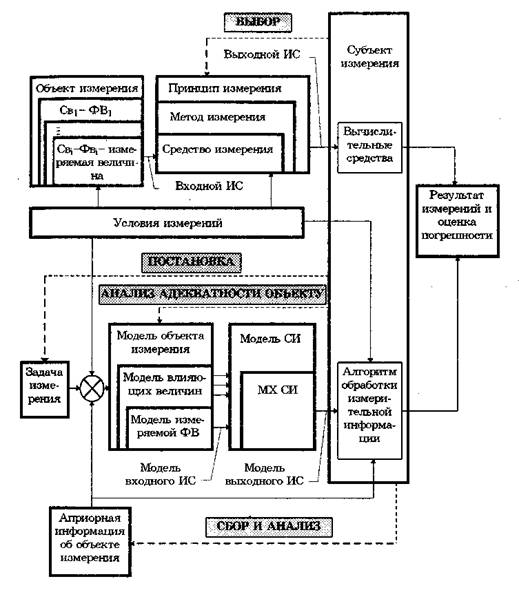
Рис. 2.5. Основные элементы процесса измерения:
СИ — средство измерений, MX — метрологические характеристики,
ИС — измерительный сигнал, ФВ — физическая величина, Св — свойство
Математическая модель объекта измерения — это совокупность математических символов (образов) и отношений между ними, которая адекватно описывает интересующие субъекта свойства объекта измерения.
Модель объекта измерения строится до выполнения измерения в соответствии с решаемой задачей на основе априорной информации об объекте и условиях измерения. На рис. 2.5 это отражено в виде суммирования сведений о цели, условиях измерения и априорной информации об объекте. Модель объекта измерения должна удовлетворять следующим требованиям:
• погрешность, обусловленная несоответствием модели объекту измерения, не должна превышать 10% предельно допускаемой погрешности измерения;
• составляющая погрешности измерения, обусловленная нестабильностью измеряемой ФВ в течение времени, необходимого для проведения измерения, не должна превышать 10% предельно допускаемой погрешности.
Если выбранная модель не удовлетворяет этим требованиям, то следует перейти к другой модели объекта измерений.
Априорная информация, т.е. информация об объекте измерения, известная до проведения измерения, является важнейшим фактором, обуславливающим его эффективность. При полном отсутствии этой информации измерение в принципе невозможно, так как неизвестно, что же необходимо измерить, а следовательно, нельзя выбрать нужные средства измерений. При наличии априорной информации об объекте в полном объеме, т.е. при известном значении измеряемой величины, измерения попросту не нужны. Указанная информация определяет достижимую точность измерений и их эффективность.
Измеряемая величина определяется как параметр принятой модели, а ее значение, которое можно было бы получить в результате абсолютно точного эксперимента, принимается в качестве истинного значения данной величины. Идеализация, принятая при построении модели объекта измерения, обуславливает несоответствие параметра модели исследуемому свойству объекта. Это несоответствие называют пороговым..Обычно на практике из-за трудности оценивания пороговое несоответствие стремятся сделать пренебрежимо малым. ^
Цель построения модели объекта измерения состоит в выявлении (представлении) конкретной ФВ, подлежащей определению. Собственно следует говорить не о модели объекта измерения в делом, а о модели его измеряемого свойства или измеряемой ФВ.
Модель объекта измерения необязательно должна быть математической. Ее характер должен определяться видом и свойствами объекта измерений, а также целью измерений. Моделью может служить любое приближенное описание объекта, которое позволяет выделить параметр модели (или функционал параметров), являющийся измеряемой величиной и отражающий то свойство объекта измерений, которое необходимо оценить для решения измерительной задачи. Модель должна достаточно хорошо отражать две группы свойств (ФВ) объекта измерений: определяемые при измерении и влияющие на результат измерения.
Основной проблемой моделирования объектов измерений является выбор таких моделей, которые можно считать адекватно описывающими измеряемые величины (свойства) данного объекта. Важно отметить, что адекватность модели обуславливается не только теми свойствами объекта, которые требуется определить в рамках данной измерительной задачи, но и теми, которые могут влиять на результаты измерения искомой величины.
Построение адекватных моделей объектов измерений до настоящего времени является сложной творческой и неформализуемой задачей. Ее решение требует высокой квалификации, опыта и, естественно, инженерной интуиции. При этом зачастую приходится решать две взаимоисключающие задачи: модель должна адекватно отражать все свойства объекта, необходимые для решения измерительной задачи, и в то же время быть по возможности простой и содержать минимум параметров.
В большинстве практических инженерных задач модели объектов намерений достаточно очевидны и, как правило, несложны. Объект измерения характеризуется набором свойств и описывающих их ФВ. На рис. 2.5 одна из них (i-я) является измеряемой величиной. Измеряемая величина — это ФВ, подлежащая определению в соответствии с измерительной задачей. До недавнего времени понятие "физическая величина" считалось достаточным для постановки и решения всех измерительных задач. Однако из-за существенного расширения области применения измерений, усложнения их задач и усиления требований к точности и достоверности в ряде случаев оно перестало удовлетворять потребности в экспериментальном определении различных свойств разнообразных объектов.
При планировании современных измерений требуется введение более конкретных понятий, определяемых целями измерений, чем весьма общего понятия "физическая величина". В настоящее время под измеряемой величиной понимается параметр или функционал параметра модели объекта измерений, отражающий то его свойство, количественную оценку которого необходимо получить в результате измерений. Измеряемая величина всегда имеет размерность определенной ФВ, но представляет собой некоторую ее конкретизацию, обусловленную свойствами объекта измерений, которые связаны с поставленной целью измерений.
4. Этапы измерения
2.4. Основные этапы измерений
Измерение — последовательность сложных и разнородных действий, состоящая из ряда этапов [24]. Первым этапом любого измерения является постановка измерительной задачи. Он включает в себя:
• сбор данных об условиях измерения и исследуемой ФВ, т.е. накопление априорной информации об объекте измерения и ее анализ;
• формирование модели объекта и определение измеряемой величины, что является наиболее важным, особенно при решении сложных измерительных задач. Измеряемая величина определяется с помощью принятой модели как ее параметр или характеристика. В простых случаях, т.е. при измерениях невысокой точности, модель объекта в явном виде не выделяется, а пороговое несоответствие пренебрежимо мало;
• постановку измерительной задачи на основе принятой модели объекта измерения;
• выбор конкретных величин, посредством которых будет находиться значение измеряемой величины;
• формулирование уравнения измерения.
Вторым этапом процесса измерения является планирование измерения. В общем случае оно выполняется в следующей последовательности:
• выбор методов измерений непосредственно измеряемых величин и возможных типов СИ;
• априорная оценка погрешности измерения;
• определение требований к метрологическим характеристикам СИ и условиям измерений;
• выбор СИ в соответствии с указанными требованиями;
• выбор параметров измерительной процедуры (числа наблюдений для каждой измеряемой величины, моментов времени и точек выполнения наблюдений);
• подготовка СИ к выполнению экспериментальных операций;
• обеспечение требуемых условий измерений или создание возможности их контроля.
Эти первые два этапа, являющиеся подготовкой к измерениям, имеют принципиальную важность, поскольку определяют конкретное содержание следующих этапов измерения. Подготовка проводится на основе априорной информации. Качество подготовки зависит от того, в какой мере она была использована. Эффективная подготовка является необходимым, но недостаточным условием достижения цели измерения. Ошибки, допущенные при подготовке измерений, с трудом обнаруживаются и корректируются на последующих этапах.
Третий, главный этап измерения — измерительный эксперимент. В узком смысле он является отдельным измерением. В общем случае последовательность действий во время этого этапа следующая:
• взаимодействие средств и объекта измерений;
• преобразование сигнала измерительной информации;
• воспроизведение сигнала заданного размера;
• сравнение сигналов и регистрация результата. Последний этап измерения —обработка экспериментальных
данных. В общем случае она осуществляется в последовательности, которая отражает логику решения измерительной задачи:
• предварительный анализ информации, полученной на предыдущих этапах измерения;
• вычисление и внесение возможных поправок на систематические погрешности;
• формулирование и анализ математической задачи обработки данных;
• построение или уточнение возможных алгоритмов обработки данных, т.е. алгоритмов вычисления результата измерения и показателей его погрешности;
• анализ возможных алгоритмов обработки и выбор одного из них на основании известных свойств алгоритмов, априорных данных и предварительного анализа экспериментальных данных;
• проведение вычислений согласно принятому алгоритму, в итоге которых получают значения измеряемой величины и погрешностей измерений;
• анализ и интерпретация полученных результатов;
• запись результата измерений и показателей погрешности в соответствии с установленной формой представления.
Некоторые пункты данной последовательности могут отсутствовать при реализации конкретной процедуры обработки результатов измерений.
Задача обработки данных подчинена цели измерения и после выбора СИ однозначно вытекает из измерительной задачи и, следовательно, является вторичной. Подробно обработка результатов измерений различных типов рассмотрена в гл. 8.
Перечисленные выше этапы существенно различаются по выполняемым операциям и их трудоемкости. В конкретных случаях соотношение и значимость каждого из этапов заметно варьирует. Для многих технических измерений вся процедура измерения сводится к экспериментальному этапу, поскольку анализ и планирование, включая априорное оценивание погрешности, выбор нужных методов и средств измерений осуществляются предварительно, а обработка данных измерений, как правило, минимизируется.
Выделение этапов измерения имеет непосредственное практическое значение — способствует своевременному осознанному выполнению всех действий и оптимальной реализации измерений. Это в свою очередь позволяет избежать серьезных методических ошибок, связанных с переносом проблем одного этапа на другой.
5. Классификация измерений
Классификация средств измерений может проводиться по следующим критериям.
1. По характеристике точности измерения делятся на равноточные и неравноточные.
Равноточными измерениями физической величины называется ряд измерений некоторой величины, сделанных при помощи средств измерений (СИ), обладающих одинаковой точностью, в идентичных исходных условиях.
Неравноточными измерениями физической величины называется ряд измерений некоторой величины, сделанных при помощи средств измерения, обладающих разной точностью, и (или) в различных исходных условиях.
Равноточные измерения— определенное количество измерений любой величины, произведенных аналогичными по точности средствами измерений в одинаковых условиях.
Неравноточные измерения— определенное количество измерений любой величины, произведенных отличными по точности средствами измерений и (или) в различных условиях.
2. По количеству измерений измерения делятся на однократные и многократные.
Однократное измерение— измерение, произведенное один раз.
Многократное измерение— измерение одного размера величины, результат этого измерения получают из нескольких последующих однократных измерений (отсчетов).
3. По типу изменения величины измерения делятся на статические и динамические.
Статические измерения — это измерения постоянной, неизменной физической величины.
Динамические измерения — это измерения изменяющейся, непостоянной физической величины.
Динамическое измерение— измерение величины, размер которой изменяется с течением времени. Быстрое изменение размера измеряемой величины требует ее измерения с точнейшим определением момента времени. Например, измерение расстояния до уровня поверхности Земли с воздушного шара или измерение постоянного напряжения электрического тока. По существу динамическое измерение является измерением функциональной зависимости измеряемой величины от времени.
Статическое измерение— измерение величины, которая принимается всоответствии с поставленной измерительной задачей за неизменяющуюся на протяжении периода измерения.
4. По предназначению измерения делятся на технические и метрологические.
Технические измерения — это измерения, выполняемые техническими средствами измерений.
Метрологические измерения — это измерения, выполняемые с использованием эталонов.
Технические измерения— измерения с целью получения информациио свойствах материальных объектов, процессов и явлений окружающего мира.
Метрологические измерения— измерения для реализации единства и необходимой точности технических измерений.
5. По способу представления результата измерения делятся на абсолютные и относительные.
Абсолютные измерения — это измерения, которые выполняются посредством прямого, непосредственного измерения основной величины и (или)
применения физической константы.
Относительные измерения — это измерения, при которых вычисляется отношение однородных величин, причем числитель является сравниваемой величиной, а знаменатель — базой сравнения (единицей).
Относительное измерение— измерение отношения величины к одноименной величине, занимающее место единицы. Например, относительным измерением является определение активности радионуклида в источнике методом измерения ее отношения к активности радионуклида в ином источнике, аттестованном как эталонная мера величины.
Абсолютное измерение - это измерение, основанное на прямых измеренияходной или нескольких основных величии и (или) использовании значений фундаментальных физических констант.
6. По методам получения результатов измерения делятся на прямые, косвенные, совокупные и совместные.
Прямые измерения — это измерения, выполняемые при помощи мер, т. е. измеряемая величина сопоставляется непосредственно с ее мерой. Примером прямых измерений является измерение величины угла (мера — транспортир).
Косвенные измерения — это измерения, при которых значение измеряемой величины вычисляется при помощи значений, полученных посредством прямых измерений.
Совокупные измерения — это измерения, результатом которых является решение некоторой системы уравнений. Совместные измерения — это измерения, в ходе которых измеряется минимум две неоднородные физические величины с целью установления
существующей между ними зависимости.
прямое измерение— это измерение, проведенное при помощи средства измерений, хранящего единицу или шкалу измеряемой величины. Как пример, измерение длины изделия штангенциркулем, электрического напряжения вольтметром и т.п.
Косвенное измерение— измерение, когда значение величины определяют на основании результатов прямых величин, функционально связанных с искомой.
Совокупные измерения — когда проводят измерения одновременнонескольких однородных величин, когда значения этих величин находят путем решения системы уравнений, получаемых при измерениях различных сочетаний этих величин.
Классический пример совокупных измерений — калибровка набора гирь по одной эталонной гире, проводимая путем измерений различных сочетаний гирь этого набора,и решения полученных уравнений.
Совместные измерения — проводимые одновременно измерения двух или нескольких разнородных величин для определения зависимости между ними.
Другими словами, совместные измерения — это измерения зависимостей между величинами.
6. Понятие о средствах измерения. Характеристики средств измерения
Средства измерений - это технические средства, которые имеют нормированные метрологические характеристики. При этом значение физической величины, отсчитываемое поотсчетному устройству средства измерения, строго соответствует определенному количеству физических единиц, принятых в качестве единиц измерения.
Характеристики средств измерений
Метрологическая характеристика средства измерений — характеристика одного из свойств средства измерений, влияющая на результат измерений и на его погрешности. От точности характеристик при изготовлении средств измерений, стабильности их в процессе эксплуатации зависит точность результатов измерений. Для каждого типа средств измерений устанавливают свои метрологические характеристики в зависимости от назначения, условий эксплуатации и других факторов.
Метрологические характеристики, устанавливаемые нормативно-техническими документами, называются нормируемыми метрологическими характеристиками, а определяемые экспериментально — действительными метрологическими характеристиками. Предлагаемые характеристики относятся к приборам, предназначенным для осуществления измерений.
Градуировочная характеристика — зависимость между значениями величин X на входе и У на выходе средств измерений, полученная экспериментально:
У = f(X)
Градуировочная характеристика может быть выражена в виде формулы, графика или таблицы. Она связывает конструктивные параметры прибора с величинами X и У.
Номинальная градуировочная характеристика — это характеристика при нормальных условиях внешней среды и неизменных или медленно изменяющихся значениях входного сигнала.
Чувствительность прибора — свойство, определяемое отношением изменения выходного сигнала прибора к вызывающему его изменению измеряемой величины.
Абсолютная чувствительность
S = ∆У/∆Х,
где ∆У и ∆Х — изменение соответственно сигнала на выходе и измеряемой величины.
Относительная чувствительность
Sо = ∆У/(∆Х/Х),
где ∆Х/Х — относительное изменение измеряемой величины.
Пороз чувствительности — характеристика прибора а виде наименьшего значения изменения величины, начиная с которого может осуществляться ее измерение данным прибором.
Шкала прибора — часть показывающего устройства прибора, представляющая собой упорядоченный ряд отметок вместе со связанной с ними нумерацией.
Числовая отметка шкалы — число, соответствующее некоторому значению физической величины:
С = ∆Х /∆У =1/S.
Цена деления школы — разность значений величины, соответствующих двум соседним отметкам шкалы прибора.
Цена деления и чувствительность — величины именованные. Обычно говорят о чувствительности прибора к какой-то измеряемой величине (напряжению, току, сопротивлению и т. д.). Например, S = 5 дел. /В; С = 0,2 В/дел.
Показание прибора — значение величины или число на показывающем устройстве прибора.
Вариация показаний прибора — разность показаний прибора в одной и той же точке диапазона измерений при плавном подходе к этой точке со стороны меньших и больших значений измеряемой величины.
Диапазон измерений прибора — область значений величины, в пределах которой нормированы допускаемые пределы погрешности прибора. Эта область ограничена нижним и верхним пределами измерений. Диапазон измерений может состоять из нескольких поддиапазонов с разными погрешностями. Диапазон показаний может не совпадать с диапазоном измерений, под которым понимается область значений, ограниченная начальным и конечным значениями шкалы.
Входные и выходные характеристики ИП соответственно определяют воздействия ИП на объект исследования. При подключении средств измерений к объекту измерения вследствие их взаимного влияния могут возникнуть погрешности. В частности, средства измерения потребляют некоторую мощность от объекта измерения (источника входного сигнала), что приводит к изменению режима работы объекта измерения, если объект маломощный. Малое потребление мощности от источника входного сигнала является достоинством средств измерения, которым обладают электронные приборы. Выходные характеристики определяют реакцию выходного сигнала на подключение нагрузки.
Вид выходного кода — число разрядов кода (цена единицы наименьшего разряда кода ИП), предназначенное для выдачи результатов в цифровом виде.
Область рабочих частот — полоса частот, в пределах которой погрешность прибора, вызванная изменением частоты, не превышает допускаемого предела.
Быстродействие — время, затрачиваемое на одно измерение. Для аналоговых приборов быстродействие определяется временем установления показаний (временем успокоения), т. е. промежутком времени с момента изменения измеряемой величины до момента установления показаний прибора. Для цифровых приборов быстродействие определяется как отношение числа измерений за некоторый промежуток времени к этому промежутку времени: В = п/∆t. Быстродействие цифровых приборов составляет от одного до десятков тысяч измерений в секунду и более.
Кроме метрологических характеристик при эксплуатации необходимо учитывать:
надежность средств измерений, т. е. способность приборов сохранять эксплуатационные параметры в установленных пределах в течение заданного времени. К основным критериям надежности относятся вероятность безотказной работы в течение заданного времени, интенсивность отказов, среднее время безотказной работы. Надежность прибора оценивается в процессе его разработки;
экономичность средств измерений — простота конструкций в обращении и оправданная экономическая стоимость.
