Свойства рядов предпочтительных чисел

Ряды ПЧ обладают свойствами геометрической прогрессии.

Ряды ПЧ не ограничиваются в обоих направлениях, при этом числа менее 1,0 и более 10 получают делением или умножением на 10, 100 и т.д. За исходный ряд принимают члены прогрессии, расположенные в интервале от 1,0 до 10.

Число 1,0 обязательно имеющееся в ряду, не входит в десятичный интервал 1,0<a≤10. Его следует рассматривать как завершающее число предыдущего десятичного интервала 0,1<а≤1,0.

Порядковые номера чисел представляют собой основание ряда, умноженное на десятичный логарифм числа ряда.

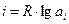
Найти номер ПЧ можно еще одним способом:

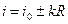
где i₀ - номер числа в нулевом интервале (1.0 <а ≤ 10 );

k - целое положительное или отрицательное число, определяющее удаление рассматриваемого интервала в ту или другую сторону от нулевого (количество раз, на которое необходимо умножить или поделить на 10 наше число, чтобы получить табличное. Если делили на 10, то знак в формуле плюс, если умножали то минус);

R - число значений ПЧ в десятичном интервале (номер ряда).

Пример: найти № ПЧ 0,025 ряд R5.Данному числу соответствует k=-2.

По таблице ПЧ находим числа в нулевом интервале i₀=2, тогда из формулы имеем:

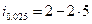
Второй способ: .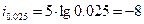

Нахождение номера ряда можно осуществлять, используя определения определение знаменателя ряда:

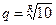
Прологарифмируем:

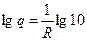, следовательно .

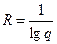Пример: известен знаменатель q=1.25, необходимо найти номер ряда:

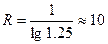, следовательно, R=10.

Для упрощения расчетов по взаимосвязанным показателям стандартов используется известное свойство логарифмов, позволяющее вместо умножения или деления самих ПЧ соответственно складывать или вычитать номера этих чисел и по результирующему номеру определять искомое число. Возведение предпочтительного числа в целую положительную или отрицательную степень производят путем умножения номера предпочтительного числа на показатель степени и по полученному номеру находят соответствующее число в таблице. При этом удается, кроме ускорения вычислений, не оперировать округленными значениями чисел.

Пример: Найти произведение ПЧ №14(2,24) и ПЧ №22(3,55) ряда R40

i=i_2,24+i_3,55=14+22=36.

№36 предпочтительное число - 8.

Определение ряда по заданной последовательности чисел. Рассмотрим это свойство на примере определения ряда для конденсатора К50-35.

Для этого конденсатора следующие номинальные значения емкостей: 1; 2,2; 4,7; 10; 22; 47 мкФ. Требуется найти знаменатель ряда; указать обозначение ряда по ГОСТ.

а) По определению знаменателя ряда находим его значение как отношение соседних чисел ряда (как среднее арифметическое):

,

.

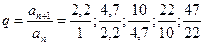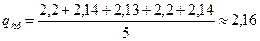б) Вычисленное число 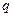близко расположено к 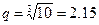. Это соответствует ряду по ГОСТу: Е3.

в) Проверяем, что заданные числа соответствуют числам представленным в таблице для найденного ряда.