Представление булевых функций

Любую булеву функцию можно представить в виде КНФ, ДНФ, СКНФ, СДНФ и полинома Жигалкина, доказательство данного утверждения выходит за рамки работы.

Простой конъюнкцией называется конъюнкция конечного набора переменных или их отрицаний, причём каждая переменная встречается не более одного раза.

Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций.

Например: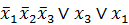

Совершенной дизъюнктивной нормальной формой (СДНФ) относительно некоторого заданного конечного набора переменных называется ДНФ, у которой в каждую конъюнкцию входят все переменные данного набора, причём в одном и том же порядке.

Например: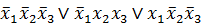

КНФ — это конъюнкция простых дизъюнкций.

СКНФ относительно некоторого заданного конечного набора переменных, называется такая КНФ, у которой в каждую дизъюнкцию входят все переменные данного набора, причём в одном и том же порядке.

Получить из КНФ эквивалентную ДНФ можно раскрыв скобки, верно и обратное.

Полином Жегалкина — это форма представления логической функции в виде полинома с коэффициентами вида 0 и 1, в котором в качестве произведения используется операция конъюнкции («И», AND), а в качестве сложения — сложение по модулю 2 (исключающее «ИЛИ», XOR).

Построение СДНФ

1. Построение по таблице истинности

1. Найти строки в ТИ, где f = 1.

2. Переписать все переменные в виде конъюнкции, причём, те переменные, где в строке значится 1 включить в конъюнкцию без изменений, а те, что равны 0 – инвертировать.

3. Составить дизъюнкцию из конъюнкций п.2.

2. Получение из ДНФ.

Если некоторое ДНФ не содержит какой-либо переменной (пусть x_k), то необходимо домножить это произведение на дизъюнкцию этой переменной и ее отрицания (т.е. на единицу, равную 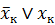) и применить дистрибутивный закон.

Построение СКНФ (если в таблице истинности функция чаще принимает значение1, чем 0 – имеет смысл использовать СКНФ, т. к. получится короче).

1. Построение по таблице истинности

1. Найти строки в ТИ, где f = 0.

2. Переписать все переменные в виде дизъюнкции, причём, те переменные, где в строке значится 0 включить в конъюнкцию без изменений, а те, что равны 1 – инвертировать.

3. Составить конъюнкцию из дизъюнкций п.2.

2. Получение из КНФ.

Если некоторое произведение КНФ не содержит какой-либо переменной (пусть x_k), то необходимо дизъюнктивно добавить в нее произведение этой переменной и ее отрицания (т.е. 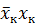) и применить дистрибутивный закон.

Примеры:

Пример получения СДНФ по таблице – рис. 3 и ниже п.3 – формула.

Переход КНФ в ДНФ:

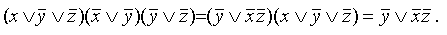
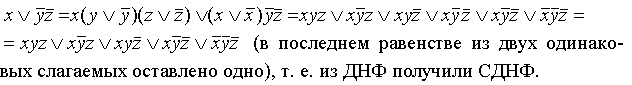Переход от ДНФ к СДНФ:

Получение полинома Жегалкина из ДНФ:

Учитывая 4 тождества:

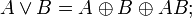
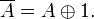
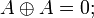
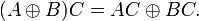
Получим:

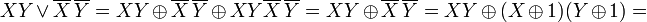
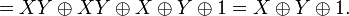
Карты Карно

Основным методом минимизации булевых функций, представленных в виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:

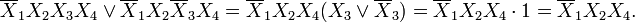
Если функция достаточно большая, то на это может уйти много времени. Ситуацию упрощает метод, названный картами Карно.

- карта Карно – это преобразованная таблица истинности (количество ячеек равно количеству значений функции)

- карту Карно удобно употребить при количестве переменных не более пяти.

-значения переменных выписываются в форме кода Грея, т. е. отличаются присутствием одной единицы (00 01 11 10 напр.). Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.о. вся Карта Карно сворачивается в фигуру тор.

- делим все переменные на 2 группы – одна для столбцов, другая – для строк, в примере ниже: первая группа - Х₁Х₂, вторая – Х_3.

- выписав в заголовки строк и столбцов значения переменных в форме кода Грея, заполняем таблицу соответствующими значениями функции.

- для получения ДНФ рассмотрим клетки с 1.

- объединяем смежные клетки, содержащие единицы, в области по 2ⁿ клеток (помним про то, что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток, содержащих нули.

- область должна быть как можно больше, а количество областей как можно меньше.

- области могут пересекаться.

- возможно несколько вариантов покрытия.

- берём каждую область и смотрим, какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных; если неменяющаяся переменная нулевая, проставляем над ней инверсию .

- выписанные конъюнкции объединяем дизъюнкцией.

- кстати, представив функцию графически, в виде куба, можно заметить, что склеиваемые вершины принадлежат одной грани.

Пример: карта Карно для рис. 3

Х1Х2 Х3

Рис. 9

Получим ДНФ: 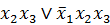(имеется 2 области, содержащие 1)

Запись функции в базисе (и-не либо или-не).

Запись логического выражения через базис подразумевает представление оного, используя только лишь базисную функцию (например, мы в радиомагазине купили исключительно двухвходовые элементы и-не, или технология подразумевает использование базиса).

Мы выше выяснили, что любую функцию можно записать в виде ДНФ и КНФ.

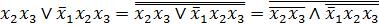
В примере выше, используя закон двойного отрицания и правило де Моргана, мы исключили дизъюнкцию из формулы. Теперь надо научится, использую функцию и-не выразить функцию не, если на оба входа схемы «И-НЕ» подать Х, то на выходе мы получим НЕ-Х, вот и всё, остаётся изобразить функцию в схемотехнических обозначениях.

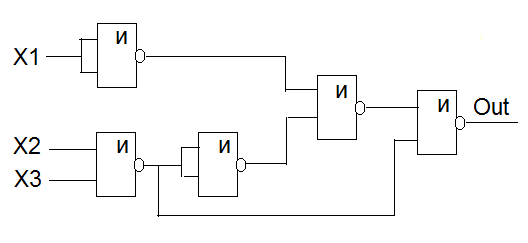
Рис. 10

Преобразование к базису ИЛИ-НЕ выполняется аналогично.

Вот мы и перешли от математики к схемотехнике.

Основные этапы синтеза комбинационных логических устройств:

1. Построение математической модели (системы логических уравнений) для устройства.

2. Минимализация уравнений в заданном базисе.

3. Построение логической схемы из базисных элементов.

4. Моделирование и испытание схемы.

5. Физическое воплощение модели.

При синтезе логического устройства могут накладываться дополнительные ограничения (напр. на максимальное количество, тип элементов).

Анализ проектируемого устройства выполняется на этапе построения и минимизации математической модели, на этапе моделирования и испытания (напр. в специальных компьютерных программах или с применением ПЛИС – аппаратно).

Может оказаться, что по условию проекта некоторые наборы значений аргументов запрещены (никогда не могут быть поданы на вход). Функция, заданная не на всех наборах аргументов называется не полностью заданной. Поскольку запрещённые аргументы в ходе эксплуатации никогда на входы устройства не поступят, постольку мы в ходе проектирования можем указать любые удобные значения функции в соответствующих строках таблицы истинности (напр. планируя составить СДНФ по таблице удобнее будет в запрещённых строках прописать нули, чтобы СДНФ получилась короче и тп.).

Особенности построения логических устройств.

Существуют логические элементы с разным количеством входов. Так, например, если у нас что-то и что-то и что-то, то надо применить либо трёхвходовое И, либо два двухвходовых (на второй элемент подаётся результат первого и третий аргумент). Но иногда число входов элемента избыточно (как в преобразовании И-НЕ в НЕ, см. выше). Тут возможны следующие варианты:

- оставить лишний вход висеть в воздухе откусив ножку схемы кусачками (помехонеустойчивый вариант).

- подключить неиспользуемый вход к используемому (как мы на схеме и сделали). В этом случае возрастание нагрузки увеличивает задержку распространения сигнала и снижение быстродействия элемента.

- самым удачным вариантом является подача на неиспользуемый вход 0 или 1, в зависимости от схемотехнического элемента ( 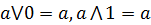).