Непрямые умозаключения логики высказываний
Непрямые умозаключения – это косвенные рассуждения. Они имеют довольно сложную структуру, потому что состоят не из суждений, а из умозаключений. В них одно умозаключение выводится из другого.
Этими формами выводов нередко пользуются в процессе аргументации, в частности, как средствами доказательств и опровержений. К непрямым умозаключениям относятся опровержение «путем сведения к абсурду», доказательство «от противного» и рассуждение по случаям.
Опровержение «путем сведения к абсурду» представляет собой непрямое умозаключение, в котором ложность некоторого суждения доказывается на основании того, что из данного суждения можно при помощи правильных умозаключений вывести противоречие.
Структура этого рассуждения такова. Сначала выдвигается некоторое предположение. Затем, используя правильные умозаключения, из него получают противоречие, на основании чего выдвинутое предположение признают ложным. Упрощенно форму вывода можно представить в следующем виде:
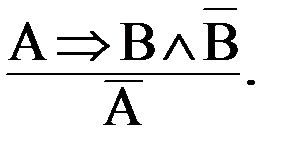
Основанием такого рассуждения является непротиворечивость как свойство нашего мышления. Противоречие используется как признак неправильности какого-либо умозаключения в нашем рассуждении или ложности какого-либо суждения.
Например, представим себе, что на некотором острове живут только рыцари и лжецы. Причем лжецы всегда лгут, а рыцари всегда говорят правду. Приехавший на остров человек встречает двух местных жителей и спрашивает, кто они такие. На что один из них отвечает: «По крайней мере, один из нас лжец». Необходимо узнать, кем является отвечавший.
Предположим, что он лжец. Обозначим суждение «Тот, кто ответил приезжему, – лжец» переменной А. Но тогда, по условию задачи, он сказал неправду и суждение «По крайней мере, один из нас лжец» ложно. Истинным же, согласно закону исключенного третьего, должно быть противоречащее высказывание. Следовательно, ни один из них не является лжецом и оба они – рыцари. Мы получили противоречие: отвечавший в одно и то же время рыцарь (В) и не рыцарь (`В). Значит, наше предположение неверно, и тот, кто отвечал, на самом деле является рыцарем, а не лжецом (`А).
Доказательство «от противного» близко к опровержению «путем сведения к абсурду». Однако, в отличие от «сведения к абсурду», которое направлено на опровержение некоторого суждения, доказательство «от противного» направлено на доказательство какого-либо суждения, хотя при этом оно также использует противоречие.
Структура данного умозаключения следующая. Допустим, нужно доказать истинность некоторого суждения. Временно предполагаем истинным суждение, противоречащее ему, т.е. его отрицание. Затем, как и в случае опровержения путем сведения к абсурду, при помощи правильных умозаключений выводим из этого предположения противоречие. И, если оно действительно выводится, значит сделанное предположение неверно, а следовательно, истинно само исходное суждение.
В виде схемы доказательство «от противного» можно представить так:
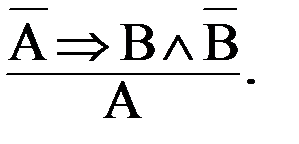
Это умозаключение использует закон двойного отрицания: отрицание отрицания некоторого суждения равносильно его утверждению (ùùАºА или ùùА®А).
В качестве примера можно использовать ту же самую ситуацию с рыцарями и лжецами, если изменить исходные предположения. Допустим, мы решили, что отвечавший – рыцарь, и хотим доказать это. Тогда временно допускаем, что он лжец, и выводим из этого противоречие. Тем самым доказываем истинность первоначального утверждения.
Рассуждение по случаям применяется тогда, когда необходимо сделать вывод из разделительного суждения (дизъюнкции). Поскольку на практике впрямую из дизъюнкции достаточно трудно делать выводы, рассуждение по случаям предлагает своего рода обходной маневр.
Принцип его заключается в следующем. Сначала смотрим, не следует ли интересующее нас суждение из всех альтернатив (случаев) дизъюнкции, и если следует, то его можно утверждать как следствие из всей дизъюнкции. Форма этого умозаключения:
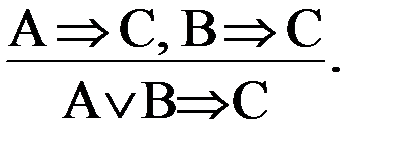
От условно-разделительных умозаключений (дилемм) это непрямое умозаключение отличается тем, что в его посылках фигурируют не суждения, а умозаключения (выводы).
Например, в свое время известный итальянский политический деятель и философ Николо Макиавелли (1469-1527) рассуждал следующим образом о кондотьерах[7]: «Кондотьеры по-разному владеют своим ремеслом: одни – превосходно, другие – посредственно. Первым нельзя довериться, потому что они сами будут добиваться власти… Вторым нельзя довериться, потому что они проиграют сражение».
В основе этого рассуждения лежит дизъюнктивная посылка «Кондотьеры по-разному владеют своим ремеслом: одни – превосходно, другие – посредственно». В логической форме это сложное суждение выглядит следующим образом: «Кондотьеры владеют своим ремеслом превосходно, или кондотьеры владеют своим ремеслом посредственно». Из этого суждения Макиавелли делает выводы, применяя непрямое умозаключение, а именно рассуждение по случаям. Он перебирает альтернативы (случаи) и показывает, что и в том, и в другом случае кондотьерам нельзя доверять. Рассмотрим схему этого рассуждения подробнее. В нем можно выделить следующие простые суждения:
s1 – «Кондотьеры владеют своим ремеслом превосходно»;
s2 – «Кондотьеры владеют своим ремеслом посредственно»;
r – «Кондотьерам нельзя довериться»;
р – «Кондотьеры сами будут добиваться власти»;
q – «Кондотьеры проиграют сражение».
s1 и s2 – это и есть альтернативы (случаи) дизъюнктивной посылки, лежащей в основе вывода. Посмотрим, каким образом делаются выводы из одного и другого случаев.
Первый случай: «Кондотьеры владеют своим ремеслом превосходно». Макиавелли говорит: «Если кондотьеры владеют своим ремеслом превосходно, то они сами будут добиваться власти»:
s1 ® р.
Далее: «Если они сами будут добиваться власти, то им нельзя довериться»:
р ® r.
Отсюда вытекает, что им нельзя довериться. Схема вывода будет такой:
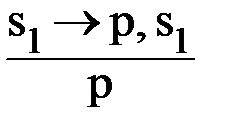 .
.
Следующий шаг:
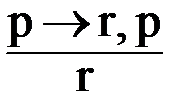 .
.
Второй случай: «Кондотьеры владеют своим ремеслом посредственно». Макиавелли утверждает, что если это так, то они проиграют сражение. Если же они проиграют сражение, то им опять же нельзя довериться. В целом, из этих посылок вытекает, что им нельзя довериться. Получается следующая схема вывода:
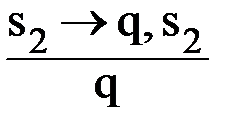 .
.
Следующий шаг:
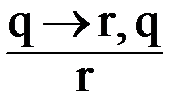 .
.
Таким образом, мы вывели r из s1 и s2. Это означает, что можно утверждать вывод r из s1 Ú s2, т.е. s1 Ú s2 Þ r.
В результате получилась схема рассуждения по случаям:

