Алгебраические операции над нечеткими множествами

Алгебраическое произведение А и В обозначается 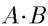и определяется так: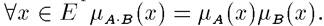

Алгебраическая сумма этих множеств обозначается 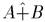и определяется так: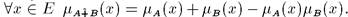

Для операций {•, +} выполняются свойства:

1)

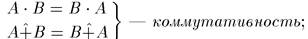
2).

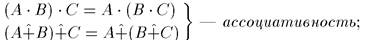
3)

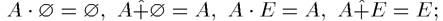
4)

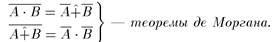
Не выполняются:

1)идемпотентность;

2) дистрибутивность;

3)

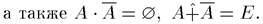
Замечание. При совместном использовании операций 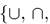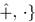выполняются свойства:

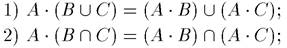
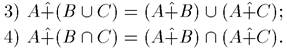
На основе операции алгебраического произведения определяется операция возведения в степень а нечеткого множества А, где a — положительное число. Частным случаем

возведения в степень являются:

1) CON (А) = А2 — операция концентрирования (уплотнения);

2) DIL (А) = А0'5 — операция растяжения, которые используются при работе с лингвистическими неопределенностями (рис. 1.4).

Умножение на число. Если а — положительное число, такое,

что 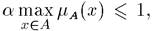, то нечеткое множество имеет функцию принадлежности:

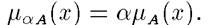
Декартово (прямое) произведение нечетких множеств.

Пусть 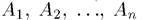— нечеткие подмножества универсальных

множеств 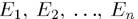соответственно. Декартово, или прямое

произведение 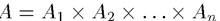является нечетким подмножеством множества 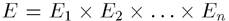с функцией принадлежности:

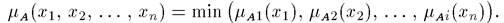
Нечеткая и лингвистическая переменные

Четкое множество 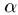-уровня (или уровня 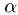). Множеством 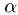-уровня нечеткого множества А универсального множества Е называется четкое подмножество 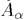универсального множества Е,

определяемое в ви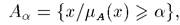де

где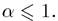

Декомпозиция

Любое нечеткое множество А можно представить в виде

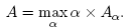
Нечеткая и лингвистическая переменные

Понятие нечеткой и лингвистической переменных используется при описании объектов и явлений с помощью нечетких множеств.

Нечеткая переменная характеризуется тройкой 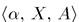, где 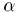- наименование переменной; X — универсальное множество (область определения 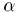); А — нечеткое множество на X, описывающее ограничения на значения нечеткой переменной .

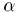Нечеткие числа — нечеткие переменные, определенные на числовой оси, т.е. нечеткое число определяется как нечеткое множество А на множестве действительных чисел R с функцией принадлежности 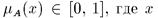действительное число, т.е.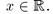

Операции над нечеткими числами. Расширенные бинарные арифметические операции (сложение, умножение и пр.) для нечетких чисел определяются через соответствующие операции для четких чисел с использованием принципа обобщения следующим образом.

Пусть Аи В — нечеткие числа, и 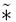- нечеткая операция, соответствующая произвольной алгебраической операции * над обычными числами. Тогда (используя здесь и в дальнейшем обозначения 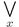вместо 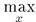и 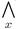вместо 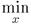) можно записать

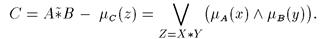
Отсюда:

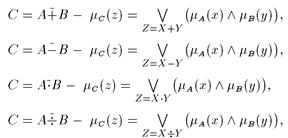
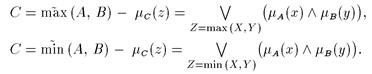
Вопрос2