Основные законы распределения
| № п/п | Вид распределения | Р(х) | К = Dэ/s. |
| 1. Трапецеидальные: | |||
| 1. равномерное | s = а/Ö 3 Р(х) хц=(х1+х2)/2 1/2а а а х1 хц х2 х | = 0, при х < xц - а, х> хц + а; = 1/2а при xц – а £ х £ хц + а | 0,73 |
| 2. Трапецеидальное | хц=(х1+х2)/2 Р(х) 1/(а+в) в в х1 хц х2 х 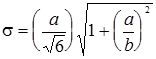 | = 0, при х < xц - а, х< хц + а; х- xц + а а2 - в2 а + в -х+ xц + а а2 - в2 | 1,73 1,83 1,94 2,00 2,02 |
| 3. Треугольное (Симпсона) | хц=(х1+х2)/2 Р(х) 1/а а а х1 хц х2 х s = а/Ö 6 | = 0, при х < xц - а, х< хц + а; 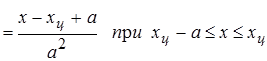 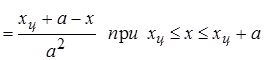 | 2,02 |
3. Экспоненциальные. Все распределения в общем виде описываются формулой: a - характеристика распр.-я. 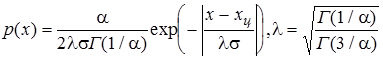 Г (х) – гамма функция. Г (х) – гамма функция. | |||
| 1. Лапласа | a = 1 Р(х) 0,5 -3 –2 –1 0 1 2 3 | 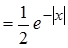 | 1,92 |
| 2. Нормальное распределение | a = 2 0,55 Р(х) -2 -1 0 1 2 | 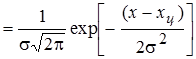 | 2,066 |
| 3. равномерное. | a = ¥ | 1,73 | |
        4. Уплощенные (равномерное + ехр.) 4. Уплощенные (равномерное + ехр.) | Показатель относительного содержания в композиции равномерной составляющей. Ср = sр/sэкс. Вес относительной дисперсии sэкс. 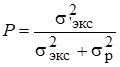 в суммарной дисперсии в суммарной дисперсии 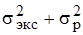 не превышает 10 % не превышает 10 % | ||
| 4. Двухмодальные распределения. | |||
    1. Дискретное двузначное 1. Дискретное двузначное | s = а а а | = 0,5d (х + а) + 0,5d(х – а); d(х) дельта-функция Дирака. | |
       2. арксинусоидальное 2. арксинусоидальное | а а | = 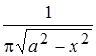 | 1,11 |
         3. Островершинные 3. Островершинные | -а а | Композиция дискретного двузначного и экспоненциального распределения. Показатель относительного содержания в композиции дискретной составляющей. Сд = sд/sэкс. Сд как правило находится в интервале [0,2]; чем это значение больше, тем глубже провал, а пр Сд=0 провал отсутствует. | 1,76 |
       4. Кругловершинные 4. Кругловершинные | -а а |
Равномерное распределение имеют погрешности: округления при расчетах, квантования и отсчета показаний стрелочных приборов. Складываясь между собой эти погрешности образуют трапецеидальные распределения.
В экспоненциальных распределениях константа aоднозначно определяет вид и параметры распределения. При a < 1 это распределение близко к распределению Коши. При a = 1 получаем распределение Лапласа, при a = 2 нормальное распределение Гаусса.
При a > 2 распределение близко к трапецеидальному распределению, а при больших значениях равномерному.
