Список используемых источников
Задание 1. Количество информации. Единицы измерения информации.
1.1. Туристическая фирма продает туры в различные города России. Купив тур в один из этих городов, мы получили 3 бита информации. Сколько туров продает туристическая фирма?
| Дано | Решение | |
| i = 3 бита | N = 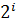 ; N = ; N = 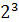 ; N = 8 ; N = 8 | |
| Найти N |
Ответ: фирма продает 8 туров
1.3. Сколько килобайтов составит сообщение из 384 символов 16-ти символьного алфавита?
| Дано | Решение | |
| N = 16 K = 384 | Найдем какое кол-во информации несет 1 знак алфавита: N = 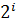 ; 16 = ; 16 = 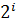 ; i = 4 бита ; i = 4 бита | |
| Найти Ic | Найдем сколько бит занимает сообщение, где Ic – кол-во информ. в сообщении, К – кол-во знаков: Ic = K * i; Ic = 384 * 4 = 1536 бит Переведем в килобайты: 1536 / 1024 = 1,5 килобайта |
Ответ: 1,5 килобайта
1.2. Репертуар драматического театра на следующий месяц составляет 25 спектаклей, причем 4 спектакля по пьесам Островского, 2 – по произведениям Гоголя, 3 – по пьесам Чехова, и остальные спектакли по другим писателям. Какое суммарное количество информации мы получим, посмотрев один спектакль по пьесе Островского, один спектакль по произведениям Гоголя, один спектакль по пьесам Чехова?
Решение:
При неравновероятностном подходе используем формулу Шеннона
P =  (где K — количество тех наблюдений, при которых рассматриваемое событие наступило, N — общее количество наблюдений):
(где K — количество тех наблюдений, при которых рассматриваемое событие наступило, N — общее количество наблюдений):
1) Общее количество событий равно: 25 – 4 + 2 + 3 = 16;
2) Вероятность просмотра спектакля Островского: 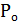 =
= 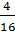 =
=  ;
;
Вероятность просмотра Гоголя: 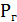 =
= 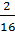 =
=  ;
;
Вероятность просмотра Чехова: 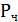 =
= 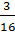 ;
;
3) Теперь найдем количество информации, используя формулу  =
= 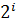 :
:
Кол-во информ. Островского: 1 /  =
= 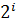 , i = 2 бита;
, i = 2 бита;
Кол-во информ. Гоголя: 1 /  =
= 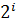 , i = 3 бита;
, i = 3 бита;
Кол-во информ. Чехова: 1 / 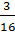 =
= 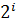 , i = 2 бита;
, i = 2 бита;
Найдем суммарное количество информации: 2 бита + 3 бита + 2 бита = 7 битов
Ответ: 7 битов
Задание 2. Представление чисел в позиционных системах счисления (СС). Перевод чисел из одной системы в другую систему счисления
2.1. Произведите перевод числа 117. 38 из десятичной СС в двоичную, восьмеричную и шестнадцатеричную СС.
Переведем 117, 38 в двоичную СС. Целая часть числа находится делением на основание новой:
| -116 | |||||||
| -58 | |||||||
| -28 | |||||||
| -14 | |||||||
| -6 | |||||||
| -2 | |||||||
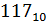 =
= 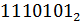
Дробная часть числа находится умножением на основание новой:
0,38 * 2 = 0,76 * 2 = 1,52 * 2 = 1,04
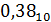 =
= 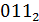
Сложим вместе целую и дробную части:
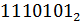 +
+ 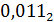 =
= 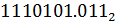
Переведем 117, 38 в восьмеричную СС. Целая часть числа находится делением на основание новой:
| -112 | |||
| -8 | |||
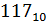 =
= 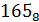
Дробная часть числа находится умножением на основание новой:
0,38 * 8 = 3,04
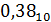 =
= 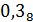
Сложим вместе целую и дробную части:
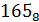 +
+ 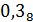 =
= 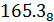
Переведем 117, 38 в шестнадцатеричную СС. Целая часть числа находится делением на основание новой:
| -112 | ||
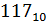 =
= 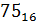
Дробная часть числа находится умножением на основание новой:
0,38 * 16 = 6,08
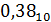 =
= 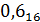
Сложим вместе целую и дробную части:
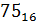 +
+ 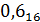 =
= 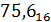
2.2. Полученное в пункте 2.1 двоичное число, перевести в десятичную, восьмеричную и шестнадцатеричную СС.
Переведем число 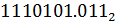 в десятичную СС:
в десятичную СС:
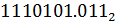 = 1∙
= 1∙ 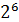 + 1∙25 + 1∙24 + 0∙23 + 1∙22 + 0∙21 + 1∙20 + 0∙2 -1+ 1∙2-2 + 1∙2-3=
+ 1∙25 + 1∙24 + 0∙23 + 1∙22 + 0∙21 + 1∙20 + 0∙2 -1+ 1∙2-2 + 1∙2-3=
= 64+32+16+0+4+0+1+0+0.25+0.125 = 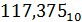
Переведем число 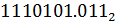 в восьмеричную СС:
в восьмеричную СС:
Для перевода двоичного числа в восьмеричное следует воспользоваться следующим алгоритмом:
- разделить целую часть числа на триады от младших разрядов к старшим (влево от запятой);
- разделить дробную часть на триады в обратном направлении (вправо от запятой);
- недостающие до триады позиции заполнить незначащими нулями;
- воспользоваться таблицей преобразованных триад.
| Двоичные триады | ||||||||
| Восьмеричные цифры |
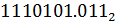 = 001 110 101, 011 =
= 001 110 101, 011 = 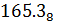
Переведем число 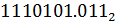 в шестнадцатеричную СС:
в шестнадцатеричную СС:
Для перевода двоичного числа в шестнадцатеричное воспользуемся тем же алгоритмом, что и при переводе в восьмеричную СС, только разобьем число на тетрады.
| Двоичные тетрады | ||||||||||
| шестнадцатеричные цифры | ||||||||||
| А | B | C | D | E | F | |||||
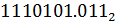 = 0111 0101, 0110 =
= 0111 0101, 0110 = 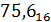
2.3 Полученное в пункте 2.1 восьмеричное число, перевести в двоичную, десятичную и шестнадцатеричную СС.
Для перевода числа из восьмеричной системы счисления в двоичную необходимо каждую цифру этого числа представить триадой:
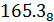 – 1 = 001, 6 = 110, 5 = 101, 0.3 = 011
– 1 = 001, 6 = 110, 5 = 101, 0.3 = 011
Примечание: незначащие нули слева и справа не записываются.
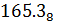 =
= 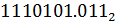
Переведем число 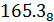 в десятичную СС:
в десятичную СС:
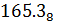 = 1∙
= 1∙ 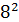 +6∙
+6∙ 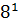 +5∙
+5∙ 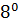 +3∙
+3∙ 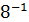 = 64+48+5+0,375 =
= 64+48+5+0,375 = 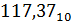
Переведем число 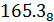 в шестнадцатеричную СС:
в шестнадцатеричную СС:
Для этого переведём восьмеричное число в двоичное, а затем уже в шестнадцатеричное. В двоичное мы уже переводили ранее, поэтому просто полученный результат разобьем на тетрады:
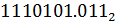 – 0111 = 7, 0101 = 5, 0.0110 = 6
– 0111 = 7, 0101 = 5, 0.0110 = 6
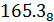 =
= 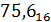
2.4. Полученное в пункте 2.1 шестнадцатеричное число, перевести в двоичную, восьмеричную и десятичную СС.
Для перевода числа из шестнадцатеричной СС в двоичную необходимо каждую цифру этого числа записать тетрадой:
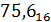 – 7 = 0111, 0101 – 5, 0.6 = 0110
– 7 = 0111, 0101 – 5, 0.6 = 0110
Примечание: незначащие нули слева и справа не записываются.
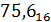 = 1110101,011
= 1110101,011
Переведем число 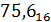 в восьмеричную СС:
в восьмеричную СС:
Для этого переведём шестнадцатеричное число в двоичное, а затем уже в восьмеричное. В двоичное мы уже переводили ранее, поэтому просто полученный результат разобьем на триады.
Примечание: Крайние неполные ряды дополняются нулями.
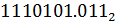 – 001 110 010, 011
– 001 110 010, 011
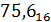 =
= 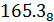
Переведем число 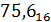 в десятичную СС:
в десятичную СС:
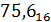 = 7∙
= 7∙ 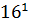 +5∙
+5∙ 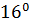 +6∙
+6∙ 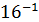 = 112+5+0.375 =
= 112+5+0.375 = 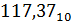
Задание 3. Двоичная арифметика
Числа 35 и 7 переведите в двоичную систему счисления и произведите над ними следующие арифметические операции:
( B )2 + ( C )2, ( B )2 – ( C )2, ( B )2 * ( C )2, ( B )2 / ( C )2.
| -34 | ||||||
| -16 | ||||||
| -8 | ||||||
| -4 | ||||||
| -2 | ||||||
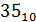 =
= 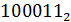
| -6 | |||
| -2 | |||
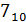 =
= 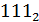
| ( B )2 + ( C )2 | ( B )2 – ( C )2 | ( B )2 * ( C )2, | ( B )2 / ( C )2. |
| 100011 / 111 | |||
| + 111 | - 111 | * 111 | - 111 101 |
| + 100011 | |||
| + 100011 | |||
| + 100011 | |||
Проверка:
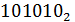 = 1∙25 + 0∙24 + 1∙23 + 0∙22 + 1∙21 + 0 = 32+0+8+0+2+0 = 4210
= 1∙25 + 0∙24 + 1∙23 + 0∙22 + 1∙21 + 0 = 32+0+8+0+2+0 = 4210
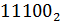 = 1∙24+1∙23+1∙22+0∙21+0∙20 = 16+8+4+0+0 = 2810
= 1∙24+1∙23+1∙22+0∙21+0∙20 = 16+8+4+0+0 = 2810
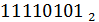 =1∙27+1∙26+1∙25+1∙24+0∙23+1∙22+0∙21+1∙20=128+64+32+16+0+4+0++1 = 24510
=1∙27+1∙26+1∙25+1∙24+0∙23+1∙22+0∙21+1∙20=128+64+32+16+0+4+0++1 = 24510
Задание 4. Представление чисел в машинных кодах. Выполнение арифметических операций над числами, представленными в машинных кодах
Числа 311, -311, 89 и -89 представьте в прямом, обратном и дополнительном кодах. Размер разрядной сетки 2байта.
Произведите сложение чисел в машинных кодах по схеме:
D + E D + ( -E ) ( -D ) + E ( -D ) + ( -E ).
Прямой код двоичного числа совпадает с записью самого числа:
311 (ПК) – 0|000 0001 0011 0111
-311 (ПК) – 1|000 0001 0011 0111
89 (ПК) – 0|000 0000 0101 1001
-89 (ПК) – 1|000 0000 0101 1001
Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные, а в знаковый разряд заносится единица.
311 (ОК) – 0|000 0001 0011 0111
-311 (ОК) – 1|111 1110 1100 1000
89 (OК) – 0|000 0000 0101 1001
-89 (OК) – 1|111 1111 1010 0110
Дополнительный код положительного числа совпадает с прямым кодом. Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы.
-311 (ОК) – 1|111 1110 1100 1000
+1
-311(ДК) – 1|111 1110 1100 1001
-89 (OК) – 1|111 1111 1010 0110
+1
-89 (ДК) – 1|111 1111 1010 0111
| 311 + 89 = 400 | 311 + (-89) = 222 |
| 0|000 0001 0011 0111 + 0|000 0000 0101 1001 | 0|000 0001 0011 0111 + 1|111 1111 1010 0111 |
| 0|000 0001 1001 0000 | 0|000 0000 1101 1110 |
| (-311) + 89 = -222 | (-311) + (-89) = - 400 |
| 1|111 1110 1100 1001 + 0|000 0000 0101 1001 | 1|111 1110 1100 1001 + 1|111 1111 1010 0111 |
| 1|111 1111 0010 0010 | 1|111 1110 0111 0000 |
Задание 5. Представление символьной информации в памяти ЭВМ
Используя таблицу ASCII, закодируйте число, месяц Вашего рождения.
9 января Finland
| пробел | |
| я | |
| н | |
| в | |
| а | |
| р | |
| я | |
| пробел | |
| F | |
| i | |
| n | |
| l | |
| a | |
| n | |
| d |
Задание 6. Выполнение логических операций. Построение таблиц истинности
Постройте таблицу истинности логической функции ( A V B ) & ( A ® Ø B ) и укажите какой является эта функция (тавтологией, противоречием или выполнимой).
Кол-во высказываний – 2; n = 2; 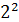 = 4 + 1 = 5
= 4 + 1 = 5
Кол-во столбцов – переменные + операторы – 2 + 4 = 6
| А | В | A V B | Ø B | A ® Ø B | ( A V B ) & ( A ®Ø B) |
Функция является выполнимой, т.к. хотя бы при одном наборе выполняется истина.
Задание 7. Преобразование логических выражений с использованием законов алгебры логики
Преобразуйте логическое выражение ( A V B ) & ( A ® Ø B ) используя законы алгебры логики.
( A V B ) & ( A ® Ø B )
( А V B ) & (Ø A V Ø B)
A Ø A V A Ø B V B Ø A V B Ø B
A Ø B V B Ø A
Задание 8. Построение логических схем
8.1. Для логического выражения ( A V B ) & ( A ® Ø B ) постройте логическую схему из простейших логических элементов.
Упростим до ( А V B ) & (Ø A V Ø B)
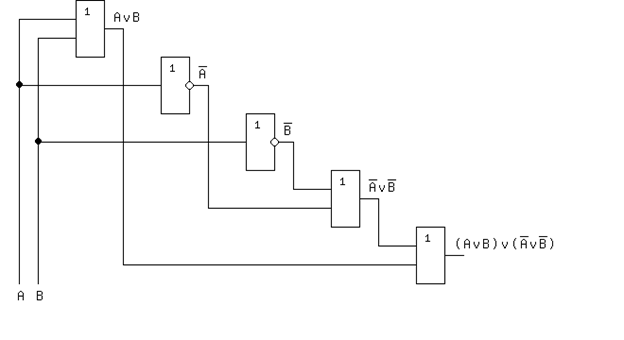
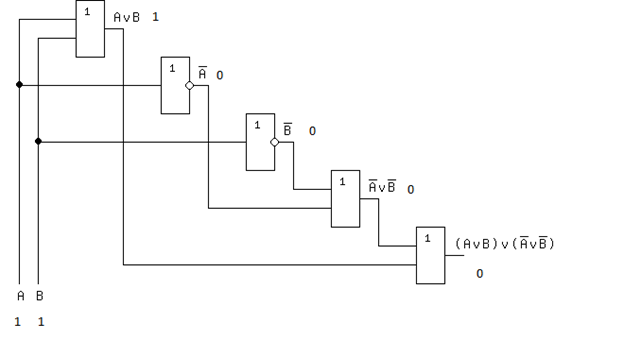
8.2. На входы схемы, построенной в п.8.1, подаются сигналы: X=1 и Y=1. Указать на схеме, какие сигналы будут получены на промежуточных узлах построенной схемы и на выходе схемы.
Список используемых источников
1. О. Нейгебавуэр "Точные науки в древности" // М.: пер. с англ., изд. "Наука", -1968. -224 с.
2. И.Я. Депман "История арифметики" // М.: изд. "Просвящение", -1965. -415 с.
3. Е.А. Башков "Аппаратное и программное обеспечение зарубежных ЭВМ" // Учеб. пособие.- К.: Выща школа. -1990. -207 с.
4. С.Д. Погорелый, Т.Ф. Слободянюк "Программное обеспечение микропроцессорных систем: Справочник" // 2-е изд., перераб. и доп. - К.: Тэхника. -1989. -301 с.
5. Р. Токхайм "Микропроцессоры: Курс и упражнения" // пер. с англ., под ред. В.Н. Грасевича. М.: Энергоатомиздат. -1988. -336 с.
6. В. Юров "Assembler" // СПб: Издательство "Питер". -2000. -624 с.
7. У. Девис "Операционные системы. Функциональный подход" // Пер. с англ., М.: изд. "Мир". -1980. -436 с.
8. Д.В. Иртегов "Введение в операционные системы" // СПб.: БХВ-Петербург, -2002. -624 с.
9. С.В. Зубков "Assembler для DOS, Windows и Unix" // М.: ДМК Пресс. -2000. -608 с.
10. Э. Таненбаум "Архитектура компьютера" // пер. с анг., под ред. А.В. Гордеева. СПб.: Питер. -2002. -704 с.
11. З.Л. Рабинович, В.А. Раманаускас "Типовые операции в вычислительных машинах" // К.: Техніка, -1980. -264 с.
12. Б. Бериан "Программирование на языке ассемблера системы IBM/370. Упрощенный подход" // М.: "Мир", -1980. -640 с.
