Алгоритм количественного вариационного анализа.
I. Вычислить выборочную среднюю 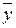 по формуле:
по формуле:
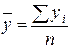 (1)
(1)
где n – объем выборки, то есть количество обследованных объектов. В примере n = 4 – четыре делянки со стевией по 100 м2.
Вычисления по формуле (1) приведены ниже в первом столбце.
| уi ц/га | ( 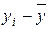 ), ц/га ), ц/га | ( 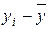 )2, ( ц/га)2 )2, ( ц/га)2 |
| (исходные данные) | (центральные отклонения) | (квадраты центральных отклонений) |
| 70 – 68,75 = 1,25 | 1,252 = 1,5625 | |
| 68 – 68,75 = – 0,75 | – 0,752 = 0,5625 | |
| 72 – 68,75 = 3,25 | 3,252 = 10,5625 | |
| 65 – 68,75 = – 3,75 | – 3,752 = 14,0625 | |
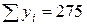 ц ц | ||
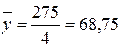 ц/га ц/га | 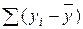 = –4,5 + 4,5 = 0 = –4,5 + 4,5 = 0 | 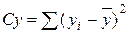 =26,75 ц2 =26,75 ц2 |
| Это закон! |
Сумма отклонений исходных данных от выборочной средней всегда равна нулю (см. второй столбец вычислений), так как выборочная средняя является центром изменчивости любого признака. Вот почему разности ( 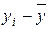 ) называютсяцентральными отклонениями.
) называютсяцентральными отклонениями.
Таким образом, сумма центральных отклонений всегда равна нулю. Это их свойство не позволяет вычислить среднее центральное отклонение, которое является обобщенной мерой изменчивости и называется упомянутым выше стандартным отклонением любого признака. Приходится вычислять его косвенно – через квадраты центральных отклонений.
II. Вычислить сумму квадратов центральных отклонений, выражающую общее варьирование исследуемого признака Су
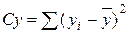 (2)
(2)
Прямой способ определения общего варьирования показан выше в третьем столбце вычислений. Он четко раскрывает математическую природу общего варьирования, наглядно показывая, что это сумма квадратов центральных отклонений. Но он требует громоздких вычислений, поэтому в практике исследований его почти всегда заменяют более простыми косвенными вычислениями по формулам (2'):
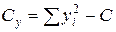 ,
, 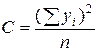 (2')
(2')
где С – поправка
В нашем примере:
С = 2752 : 4 = 75625 : 4 = 18906,25
Су = 702 + 682 + 722 + 652 – С = 18933 – 18906,25 = 26,75 ц2 –
та же величина, что и при прямом способе вычислений.
|
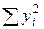 на обычном микрокалькуляторе воспользуйтесь следующей программой:
на обычном микрокалькуляторе воспользуйтесь следующей программой:
|
|
|
2. Наберите первое число и нажми и
3. Повторите второе действие с каждым следующим числом, включая последнее.
|
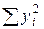
III. Вычислить дисперсию s2 – средний квадрат центральных отклонений.
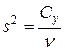 (3)
(3)
где 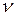 – число степеней свободы варьирования центральных отклонений. Оно показывает сколько центральных отклонений не зависят друг от друга. Одно из них математически лишено свободы иметь произвольную величину, так как оно должно равняться сумме остальных центральных отклонений, взятой с противоположным знаком. Иначе общая их сумма не была бы равна нулю, вопреки подчеркнутому выше закону. Значит,
– число степеней свободы варьирования центральных отклонений. Оно показывает сколько центральных отклонений не зависят друг от друга. Одно из них математически лишено свободы иметь произвольную величину, так как оно должно равняться сумме остальных центральных отклонений, взятой с противоположным знаком. Иначе общая их сумма не была бы равна нулю, вопреки подчеркнутому выше закону. Значит,
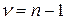
Следовательно, дисперсия показывает, сколько варьирования приходится на одну степень свободы. В нашем примере:
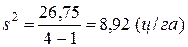 2
2
Только теперь появилась возможность косвенно, через средний квадрат, центральных отклонений, вычислить обобщенную меру изменчивости исследуемого признака – его стандартное отклонение.
IV. Вычислить стандартное отклонение s по формуле (4):
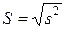 (4)
(4)
Следовательно, стандартнее отклонение этосреднее центральное отклонение признака, вычисленное косвенно - через квадраты центральных отклонений. В нашем примере:
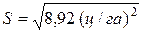 = 2,99 ц/га
= 2,99 ц/га
Теперь переходим к вычислению критериев для будущих выводов об одной ГСО, так как у выборочной средней и стандартного отклонения одинаковые единицы измерения, а значит,их можно объединять в соответствующих формулах.
V. Вычислить коэффициент вариации как критерий для вывода о степени изменчивости исследуемого признака:
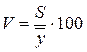 (5)
(5)
Коэффициент вариации исследуемого признака это его стандартное отклонение, выраженное в процентах к выборочной средней.
Принята следующая градация изменчивости объектов по количественным признакам:
| V, % | Изменчивость | |
| < 10 | Слабая | |
| 10 – 20 | Средняя | |
| 20,1 – 40 | Сильная | |
| > 40 | Очень сильная |
В нашем примере
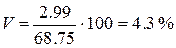
Значит, изменчивость урожайности стевии по территории предгорно-степной зоны Крыма, будет слабая, что является положительным свойством культуры. Правда, формулирование выводов не входит в задачи вариационного анализа.
VI. Вычислить 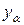 – размах варьирования исследуемого признака в ГСО
– размах варьирования исследуемого признака в ГСО
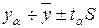 (6)
(6)
где 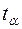 - критерий Стьюдента. Это множитель для перехода от неприемлемого для выводов 32%-ного уровня значимости, на котором вычисляется s по его формуле, к приемлемому уровню значимости, например, 5%-ному.
- критерий Стьюдента. Это множитель для перехода от неприемлемого для выводов 32%-ного уровня значимости, на котором вычисляется s по его формуле, к приемлемому уровню значимости, например, 5%-ному.
Критерий Стьюдента находят в приложении 1 настоящего методического пособия или у Б.А.Доспехова (на стр. 317), по такой схеме: по горизонтали выбирают графу с приемлемым уровнем значимости, по вертикали берут строку со своим числом степеней свободы. На их пересечении читают величину критерия Стьюдента.
В нашем примере при 5%-ном уровне значимости и 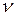 =3,
=3, 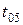 = 3,182
= 3,182
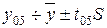
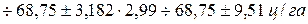
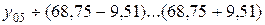 ц/га
ц/га
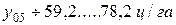
Это критерий для предсказания наименьшей и наибольшей урожайности стевии в Предгорно-степной зоне Крыма.
VII. Вычислить ошибку выборочной средней 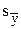 :
:
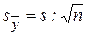 (7)
(7)
В нашем примере
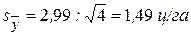
VIII. Вычислить доверительный интервал для генеральной средней 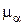 как критерий для вывода о наиболее вероятной средней величине признака в генеральной совокупности объектов:
как критерий для вывода о наиболее вероятной средней величине признака в генеральной совокупности объектов:
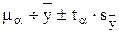 (8)
(8)
В нашем примере на 5%-иом уровне значимости имеем:
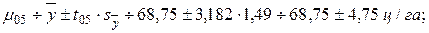
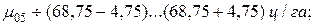
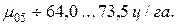
На этом вариационный анализ результатов монографического наблюдения завершен. По вычисленным критериям будут сделаны выводы об одной генеральной совокупности объектов (см. раздел 2). Но это уже задача не математического анализа, а логического и диалектического методов.
Раздел 2
