Метод последовательного исключения переменных с помощью законов и тождества алгебры-логики
Этот метод является наиболее простым. При этом, для минимизации используют чаще всего правила склеивания и поглощения.
(1)
Минимизация ПФ с большим числом переменных этим методом является задачей сложной, т.к. не всегда можно получить минимальную форму. Возможно получение тупиковой формы, т.е. такой, которая больше не упрощается, но не является минимальной.
Построим логическую функцию в Базисе1.
(на листике)
Построим эту функцию в Базисе 4.
(на листике)
Построим в Базисе 5 (ИЛИ-НЕ)
(на листике)
Минимизация логических функций методом Карно-Вече
Карта Карно-Вечай для двух переменных
| X1 | X1 | |
| X2 | ||
| X2 |
Для трёх
| X2X3 | X2X3 | X2X3 | X2X3 | |
| X1 | ||||
| X1 |
Для четырёх
| X3X4 | X3X4 | X3X4 | X3X4 | |
| X1X2 | ||||
| X1X2 | ||||
| X1X2 | ||||
| X1X2 |
Этот метод удобен для минимизации пФ содержащих обычно не более 4 х переменных. Диаграмма вече имеет вид прямоугольника разбитого на 2n клеток где N – число аргументов пФ каждой клетке диограммы ставится в соответствие определённая конюнкция, причём конюнкции в соседних клетках ( в строке или в столбце) должны отличаться не более чем значением одной переменной. Кроме того соседними на диограмме являются так же крайние ( левая и правая) конюнкци в одной строке и ( нижняя и верхняя) конюнкции в одном столбце в результате любые 2 соседние в строке или столбце конюнкции склеиваются по соответсвующей переменной. работа с (сднф)
Для минимизации пФ приводится к сднф после чего заполняется диограмы Вейча для Nпеременных при этом в соответствующую клетку диограммы вносится единица если пФ на данном наборе аргументов равна 1 ,остальные клетки остаются пустыми. В заполненной диаграмме обводят прямоугольными контурами клетки с 1 по следующим правилам :
1. Внутри контура должны быт клетки только с 1
2. количество клеток с 1 в контуре равно 2n где N =0,1,2,3… то есть равно 1,2,4,8…..
3.единицы а крайних клетках одного столбца или одной строки могут включаться в 1 контур
4. каждый контур должен включать как можно большее число клеток с 1 а общее число контуров должно быть кА моно меньше
После чего записывают минимальную Днф пФ в виде дизъюнкции простых импликант описыващих эти контуры в такие импликанты включаются те переменные которые во всех клетках контура имеют или только прямое или только инверстное значение.
Пример
Минимизировать пФ
F1=X1 X2+X1X2+X1X2 (2 переменные ранг равен 2м знаит совершенная форма)
| X1 | X1 | |
| X2 | ||
| X2 |
Fнднф =X1+X2
Пример 2
F=X1X2+X1X2X3+X1X2X3+X1X2X3 не совершенна
F=X1*X2*1+X1X2X3+X1X2X3+X1X2X3
F=X1*X2(X3+X3)+ X1X2X3+X1X2X3+X1X2X3
F=X1X2X3+X1X2X3 +X1X2X3+X1X2X3+X1X2X3
| X2X3 | X2X3 | X2X3 | X2X3 | |
| X1 | ||||
| X1 |
Fнднф=X1X3+X2X3+X2X3
Пример 3
F3=X1X2X3X4+X1X2X3X3+X1X2X3X4+X1X2X3X4+X1X2X3X4+X1X2X3X4+
X1X2X3X4+X1X2X3X4
| X3X4 | X3X4 | X3X4 | X3X4 | |
| X1X2 | ||||
| X1X2 | ||||
| X1X2 | ||||
| X1X2 |
F=X2X4+X2X3+X1X3X4+X1X2X3X4
Дз
F=abc +abc+abc+abc+abc
F=ac v bc v ac
| bc | bc | bc | bc | |
| a | ||||
| a |
F= X1X2X3X4+X1X2X3X4+X1X2X3X4+X1X2X3X4+X1X2X3X4+X1X2X3X4+X1X2X3X4+X1X2X3X4+X1X2X3X4
| X3X4 | X3X4 | X3X4 | X3X4 | |
| X1X2 | ||||
| X1X2 | ||||
| X1X2 | ||||
| X1X2 |
F=X1X2X3X4 vX2X3vX2X3
Понятие о цифровом автомате.
В эвм при образовании информации выполняется логическими схемами которые подразделяются на 2 класса :
1 комбинационные схемы или автоматы без памяти
2 последовательностные схемы или автомвты с памятью
Комбинационная схемы – схема в которой результат преобразования(выходняе сигналы ) зависит только от комбинации синалов поданных на её входы в анный момент времени.
Дз окр
Окр:
1Вычислительная система (ВС)– совокупность взаимосвязанных и взаимодействующих вычислителей (процессоров) и вычислительных машин периферийного оборудования (мышка, сканер, принтер и тд.) и программного обеспечения, предназначенного для подготовки и решения задач пользователей.
2Электронная вычислительная машина (ЭВМ)– комплекс технических средств, где основные и функциональные элементы (логические, запоминающие, индикационные и др.) выполнены на электронных элементах, предназначенный для автоматической обработки информации в процессе решения вычислительных и информационных задач.
3Математическая теория информации (американский ученый Клод Шеннон): информативность сообщения характеризуется содержащейся в нем полезной информацией – той частью сообщения, которая снимает полностью или уменьшает неопределенность какой-либо ситуации, т. е. информация – это уменьшение неопределенности наших знаний. Такой подход к информации позволяет ее количественно измерять.
4 Позиционная СС (ПСС) – это система, в которой значение цифры зависит от её положения в ряду цифр, изображающих число, т.е. веса каждого разряда. Основанием ПСС (p) называют максимальное количество различных цифр, используемых для записи чисел данной ПСС. Например, в десятичной ПСС p=10 – цифры от 0 до 9. 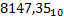 (8 – это
(8 – это 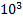 , 1 –это
, 1 –это 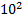 , 4 это 10, 7 это
, 4 это 10, 7 это 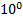 , 3 это
, 3 это 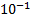 , 5 это
, 5 это 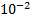 ). Т.е. для перевода в двоичную систему:
). Т.е. для перевода в двоичную систему:
8* 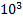 +1*
+1* 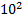 +4*10+7*
+4*10+7* 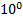 +3*
+3* 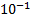 +5*
+5* 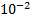
При переводе в десятичную из двоичной системы:
1011,01 = 1* 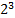 +0*
+0* 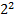 +1*
+1* 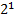 +1*
+1* 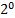 +0*
+0* 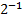 +1*
+1* 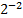 = 8+2+1+0,25 = 11,25
= 8+2+1+0,25 = 11,25
5Высказывание – это законченное предложение, которое может иметь два значения истинности: либо быть истинным (A истинно А=1), либо быть ложным (В ложное В=0).
Высказывания могут быть простыми и сложными: первые не зависят от других высказываний, а вторые образуются из двух и более простых высказываний.
Простые высказывания называют логическими переменными, а сложные – логическими функциями этих переменных (переключательными функциями – ПФ
6 Функционально-полной системой или базисом ПФ называют систему переключательных функций Ф‑1, Ф2, Фn, с помощью которой может быть представлена любая функция алгебры-логики.
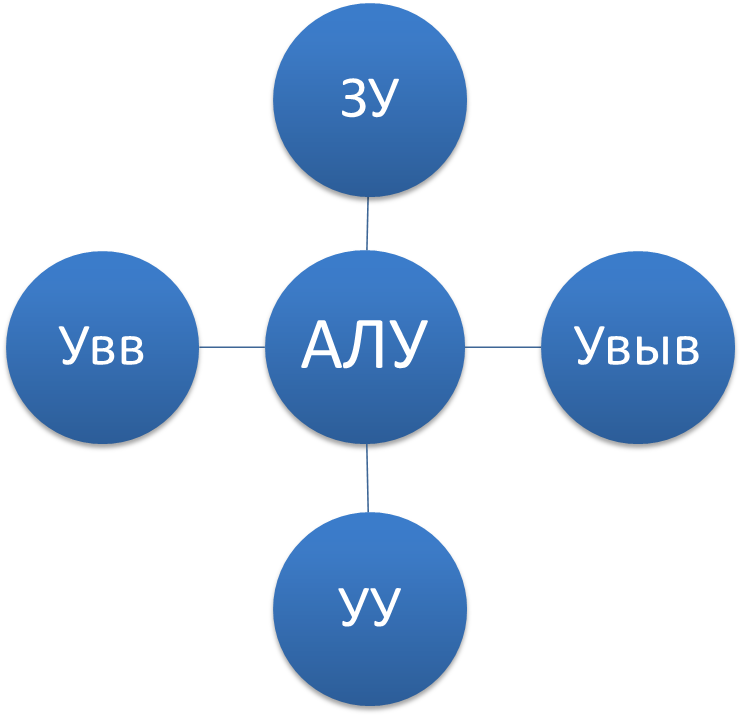
71) Структура ЭВМ
Структура ЭВМ представляет собой абстрактную модель, которая устанавливает состав, порядок и принципы взаимодействия основных функциональных частей ЭВМ без учета их реализации.
(стрелка)–коды данных и команд
(пункт стрелка)-управляющие сигналы
ЭВМ могут отличаться друг от друга конструктивным исполнением, быстродействием, точностью, но все они содержат 5 функциональных устройств:
· АЛУ – арифметико-логическое устройство
· УУ – устройство управления
· ЗУ – запоминающее устройство
· Увв – устройство ввода информации
· Увыв – устройство вывода информации
