Программирование ветвлений с составными условиями

Составное – условие одновременной проверки нескольких операций отношения (логических величин).

В математике запись составных условий осуществляется символами:

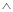– логическое умножение (И);

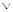– логическое сложение (ИЛИ);

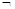– отрицание (НЕ).

Например, условием нахождения точки с координатами x, y в 1-м квадранте будет: x>0 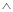y>0, а условие нахождения точки x вне отрезка (a,b) имеет вид: x<a 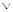x>b.

Символ «отрицание» позволяет расширить возможности формулировки логических условий.

Так, запись 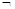a=b (не а равно b) позволяет сравнить операнды а и b как логические величины ИСТИНА или ЛОЖЬ. Если а и b есть ИСТИНА, то результат вычисления логического выражения есть ЛОЖЬ, т.к. левая часть (НЕ ИСТИНА) не эквивалентна правой (ИСТИНА).

Если один из операндов есть ЛОЖЬ, а другой – ИСТИНА, то результат вычисления выражения ( 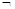a=b) есть ИСТИНА, т.к. левая часть становится эквивалентной правой.

Дополнительно символ НЕ существенно упрощает запись взаимоисключающих условий. Так условие расположения точки в конкретном квадранте плоскости, а тем более в пространстве, определяет очень громоздкое подробное перечисление остальных вариантов (см. начало главы). Использование символа НЕ делает взаимоисключающее условие максимально компактным, что подтверждает математическая модель нижеизложенной задачи.

Рассмотрим программирование разветвляющихся вычислительных процессов с проверкой составных условий на задаче (4.2) о положении точки.

Постановка задачи

Определить по заданным координатам (X, Y) положение точки на плоскости – первый квадрант или любой из остальных (второй, третий, четвёртый). Начало координат из рассмотрения исключить.

Формирование математической модели

Исходные данные

X=_ _ , _ _

Y=_ _ , _ _

Расчётные зависимости

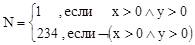
Выбор метода решения

Анализ полученного математического описания позволяет сделать выводы:

· проверяемые условия относятся к составным, т.к. содержат логическую операцию 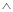над двумя логическими операндами (результатами операций отношения);

· вычисление номера квадранта может осуществляться по одной из двух ветвей:

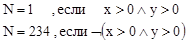
· номер каждой ветви задаётся в ней соответствующим равенством (N=1 – для первой и N=234 – для второй);

· условия

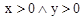и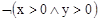

являются взаимоисключающими по записи, т.е. выполнение одного приводит к невыполнению другого и наоборот. Таким образом, проверять можно только одно условие, например

;

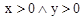· результат проверки выбранного условия до проведения вычислений неясен, поэтому необходимо предусмотреть возможность расчёта по любой из ветвей.

Следовательно, в качестве метода решения можно использовать простой ветвящийся процесс с проверкой одного составного условия x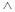>0 y>0.