Типовые фаззификаторы и дефаззификаторы

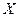Фаззификатор осуществляет отображение четкой точки (где - универсальное множество) в нечеткое множество в 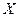. Существуют два возможных варианта такого отображения:

Синглетон - фаззификатор (singleton fuzzifier); в этом случае нечеткое множество определяется как:

;

Несинглетон - фаззификатор (nonsingleton fuzzifier); в этом случае и значение 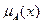убывает. Например,

,

где - параметр, характеризующий форму .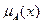

Примечание. Во многих приложениях, включая управление динамическими объектами, используется синглетон - фаззификатор, несинглетон - фаззификатор может быть полезен там, где данные подвержены искажению шумом.

Целью процесса дефаззификации является извлечение четкого выходного значения из результата нечеткого вывода , .

Таким образом, дефаззификатор осуществляет отображение нечеткого множества в в четкую точку .Существуют несколько вариантов такого отображения, например, такие:

· максимум-дефаззификатор (maximum defuzzifier) определяется как

(взять аргумент супремума функции);

· дефаззификатор «по центру тяжести» (center of gravity defuzzifier):

для непрерывного случая;

и

для дискретного случая,

где - результата нечеткого вывода после применения всех правил.

· дефаззификатор «средний максимум» (center average defuzzifier):

,

где - выходное нечеткое множество после применения нечеткого правила l, - значение центра (максимума) нечеткого множества , M – число нечетких правил.

Нечеткие системы как универсальные аппроксиматоры

Методология нечеткого моделирования основана на важнейших теоремах (необходимые и достаточные условия), согласно которым нечеткие системы обладают свойствами универсальных аппроксиматоров (universal approximators ).

Теорема о необходимых условиях (Wang L.-X., Kosko B.): Для любой действительной непрерывной функции 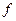на компактном множестве и произвольной существует нечеткая логическая система 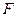(с нечеткой импликацией в виде нечеткой конъюнкции (умножения), с синглетон-фаззификатором, дефаззификатором «по центру тяжести» и Гауссовскими функциями принадлежности) такая, что

.

Эти теоремы были доказаны Wang L.-X. [7] и Kosko B.

Теорема о достаточных условиях: Нечеткая логическая система может аппроксимировать любую действительную непрерывную функцию.

Эта теорема была доказана Buckley J.J.

Эти две теоремы объясняют, почему нечеткие системы так привлекательны в инженерных приложениях теории управления: нечеткие контроллеры могут рассматриваться как универсальные аппроксиматоры систем с неизвестной динамикой и структурой.

Типовые Нечеткие Модели

Рассмотрим три наиболее популярные нечеткие модели, используемые в управлении.

Нечеткая Модель Мамдани

В нечеткой модели Мамдани (Mamdani fuzzy model) используются следующие нечеткие правила (общий вид):

ЕСЛИ И И … И ТО ,

где - входные переменные нечеткой модели, 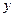- выходное значение; - индекс нечеткого правила, (число нечетких правил); - множество функций принадлежности, описывающих входную переменную ; - множество функций принадлежности, описывающих входную переменную 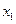; … - множество функций принадлежности, описывающих входную переменную ; - множество функций принадлежности, описывающих выходную переменную .

В общем виде, четкое выходное значение в нечеткой модели Мамдани (с нечеткой конъюнкцией в виде умножения, синглетон - фаззификатором и дефаззификатором «средний максимум») вычисляется по следующей формуле:

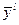- точка максимального значения (центра) .

На рис 2.15 показано простое графическое представление нечеткого вывода в Мамдани модели.

Рис. 2.15. Графическое представление нечеткого вывода в Мамдани модели.

Нечеткая Модель Сугено

В нечеткой модели Сугено (Sugeno fuzzy model) используются следующие нечеткие правила (общий вид):

ЕСЛИ И И … И ТО

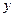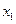где - входные переменные нечеткой модели, - выходное значение; - индекс нечеткого правила, (число нечетких правил); - множество функций принадлежности, описывающих входную переменную ; - множество функций принадлежности, описывающих входную переменную ; … - множество функций принадлежности, описывающих входную переменную .

Правая часть нечеткого правила представляется четкой полиномиальной функцией:

.

Если правая часть (константа), то такая нечеткая модель называется нечеткая модель Сугено нулевого порядка (zero-order Sugeno fuzzy model). Эта модель используется в нечетких ПИД регуляторах.

В общем виде, четкое выходное значение в нечеткой модели Сугено (с нечеткой конъюнкцией в виде умножения, синглетон - фаззификатором и дефаззификатором «взвешенное среднее») вычисляется по следующей формуле:

.

На рис. 2.16 показано простое графическое представление нечеткого вывода в Сугено модели.

Нечеткая Модель Цукамото

В нечеткой модели Цукамото (Tsukamoto fuzzy model) используются следующие нечеткие правила (общий вид):

ЕСЛИ И И … И ТО ,

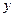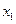где – входные переменные нечеткой модели, - выходное значение; - индекс нечеткого правила, (число нечетких правил); – множество функций принадлежности, описывающих входную переменную ; – множество функций принадлежности, описывающих входную переменную ; …, – множество функций принадлежности, описывающих входную переменную .

Рис. 2.16. Графическое представление нечеткого вывода в Сугено модели

В отличие от двух предыдущих моделей функции принадлежности , описывающие выходную переменную 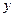, представляет собой монотонно убывающую (или монотонно возрастающую) функцию (рис. 2.17); - множество функций принадлежности, описывающих выходную переменную .

Рис. 2.17. Графическое представление нечеткого вывода в Цукамото модели

В общем виде, четкое выходное значение в нечеткой модели Сугено (с нечеткой конъюнкцией в виде умножения, синглетон-фаззификатором и дефаззификатором «взвешенное среднее») вычисляется по следующей формуле:

,

где

На рис. 2.17 показано простое графическое представление нечеткого вывода в Цукамото модели.

Рассмотренные выше модели нечеткого вывода широко используются в прикладных задачах нечеткого управления.