Тема 3. Погрешности технических измерений

Погрешность измерения – это отклонение фактического результата измерения от истинного значения измеряемой величины.

Погрешности классифицируются на виды по различным признакам:

1) по способу выражения:

а) абсолютная погрешность (выражается в единицах измеряемой величины):

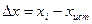или ;

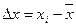б) относительная погрешность (выражается в безразмерной форме):

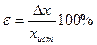или .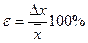

2) по характеру проявления и воздействия на результат измерения:

а) грубая погрешность;

б) систематическая погрешность;

в) случайная погрешность.

Грубая погрешность – это погрешность, которая существенно превышает ожидаемую и обусловлена неисправностью измерительных средств и неправильностью отсчета показаний и записи результатов измерений. Она влияет на среднее и поэтому должна быть выявлена и исключена.

Представляя результаты измерений в виде статистического ряда x₁, x₂, x_3, …, x_n выявляют сомнительные результаты, под которыми понимают минимальные и максимальные значения. Для проверки сомнительного результата используют критерий оценки грубой погрешности β:

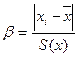
где 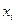– сомнительный результат;

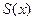- среднее квадратическое отклонение отдельных результатов измерения.

Если β ≥ β_табл (Р,n), то сомнительный результат отбрасывается (n – число наблюдений, Р- доверительная вероятность).

Систематическая погрешность - это погрешность, которая при повторных измерениях одной и той же величины либо остается постоянной, либо закономерно увеличивается. В зависимости от причин разделяют следующие виды систематических погрешностей:

1) методическая погрешность. Она обусловлена неправильными приемами использования средств измерений, некорректным округлением результата измерений;

2) субъективная погрешность. Она обусловлена индивидуальными особенностями оператора;

3) дополнительная погрешность. Обусловлена изменением внешних условий измерения, например, температуры;

4) приборная погрешность (погрешность средства измерения). Она присутствует всегда и ее необходимо учитывать, сравнивая со случайными погрешностями.

Систематические погрешности являются наиболее опасными, так как они влияют на среднее. Поэтому они должны быть обнаружены при использовании более точных средств измерений. При разработке методики измерений устанавливается источник погрешностей. Если есть возможность, этот источник исключается, например, при наладке электроизмерительного прибора, производимой с помощью ручки-установки нуля.

Если источник погрешностей исключить нельзя, то вводится поправка. Поправка – это систематическая погрешность с обратным знаком, которая прибавляется к полученному результату измерений, например, температурная поправка. Но в реальных условиях полностью исключить систематическую погрешность нельзя. В этом случае говорят: остаются неисключенные остатки систематической погрешности. К ним относится погрешность средства измерения.

Случайная погрешность – это погрешность, которая присутствует практически всегда и вызывается большим числом неконтролируемых случайных причин, действие которых заранее предсказать и исключить невозможно, например, вибрация пола. Она обнаруживается при повторном измерении одной и той же величины, когда получаются неодинаковые результаты. Случайная погрешность влияет на рассеяние измеряемой величины. Исключить случайные погрешности невозможно, но уменьшить их влияние на результат измерения можно путем увеличения числа параллельных наблюдений (измерения с многократными наблюдениями).

Измерения с многократными наблюдениями могут быть выполнены при большом или малом числе измерений.

При большом числе наблюдений (сотни, тысячи) результаты измерений представляют в виде ряда случайных чисел х_1; х_2; х₃ … х_n, который разбивается на одинаковые интервалы. Количество интервалов (к) примерно определяется следующим отношением:

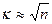
n – число наблюдений.

В каждом из интервалов подсчитывают частоту 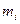появления значения измеряемой величины и строят гистограмму (столбиковая диаграмма). Для каждого интервала можно определить и относительную частоту (вероятность) m_i / n. Если относительную вероятность поделить на величину интервала, то получится плотность вероятности:

.

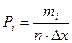Площади прямоугольников в гистограмме равны вероятности попадания измеряемой величины в конкретный интервал. При уменьшении Δх и увеличении количества интервалов гистограмма плавно переходит в кривую, которую называют графиком плотности распределения случайной величины, а уравнение описывающее его называют законом распределения случайной величины. В теории вероятностей большинство случайных величин подчиняются нормальному закону (закону Гаусса), геометрически характеризующегося колоколообразной кривой:

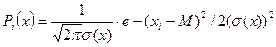
Закон Гаусса характеризуется:

- М - генеральным средним отдельных результатов наблюдений (математическим ожиданием). Он определяет центр распределения;

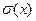- - средним квадратичным отклонением отдельных результатов измерений;

Он определяют рассеяние отдельных результатов наблюдений.

Доказано, что если систематические погрешности полностью исключены, то истинное значение измеряемой величины равно М (центр распределения).

Зная закон распределения можно определить доверительную вероятность, доверительный интервал и уровень значимости. Доверительная вероятность – это вероятность того, что результат измерения не выйдет за доверительный интервал,в котором находится истинное значение измеряемой физической величины.

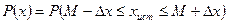- вероятность попадания величины в доверительный интервал, которая определяется интегрированием уравнения Гаусса в интервале :

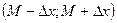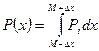
Площадь под всей кривой будет равна 1 (доверительная вероятность 100 %). Разность между единицей и Р(х) называется уровнем значимости α: α = 1- Р. В этом случае α характеризует вероятность того, что измеряемая величина не попадает в доверительный интервал. Р и α задаются справочными таблицами.

При смещении вертикальной оси Р в центр распределения получаем график распределения случайных погрешностей.

Из закона Гаусса следует, что погрешности, одинаковые по величине, но с противоположными знаками встречаются одинаково часто. К тому же, чем больше по величине погрешность, тем меньше вероятность ее появления.

Для удобства расчетов при обработке результатов наблюдений целесообразно перейти к переменной 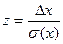. Тогда закон Гаусса представляется в форме: 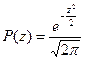(функция Лапласа), где z – значения нормированной функции Лапласа, которые определены таблично. Задавая значения z, можно определить доверительную вероятность Р и уровень значимости α:

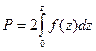
Например, z=1, то Δх=σ(х); Р=68%, α=32%;

z=2, то Δх=2σ(х); Р=95%, α=5%;

z=3, то Δх=3σ(х) – правило «трех сигм»; Р=99,7%, α=0,3%.

При ограниченном числе наблюдений (в реальных условиях технических измерений) центр распределения характеризуется средним арифметическим 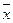, а отклонение среднего арифметического - средним квадратическим отклонением результатов измерений:

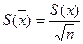, где n – число параллельных наблюдений, 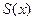- среднее квадратическое отклонением отдельных результатов наблюдений (ошибка метода измерений).

Перейдя к переменной 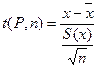, получают закон распределения измеряемой величины, называемым законом Стьюдента.

При n>30-40 (считается как большое число параллельных наблюдений) распределение Стьюдента практически переходит в нормальное (гауссовское) распределение.

При определении случайной погрешности рассматривают два варианта обработки результатов измерений:

1. погрешность метода измерений S(x) неизвестна:

В этом случае S(x) и Δх определяют по формулам:

;

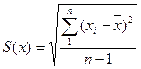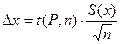
2. погрешность метода измерений S(x) известна. В этом случае Δх определяют по формуле:

.

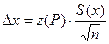Для уменьшения случайной погрешности 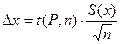либо увеличивают число параллельных наблюдений n, либо уменьшают среднее квадратическое отклонение отдельных результатов наблюдений 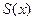, используя более точный метод измерения.

Исходя из приведенных формул можно определить необходимое число параллельных наблюдений, чтобы абсолютная погрешность результата измерения не превышала установленного значения Δх_зад. ( в соответствие с требованиями методики измерений) .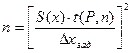

Для оценки точности технических измерений (при выборе различных технических решений) используют относительную погрешность: 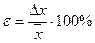. Чем меньше ε, тем выше точность измерений. За меру точности измерения принимают величину, обратную ε.

Если неисключенные остатки систематической погрешности (погрешность средства измерения 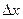_си ) близки случайным погрешностям, то определяют суммарную погрешность измерения в соответствие с правилом сложения погрешностей 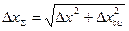, где 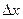_си = 3σ(х) в соответствии с правилом «трех сигм» при Р=99,7%, α=0,3%.

Определение погрешности результата измерения выполняют в соответствии с методикой измерений, под которой понимают НТД, регламентирующий совокупность операций и правил выполнения измерений, обеспечивающих качественный результат.

Под качествомизмерений понимают точность, правильность и достоверность измерений. Точностьопределяется близостью результатов измерений к истинному значению. Она обратно пропорциональна погрешности измерений и возрастает с ее уменьшением. Чем меньше погрешность, тем выше точность измерений. Правильность измерений определяется близостью к нулю неисключенной систематической погрешности (погрешности средства измерения).

Достоверность измерений определяется степенью доверия к результату и характеризуется вероятностью того, что истинное или среднее значение измеряемой величины находится в доверительных границах. Как правило, при технических и аналитических измерениях доверительная вероятность Р устанавливается равной 0,95. При назначении доверительной вероятности необходимо учитывать степень важности (ответственности) результата измерения. Если ошибка в измерении может привести к отрицательным последствиям, доверительная вероятность должна быть увеличена до 0,997. Доверительная вероятность выражается, как правило, числом от 0 до 1 или в процентах от 0 до 100%.

Результат измерения представляют в форме х =`х ± Dх, если проводятся измерения с многократными наблюдениями, или х = х ± Dх, если проводится измерения с однократными наблюдениями, где х – результат наблюдения, `х - среднее арифметическое результата измерения, Dх – случайная, систематическая (погрешность средства измерения) или суммарная погрешность измерений.

Границы доверительного интервала определяют как `х + Dх, `х - Dх или х + Dх, х - Dх. При округлении результатов измерений следует придерживаться правил округления.