Ниже приведены некоторые из основных операций, которые можно осуществлять над нечеткими множествами

1. Дополнение нечеткого множества 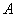обозначается символом 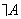(или иногда 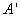) и определяется следующим образом:

(3.33)

Операция дополнения соответствует логическому отрицанию. Так, например, если 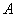— название нечеткого множества, то «не 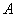» понимается как 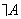(см. пример 3.8).

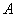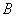2. Объединение нечетких множеств и обозначается 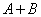(или, что более привычно, 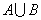) и определяется следующим образом:

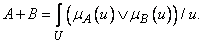(3.34)

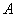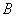Объединение соответствует логической связке «или». Так, если, например, и — названия нечетких множеств, то запись « 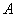или 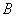» понимается как .

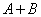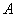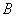3. Пересечение и обозначается 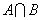и определяется следующим образом:

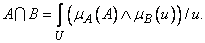(3.35)

Пересечение соответствует логической связке «и», т. е.

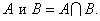(3.36)

Замечание 3.7. Следует иметь в виду, что

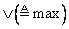и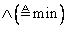

— не единственные операции, посредством которых можно определить операции объединения и пересечения (по этому вопросу см. [25] и [26]). В связи с этим важно отметить, что если операция «и» определяется с помощью операции min, как в (3.36), то она является «жесткой» в том смысле, что в ней недостаточно учитываются функции принадлежности обоих множеств. В противоположность этому операция «и», определяемая с помощью арифметического произведения, как в (3.37), является «мягкой». Какое из этих двух, а возможно, и других определений является наиболее подходящим, зависит от смысла, вкладываемого в эту операцию в каждом конкретном случае.

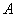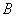4. Произведение и обозначается 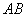и определяется формулой

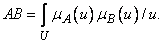(3.37)

Таким образом, любое нечеткое множество 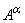, где 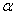— положительное число, следует понимать так:

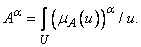(3.38)

Аналогично, если 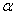— любое неотрицательное число, такое, ч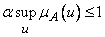то , то

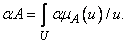(3.39)

Частными случаями операции возведения в степень [см. (3.35)] являются операция концентрирования, определяемая следующим образом

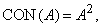(3.40)

и операция растяжения

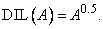(3.41)

http://tinyurl.com/byvaqt7 http://tinyurl.com/b68mgh3 http://tinyurl.com/a5vomda -примеры

Нечеткие отношения:http://tinyurl.com/aphfsg4

Операции над нечеткими отношениями:http://tinyurl.com/ak77lnr http://tinyurl.com/aa6wk5x

6.Лингвистическая переменная: определение, структура, связь с нечеткими множествами.

Лингвистическая переменная — в теории нечётких множеств, переменная, которая может принимать значения фраз из естественного или искусственного языка. Например, лингвистическая переменная «скорость» может иметь значения «высокая», «средняя», «очень низкая» и т. д. Фразы, значение которых принимает переменная, в свою очередь являются именами нечетких переменных и описываются нечетким множеством.

Лингвистическая переменная характеризуется набором свойств 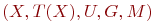, в котором:

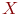— название переменной;

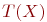обозначает терм-множество переменной 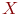, т.е. множество названий лингвистических значений переменной 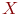, причем каждое из таких значений является нечеткой переменной 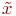со значениями из универсального множества 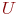с базовой переменной ;

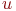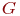— синтаксическое правило, порождающее названия 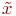значений переменной ;

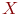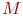— семантическое правило, которое ставит в соответствие каждой нечеткой переменной 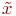ее смысл 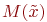, т.е. нечеткое подмножество 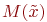универсального множества .

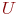Конкретное название 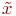, порожденное синтаксическим правилом 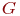, называется термом. Терм, который состоит из одного слова или из нескольких слов, всегда фигурирующих вместе друг с другом, называется атомарным термом. Терм, который состоит из более чем одного атомарного терма, называется составным термом.

Пример. Рассмотрим лингвистическую переменную с именем 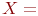"ТЕМПЕРАТУРА В КОМНАТЕ". Тогда оставшуюся четверку 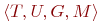, можно определить так:

универсальное множество U=[5,35];

терм-множество T={"ХОЛОДНО", "КОМФОРТНО", "ЖАРКО"} с такими функциями принадлежностями:

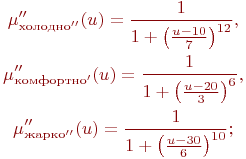
синтаксическое правило 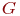, порождающее новые термы с использованием квантификаторов "и", "или", "не", "очень", "более-менее" и других;

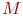будет являться процедурой, ставящей каждому новому терму в соответствие нечеткое множество из 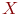по правилам: если термы 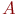и 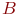имели функции принадлежност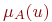и и 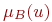соответственно, то новые термы будут иметь следующие функции принадлежности, заданные в таблице:

Квантификатор	Функция принадлежности ( )
не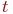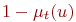
очень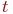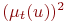
более-менее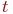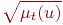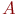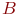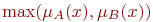
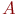и
или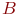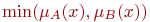

http://tinyurl.com/b7mwwkn -продолжение http://tinyurl.com/acdh4cf -дополнение