Представления булевых функций разложениями по переменным

Множества и отношения.

Множества и их спецификации. Операции над множест-вами. Диаграммы Эйлера-Венна. Мощность множества. Конеч-ные и счетные множества. Отношения. Свойства отношений. Операции над отношениями. Отношение эквивалентности. Раз-биения и отношение эквивалентности. Отношения частичного и строгого порядка. Функции и отображения. Инъекция, сюръекция, суперпозиция, биекция, обратные функции.

Литература: [1], с. 5-10; [3], часть 2; [4], гл. 1-3; [5], гл. 1.

Булевы алгебры. Элементы математической логики.

Булевы функции. Способы задания. Существенные и фиктивные переменные. Булевы формулы. Основные свойства логических операций. Совершенные нормальные формы. Поли-ном Жегалкина. Замкнутые классы функций. Функционально полные системы. Теоремы о функциональной полноте. Примеры функционально-полных базисов. Проблема минимизации булевых функций. Схемы из функциональных элементов. Конечные автоматы. Формальные теории. Понятие высказыва-ния. Тавтологии. Исчисление высказываний. Логика предикатов.

Литература:[1], с. 14-53; [2], гл. 3,8; [3], части 1,4; [4], гл. 4, 5; [5], гл. 3,4.

Эквивалентность булевых формул.

Булевы функции могут быть заданы либо с помощью таблиц истинности (единственным образом), либо с помощью логических формул (неединственным образом). Если таблицы истинности двух булевых формул совпадают, то эти формулы эквивалентны и определяют одну и ту же булеву функцию.

Пример.Проверить эквивалентность булевых формул:

.

Построим таблицу истинности для функции .

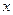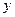Построим таблицу истинности для функции

.

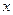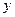Результирующие столбцы в таблицах истинности совпадают, следовательно, формулы эквивалентны.

Существенные и фиктивные переменные.

Переменная ( ) булевой функции называется фиктивной, если имеет место равенство

для любых значений переменных . В против-ном случае переменная называется существенной. Наборы значений переменных в последнем равенстве называются соседними по переменной .

Пример.Определить существенные и фиктивные переменные функции (11110011).

Для удобства приведем таблицу истинности.

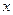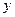Проверим, является ли переменная 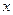существенной или фиктивной. Рассмотрим значения функции на наборах, соседних по переменной :

,

.

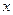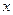. Значит, переменная – существен-ная.

Рассмотрим теперь значения функции на наборах, сосед-них по переменной :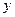

, .

, .

, .

. Следовательно, переменная 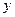– су-щественная.

Рассмотрим значения функции на наборах, соседних по переменной :

, .

, .

, .

, .

На всех парах соседних по переменной наборов значе-ний переменных функция принимает равные значения, следова-тельно, переменная – фиктивная.

Представления булевых функций разложениями по переменным.

Совершенная дизъюнктивная нормальная форма (СДНФ) для булевой функции , не равной тождест-венно нулю, имеет вид:

,

где символ определяется следующим образом:

Алгоритм построения СДНФ.

1. Построить таблицу истинности данной булевой функции.

2. Каждому единичному значению булевой функции будет соответствовать элементарная конъюнкция 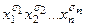, где 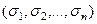– соответствующий набор значений перемен-ных. В конъюнкции мы записываем , если , и , если . Конъюнкции соединяются знаком .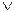

Совершенная конъюнктивная нормальная форма (СКНФ) для функции , отличной от тождественной единицы, имеет вид:

.

Алгоритм построения СКНФ.

1. Построить таблицу истинности данной булевой функции.

2. Каждому нулевому значению булевой функции будет соответствовать элементарная дизъюнкция , где 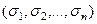- соответствующий набор значений переменных. В дизъюнкции мы записываем , если , и , если . Дизъюнкции соединяются знаком .

Всякая булева функция может быть представлена в виде полинома Жегалкина:

где , где знак 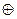обозначает сумму по модулю 2.