Понятие вариации и ее значение

Вариация –

То колеблемость, многообразие, изменяемость величины признака у единиц совокупности.

Значение вариации. Исследование вариации дает возможность оценить степень воздействия на данный признак других варьирующих признаков.

Меры вариации

· Абсолютные

1. Размах вариации

2. Среднее линейное отклонение

3. Дисперсия

4. Среднее квадратическое отклонение

· Относительные

1. Коэффициент осцилляции

2. Коэффициент вариации

3. Отклонение линейное относительно

6.1. Абсолютные показатели вариации

Размах вариации

Где: – максимальное значение признака в совокупности;

– минимальное значение признака в совокупности/

Недостатки показателя:

Сильно зависит от максимальных, часто – аномальных значений;

Не учитывает «внутреннею» вариацию между границами.

Среднее линейное отклонение

– невзвешенная форма

– взвешенная форма

При расчете среднего линейного отклонения осредняется модулей индивидуальных отклонения, так как

- взвешенная

– невзвешенная

Дисперсия и среднее квадратическое отклонение

– невзвешенная форма

– взвешенная форма

Дальше формулы могут быть приведены к выражению вида :

Чем сильнее колеблемость признаков, тем больше отклонение его значения от средней величины и менее устойчив изучаемый признак

Доказательство:

Ср. квадратич. Отклонение – корень квадр. Из дисперсии

Коэффициент осцилляции

Линейный коэффициент вариации

Коэффициент вариации

Позволяет оценить однородность совокупности по одному иди нескольким признакам: если V<33%, то совокупно можно считать однородной.

Условие задачи:

Вариация альтернативных признаков

p – доля единиц, обладающих признаком.

q – доля единиц, не обладающих данными признаками p + q = 1

Сложение дисперсии изучаемого признака.

3 вида дисперсий

· Общая дисперсия характеризует вариацию признака в целом по совокупности

· Межгрупповая – вариацию групповых средних

· Внутригрупповые – вариацию индивидуальных значений относительно групповых средних.

Общая дисперсия – измеряет вариацию признака под влиянием всех факторов.

Внутригрупповая дисперсия – отражает случайную вариацию, т.е. под влиянием неучтенных факторов.

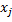– отдельные значения признака в каждой группе

– это среднее значение признаков в каждой группе

– это численность каждой группы

6.5 Использование показателей вариации в анализе взаимосвязей

Межгрупповая дисперсия -

Где: - среднее значение признака по i-й группе;

- объем (численность единиц) i-й группы;

k - число групп, на которые разделена совокупность;

- среднее значение признака, по всей совокупности

Данный показатель отражает ту часть общей дисперсии, которая обусловлена действием учтенного фактора, положенного в основание группировки.

По совокупности в целом вариация значений признака, под влиянием прочих факторов характеризуется средней из внутри-групповых дисперсий.

Средняя из внутригрупповых дисперсий

Где: - дисперсия изучаемого признака в i-й группе;

- объем (численность единиц) i-й группы;

K - число групп , на которые разделена совокупность.

Данный показатель отражает ту часть общей дисперсии, которая обусловлена действием всех факторов, кроме фактора, положенного в основание группировки.

Правило сложения дисперсий

Где: - общая дисперсия признака по всей совокупности, без учета деления этой совокупности на группы;

- средняя из внутригрупповых дисперсий;

- межгрупповая дисперсия.

Эмпирическое корреляционное отношение

Является количественной оценкой влияния факторного признака на вариацию признака результативного. Принимает значения от 0 до +1.

Эмпирический коэффициент детерминации

Показывает долю общей дисперсии изучаемого признака, обусловленную фактором, положенным в основание группировки.

(тут далее идут примеры на доске, ребят не осилил в paint J .)