Упражнения. 4.4.1. Решите задачу: Определите расстояние Хемминга между словами A и B и установите, сколько такой может обнаружить ошибок и сколько исправить: а) A

4.4.1. Решите задачу: Определите расстояние Хемминга между словами A и B и установите, сколько такой может обнаружить ошибок и сколько исправить:

а) A =(001101) B = (010101)	б) A = (011011) B = (010100)
в) A = (010111) B = (010101)	г) A = (100001) B = (010100)
д) A = (100010) B = (010101)	е) A = (001010) B = (010100)
ж) A = (010110) B = (010101)	з) A = (001001) B = (010100)
и) A = (011000) B = (010101)	к) A = (011100) B = (010100)

Образец: Определите расстояние Хемминга между словами A= (01001101) и B=(01011011) и установите, сколько такой может обнаружить ошибок и сколько исправить.

Решение: 1) Для определения расстояние Хемминга между словами A и B сравним их позиции поразрядно. Имеем несовпадение во втором, третьем и пятом разрядах (считая справа налево), т.е. d(A,B)=3. Результат можно проверить с помощью М2 (сложения по модулю 2): В нашем примере С=А 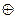В=10101000, т.к.

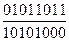+ . Тогда V(С)=d (А,В)= .

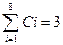2)Т.к.минимальное расстояние между кодовыми словамиd(A,B)=3, то число ошибок, которые способен обнаружить этот код, можно найти согласно неравенству d(b_i,b_j)³ k+1.Тогда имеем 3³ k+1. Отсюда видно, что код сможет обнаружить не более двух ошибок.

3) Такой код, согласно неравенству d(b_i,b_j)³ 2 k+1,сможет устранить не более, чем 3³ 2k+1ошибок. В итоге при k=1он может устранить не более одной ошибки.

4.4.2.Определите расстояние Хемминга произвольного кода, заданного в задании 4.3.8.

Образец: a₁=100, а₂=0111, а₃=010, а₄=0000, а₅=0101, а₆=1011, а₇=01.

Решение: Схема кода имеет вид:

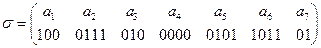. Найдем минимальное расстояние d(а_i, а_j ), где i¹j,между попарно взятыми заданными кодовыми словами:

а₁Åа₂ =100Å0111=1011, d(а₁, а₂ )= ;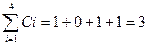

а₁Åа₃ =100Å010=110, d(а₁,а₃)= 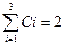; а₁Åа₄ =100Å0000=0100, d(а₁,а₄)= 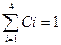, и т.д. Очевидно, минимальное расстояние d(а_i, а_j) =1.

4.4.3.Покажите, что матрица М =(А,Е) является проверочной матрицей кода Хемминга.

.

а)	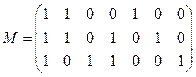б)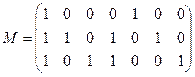
в)	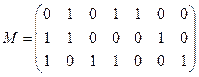г)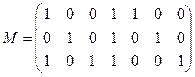
д)	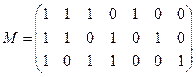е)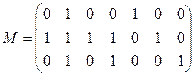
ж)	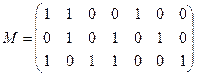з)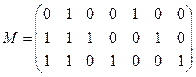
и)	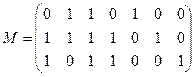к)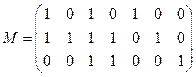

Образец: Покажите, что матрица

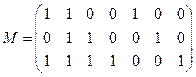является проверочной матрицей кода Хемминга.

Решение: Из матрицы М =(А Е) порядка 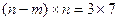получим значения n=7 и m=4. Последние три столбца образуют единичную матрицу 3-го порядка 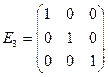. Первые четыре столбца матрицы М соответствуют матрице А порядка 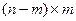. Отсюда при n-m=7-4=3 матрица А порядка 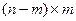= 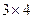имеет вид: 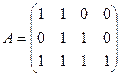. Первые четыре столбца матрицы М, соответствующие матрице А, представляют собой двоичную запись чисел 5, 7, 3, 1.

Значит, заданная матрица М =(А,Е) является проверочной матрицей (4,7) кода Хемминга.

4.4.4.Получите порождающуюматрицу кода Хемминга для матрицы в задании 4.4.2. Сколькотакой код может обнаружить ошибок и сколько исправить.

Образец: Получите порождающуюматрицу кода Хемминга для матрицы

.

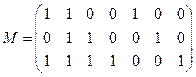Решение: 1) Задана проверочная матрица М кода Хемминга размерности .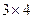

В порождающей матрице М должна присутствовать единичная матрица порядка m=4, т.е. 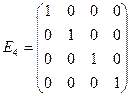, а также матрица 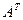– полученная транспонированием матрицы A. Если 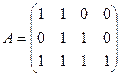, то соответствующая транспонированная матрица имеет вид .

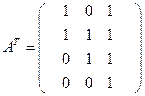2) Построим 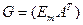– порождающуюматрицу кода Хемминга для матрицы M m=4, которая содержит 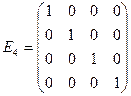и .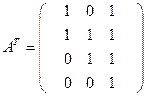

Отсюда имеем 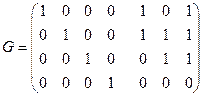. Порождающаяматрица 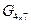при m=4 и n=7 задает (4, 7)-код Хемминга, в котором первые четыре разряда информационные, а последние k=n-m=7-4=3 – контрольные.