Практическое представление результатов эксперимента эмпирическими формулами
При использовании ЭВМ можно значительно упростить и автоматизировать представление уравнения регрессии эмпирическими формулами [11], выбрав некоторый класс функций (из заранее заданного многообразия), соответствующий по своему характеру исследуемому физическому процессу.
Для этого необходимо:
1) выбрать некоторый класс функций (из заранее заданного многообразия), соответствующий по своему характеру исследуемому физическому процессу.
2) произвести переход к новым переменным, соответствующим заданным классам функций, и вычислить для каждого опытного значения исходных данных новые (пересчитанные) значения.
3) вычислить аппроксимирующие полиномы для пересчитанных значений опытных данных, используя в качестве промежуточного звена подпрограмму вычисления ортогональных полиномов методом наименьших квадратов [12].
4) произвести обратный переход к старым переменным.
5) вычислив критерии адекватности уравнения регрессии, сравнить их между собой для каждого многообразия и выбрать оптимальный вариант.
В результате получим уравнение регрессии в виде эмпирической формулы от некоторого количества параметров, которые будут тождественно равны коэффициентам промежуточного аппроксимирующего полинома.
В таблице 11 приводится вид 26 классов функций и соответствующие им преобразования координат, используемых в подпрограмме FUNC [12].
Число "n" означает степень промежуточного аппроксимирующего полинома и соответствует (n+1) параметрам.
Количество классов функции при необходимости можно увеличить.
Данный метод реализован в программе AF [12].
Примечание: * Следует отметить, что приведенный метод оценивания параметров, установления их оптимальности, не является наилучшим в широком смысле для всех классов функций ввиду нелинейности преобразований. Однако для практических целей такое оценивание параметров в заданном узком классе функций вполне достаточно и дает хороший результат.
Таблица 11
Классы функций и соответствующие им преобразования координат
| №№ пп | Преобразованные переменные | Конечный вид функции | ||
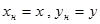 | 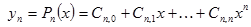 | |||
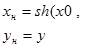 | 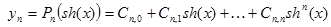 | |||
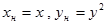 | 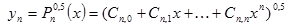 | |||
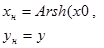 | 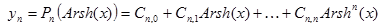 | |||
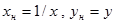 | 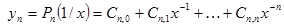 | |||
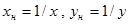 | 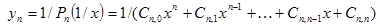 | |||
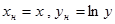 | 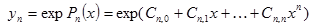 | |||
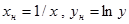 | 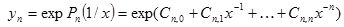 | |||
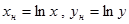 | 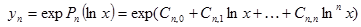 | |||
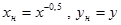 | 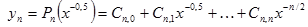 | |||
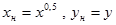 | 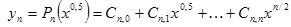 | |||
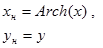 | 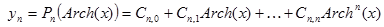 | |||
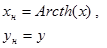 | 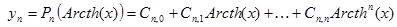 | |||
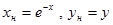 | 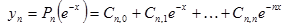 | |||
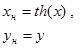 | 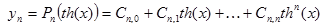 | |||
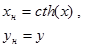 | 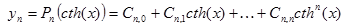 | |||
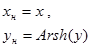 | 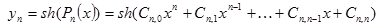 | |||
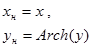 | 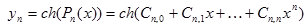 | |||
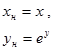 | 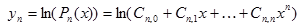 | |||
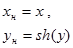 | 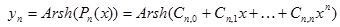 | |||
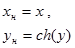 | 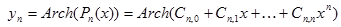 | |||
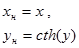 | 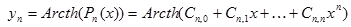 | |||
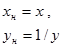 | 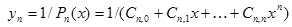 | |||
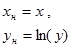 | 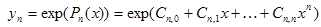 | |||
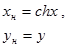 | 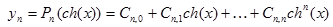 | |||
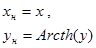 | 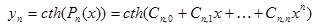 | |||
