Расчетно-графическая работа №2. Стандартная обработка результатов однократных прямых и косвенных измерений
Цель работы: изучение способов обработки и правильного представления результатов однократных прямых и косвенных измерений.
Задание №1
2.1.1 Прямые однократные измерения
Подавляющее большинство измерений, выполняемых на практике, являются однократными. Прежде чем выполнить однократное измерение, необходимо выбрать средство измерения, исходя из представления об условиях проведения измерения, о свойствах измеряемой величины и ее примерном значении, о необходимой точности измерения, а также определяют с помощью какого измерительного прибора, какого типа, какого класса точности, на каком пределе шкалы лучше проводить измерение.
За результат однократного измерения принимают показания средства измерения. Результирующая погрешность однократного измерения в общем случае зависит от целого ряда факторов, в частности, от инструментальной и методической составляющих погрешности, влияния внешних воздействий и т.д. Точность результата прямого измерения при применении измерительного показывающего прибора прямого действия может быть оценена приближенной максимальной (или предельной) погрешностью, определяемой по формуле
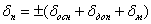 , (2.1)
, (2.1)
где 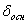 - пределы допускаемой основной погрешности применяемого измерительного прибора при его эксплуатации в нормальной области значений влияющих величин;
- пределы допускаемой основной погрешности применяемого измерительного прибора при его эксплуатации в нормальной области значений влияющих величин;
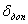 - пределы допускаемых дополнительных погрешностей измерительного прибора, определяемые отклонением влияющих величин за пределы, установленные для их нормальных значений или для нормальной области значений;
- пределы допускаемых дополнительных погрешностей измерительного прибора, определяемые отклонением влияющих величин за пределы, установленные для их нормальных значений или для нормальной области значений;
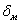 - методическая погрешность.
- методическая погрешность.
При проведении однократных измерений всегда стремятся поддерживать нормальные условия эксплуатации и выбрать такой способ измерений, чтобы методическая погрешность и субъективные погрешности оказывали минимальное воздействие на результат.
Если однократное измерение правильно организовано, то для представления результатов измерений достаточно, как правило, сведений о показании средства измерений и пределах его допускаемой основной погрешности, для определения которой используется такая метрологическая характеристика, как класс точности средства измерений.
Формулы вычисления пределов основной погрешности средств измерений и примеры обозначения для их классов точности приведены в таблице 1.
Т а б л и ц а 1- Формулы для вычисления предела основной погрешности
| Формула для вычисления предела основной погрешности | Пределы допускаемой основной погрешности, % | Примеры обозначения класса точности средства измерений Общий вид пример |
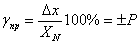 | 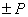 | Р 2,5 |
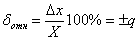 | 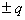 |    |
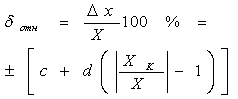 | 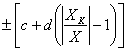 | 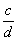 0,02/0,01 0,02/0,01 |
В таблице 1: Х – показание средства измерений; 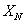 - нормирующее значение, равное диапазону измерения для данного средства измерений;
- нормирующее значение, равное диапазону измерения для данного средства измерений; 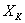 - конечное значение выбранного диапазона измерений;
- конечное значение выбранного диапазона измерений; 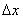 - абсолютная погрешность средства измерений. Величины P, q, c, d представляют собой числа, выбираемые из ряда (1; 1,5; 2; 2,5; 3; 4; 5; 6) 10
- абсолютная погрешность средства измерений. Величины P, q, c, d представляют собой числа, выбираемые из ряда (1; 1,5; 2; 2,5; 3; 4; 5; 6) 10 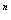 , где n=1; 0; -1; -2 и т.д.
, где n=1; 0; -1; -2 и т.д.
2.1.2 Правила округления результата измерения
Результат измерения записывается в виде
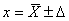 , Р, (2.2)
, Р, (2.2)
где 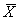 - собственно результат измерения (или среднее арифметическое значение);
- собственно результат измерения (или среднее арифметическое значение);
 - погрешность (или доверительные границы погрешности) результата измерения;
- погрешность (или доверительные границы погрешности) результата измерения;
Р – доверительная вероятность.
Эта форма представления результата измерений принята в качестве основной при оценке точности измерений в АСУ ТП энергетики.
При окончательном оформлении результатов измерений необходимо придерживаться следующих правил.
Поскольку погрешности измерений определяют лишь зону неопределенности результатов, их не требуется знать очень точно. В окончательной записи погрешность измерения принято выражать числом с одним или двумя значащими цифрами. Эмпирически были установлены следующие правила округления рассчитанного значения погрешности и полученного результата измерения:
1. Округление результата измерений начинают с округления значения погрешности; затем округляют значение собственно результата измерения.
2. Погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2, и одной цифрой, если первая цифра равна 3 или более.
3. Результат измерения округляется до того же десятичного знака, которым оканчивается округленное значение абсолютной погрешности.
4. Если цифра старшего из отбрасываемых разрядов меньше 5, то остальные цифры числа не изменяются. Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются.
5. Если цифра старшего из отбрасываемых разрядов больше 5, то последнюю оставляемую цифру увеличивают на единицу.
6. Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или нули, то последнюю сохраняемую цифру числа не изменяют, если она четная, и увеличивают на единицу, если она нечетная. Если цифра старшего из отбрасываемых разрядов равна 5, но за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на единицу.
7. Округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним-двумя лишними знаками.
Если руководствоваться этими правилами округления, то количество значащих цифр в числовом значении результата измерений дает возможность ориентировочно судить о точности измерения. Это связано с тем, что предельная погрешность, обусловленная округлением, равна половине единицы последнего разряда числового значения результата измерения.
2.1.3 Задача №1
Определить результат однократных измерений, если измерение проводилось в нормальных условиях и методическая погрешность была пренебрежительно мала. Результат измерения записать в соответствии с правилами округления (п.2.1.1.1).
Варианты индивидуальных заданий приведены в Приложении Б, таблица Б1.
2.1.3.1 Пример решения задачи №1
Указатель отсчетного устройства вольтметра, имеющего верхний предел измерения 60 мВ, показывает 30 мВ, класс точности прибора 0,02/0,01. Определить результат однократных измерений вольтметра, если измерение проводилось в нормальных условиях и методическая погрешность была пренебрежительно мала.
Решение. Поскольку класс точности задан в виде 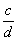 = 0,02/0,01, следовательно, для данного прибора предел основной погрешности, согласно таблице 1, вычисляется по формуле основной относительной погрешности
= 0,02/0,01, следовательно, для данного прибора предел основной погрешности, согласно таблице 1, вычисляется по формуле основной относительной погрешности
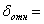
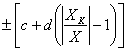 =
= 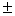
 0,03%.
0,03%.
С другой стороны, 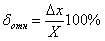 = 0,03%, отсюда предел основной абсолютной погрешности вольтметра не превышает
= 0,03%, отсюда предел основной абсолютной погрешности вольтметра не превышает 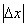
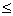 0,0003*30 мВ = 0,009мВ.
0,0003*30 мВ = 0,009мВ.
Ответ: Результат однократных измерений можно записать в виде
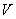 = (30,000
= (30,000 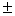 0,009) мВ.
0,009) мВ.
2.1.4 Задача №2
Выбрать класс точности и диапазон измерения для заданного средства измерения. Определить результат измерения, если измерение проводилось в нормальных условиях и методическая погрешность была пренебрежительно мала. Результат измерения записать в соответствии с правилами округления (п.2.1.1.1).
Варианты индивидуальных заданий приведены в Приложении Б, таблица Б2.
2.1.4.1 Пример решения задачи №2
Выбрать класс точности и диапазон измерения вольтметра для измерения номинального напряжения 220 В с относительной погрешностью, не превышающей 1%. Записать результат измерения, если вольтметр показал 230 В, измерение проводилось в нормальных условиях и методическая погрешность была пренебрежительно мала.
Решение. Поскольку номинальное значение параметра должно попадать во вторую половину диапазона измерений вольтметра, выбираем вольтметр с диапазоном измерения от 0 В до 300 В. Исходя из приведенного условия, для того чтобы относительная погрешность измерения не превысила 1% необходимо, чтобы модуль абсолютной погрешности измерений не превысил
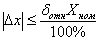 =
= 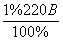 =2.2 В.
=2.2 В.
Модуль приведенной погрешности вольтметра не может превысить
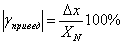 =2,2 В/300 В * 100% = 0,7%,
=2,2 В/300 В * 100% = 0,7%,
что соответствует классу точности 0,7. Приборы такого класса точности не выпускаются. Величины класса точности представляют собой числа, выбираемые из ряда (1; 1,5; 2; 2,5; 3; 4; 5; 6) 10 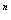 , где n=1; 0; -1; -2 и т.д. Поэтому выбираем вольтметр класса точности 0,6. Тогда модуль абсолютной погрешности измерений не превысит
, где n=1; 0; -1; -2 и т.д. Поэтому выбираем вольтметр класса точности 0,6. Тогда модуль абсолютной погрешности измерений не превысит
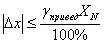 =
= 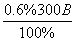 =1,8 В.
=1,8 В.
Ответ: Результат измерений записывается в виде
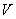 = (230,0
= (230,0 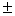 1,8) В.
1,8) В.
Задание №2
2.2.1 Методика обработки косвенных однократных измерений
Косвенные измерения – измерения, при которых искомое значение величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям
У = f (х1, х2, ..., х 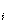 ,… , хm),
,… , хm),
х 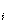 – определяют в ходе прямых измерений.
– определяют в ходе прямых измерений.
Другими словами, искомое значение физической величины рассчитывают по формуле, а значения величин, входящих в формулу, получают в ходе прямых измерений.
Пример - измерение мощности, рассеиваемой на сопротивлении, может быть выполнено расчетом по формуле 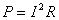 на основании измерения тока 1 и сопротивления резистора R; измерение плотности - по массе и объему тела; измерение сопротивления - по напряжению и току и т. д.
на основании измерения тока 1 и сопротивления резистора R; измерение плотности - по массе и объему тела; измерение сопротивления - по напряжению и току и т. д.
Если величины х 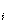 независимы, то зависимость погрешности результат измерения от погрешности исходных величин выражается формулами:
независимы, то зависимость погрешности результат измерения от погрешности исходных величин выражается формулами:
а) абсолютной погрешности
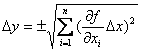
б) относительной погрешности
 .
.
2.2.2 Задача №3
При измерении расхода калориметрическим расходомером измерение мощности нагревателя производится по показаниям амперметра и вольтметра. Оба эти прибора имеют класс точности Кл=0,5, работают в нормальных условиях и имеют соответственно шкалы 0-5 А и 0-30 В. Номинальные значения силы тока 3.5 А и напряжения 24 В.
Оценить погрешность, с которой производится измерение мощности. Представить результат измерения мощности нагревателя в соответствии с правилами округления (п.2.1.1.1).
Варианты индивидуальных заданий приведены в Приложении Б, таблица Б3.
2.2.2.1 Пример решения задачи №3
Погрешность измерения мощности нагревателя W оценивается как погрешность косвенного измерения по формуле
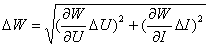 .
.
В связи с отсутствием каких-либо других метрологических характеристик средств измерений, кроме класса точности, можно определить только пределы допускаемых значений погрешности в соответствии с классом точности (Кл) и шкалой прибора (U 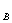 - U
- U  )
)
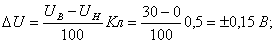
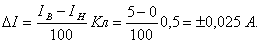
Известно, что мощность равна 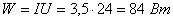 ,
,
тогда 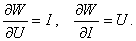
Предел допускаемой абсолютной погрешности измерения мощности
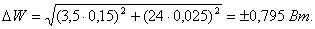
Предел допускаемой относительной погрешности измерения мощности
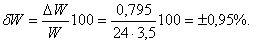
Ответ: 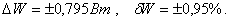
Результат измерения 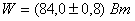 .
.
2.2.3 Задача №4
При исследовании теплоотдачи от трубы к воздуху коэффициент теплоотдачи подсчитывается из выражения
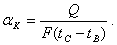
Количество теплоты Q, передаваемой трубкой путем конвекции, определяется по мощности, потребляемой электронагревателем, как произведение сопротивления трубки R на квадрат силы тока I 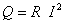 .
.
Сила тока измеряется амперметром со шкалой 0-50 А класса 0,1 , номинальное значение тока 42 А. Основная погрешность измерения силы тока не должна превышать 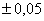 А.
А.
Зависимость сопротивления трубки от температуры была найдена в специальных опытах и описывается выражением
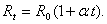 (2.1)
(2.1)
При t=0 значение сопротивления R 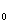 =0,5 Ом,
=0,5 Ом, 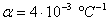 . Погрешность измерения сопротивления не превышает
. Погрешность измерения сопротивления не превышает 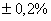 .
.
Поверхность трубки F определяется по длине l и его диаметру d
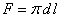 .
.
Значение длины l = 100 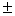 0,5 мм, диаметра d = 10
0,5 мм, диаметра d = 10 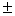 0,01 мм.
0,01 мм.
Температура стенки трубки 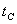 измеряется стандартным термоэлектрическим термометром градуировки ХК. Термометр через сосуд свободных концов подсоединяется к лабораторному потенциометру ПП-63 класса 0,05. Номинальное значение температуры стенки 200
измеряется стандартным термоэлектрическим термометром градуировки ХК. Термометр через сосуд свободных концов подсоединяется к лабораторному потенциометру ПП-63 класса 0,05. Номинальное значение температуры стенки 200 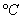 . Предел допускаемой погрешности , мВ, потенциометра ПП-63 определяется по формуле
. Предел допускаемой погрешности , мВ, потенциометра ПП-63 определяется по формуле
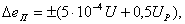
где U – показания потенциометра, мВ;
U 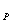 - цена деления шкалы, мВ.
- цена деления шкалы, мВ.
U 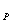 =0,05 мВ.
=0,05 мВ.
Температура воздуха 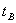 измеряется вдали от трубки ртутным термометром повышенной точности со шкалой 100 – 150
измеряется вдали от трубки ртутным термометром повышенной точности со шкалой 100 – 150 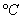 и ценой деления 0,2
и ценой деления 0,2 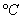 . Номинальное значение температуры воздуха составляет 120
. Номинальное значение температуры воздуха составляет 120 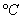 .
.
Оценить погрешность измерения коэффициента теплоотдачи на лабораторной установке. Погрешностями, связанными с методами измерения, пренебречь. Результат измерения записать в соответствии с правилами округления (п.2.1.1.1).
Варианты индивидуальных заданий приведены в Приложении Б, таблицы Б4, Б5 и Б6.
2.2.3.1 Пример решения задачи №4
Коэффициент теплоотдачи определяется как результат косвенных измерений параметров Q, F, 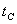 и
и 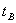 . Поэтому предел допускаемой абсолютной погрешности определения коэффициента теплоотдачи может быть подсчитан из выражения
. Поэтому предел допускаемой абсолютной погрешности определения коэффициента теплоотдачи может быть подсчитан из выражения
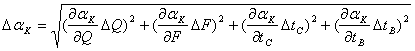 .
.
В связи с тем, что все измеряемые параметры определяются с допускаемыми отклонениями, которые можно считать предельными значениями погрешности, сам коэффициент теплоотдачи может быть оценен с каким-то пределом допускаемой погрешности.
Количество теплоты Q определяется по мощности электронагревателя. Таким образом, Q в свою очередь является результатом косвенных измерений I и R.
Температура трубки измерялась стандартным термоэлектрическим термометром градуировки ХК в комплекте с потенциометром ПП-63. Допускаемое отклонение термо-ЭДС термоэлектрического термометра ТХК от градуировочных значений при 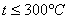 составляет
составляет 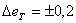 мВ (см. табл.4-7-3 [1]). Предел допускаемой погрешности потенциометра ПП-63
мВ (см. табл.4-7-3 [1]). Предел допускаемой погрешности потенциометра ПП-63
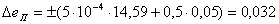 мВ;
мВ;
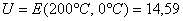 мВ.
мВ.
Оценим предел суммарной погрешности 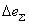 измерения температуры в предположении, что погрешности термометра и потенциометра являются независимыми величинами. Тогда
измерения температуры в предположении, что погрешности термометра и потенциометра являются независимыми величинами. Тогда
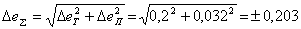 мВ,
мВ,
что соответствует 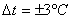 или
или 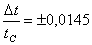 .
.
Сопротивление трубки R определялось по измеренной температуре в соответствии с выражением (2.1)
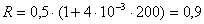 Ом.
Ом.
Погрешность определения значения R обусловлена погрешностью прибора, измеряющего сопротивление, и погрешностью измерения температуры. Составляющая погрешности, обусловленная погрешностью прибора, не превышает
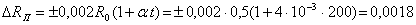 Ом.
Ом.
Составляющая погрешности, обусловленная погрешностью измерения температуры, не превышает
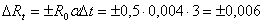 Ом.
Ом.
Оценим предел суммарной погрешности определения сопротивления нагреваемой трубки по ее температуре, полагая, что погрешность градуировки трубки и погрешность измерения температуры – независимые величины
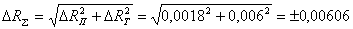 Ом
Ом
или в относительных величинах 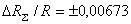 .
.
Теперь можно оценить погрешность определения количества теплоты, передаваемой от трубки к воздуху
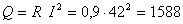 Вт,
Вт,
откуда
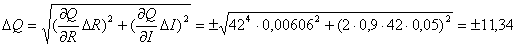 Вт.
Вт.
Оценим предел погрешности определения поверхности теплообменника F
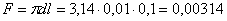 м
м 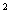 ;
;
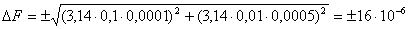 м
м 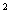 .
.
Оценим погрешность измерения воздуха по характеристикам стеклянного термометра. Термометр с ценой деления 0,2 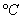 и со шкалой 100 – 150
и со шкалой 100 – 150 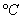 имеет предел допускаемой погрешности
имеет предел допускаемой погрешности 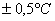 . Таким образом
. Таким образом 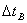 =
= 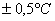 или
или 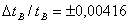 .
.
Для оценки предела погрешности определения коэффициента теплоотдачи воспользуемся формулой для определения абсолютной погрешности. Вначале определим производные
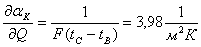 ;
;
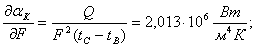
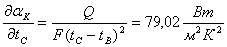 ;
;
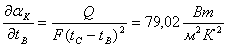 ;
;
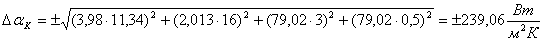 .
.
Расчетный коэффициент теплоотдачи
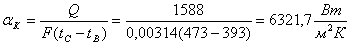 .
.
Предел допускаемой относительной погрешности
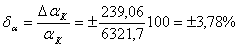 .
.
Ответ: 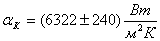 ,
, 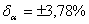 .
.
