Классификация материалов по их реологическому поведению

Ньютоновские жидкости

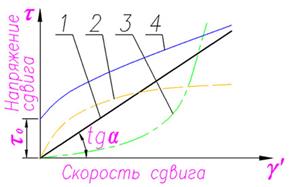
Жидкость, описываемая законом Ньютона, называется ньютоновской жидкостью. В графическом виде она представлена прямой линей (рис.2 прямая 1), исходящей из начала координат. Любая точка на этой прямой определяется двумя величинами: τ и γ’. Tg(α) показывает отношение напряжения к скорости сдвига, он является постоянной величиной на всей прямой и определяет величину вязкости.

Неньютоновские жидкости делятся на три больших группы:

a) Вязкие, или стационар­ные, неньютоновские жидкости.

b) Тиксотропные и реопектантные жидкости

c) Вязкоупругие жидкости

Кривые течения	Кривые вязкости
Рис.2. Зависимость скорости от напряжения для различных типов жидкостей	Рис.3. Зависимость скорости от вязкости для различных типов жидкостей
1- ньютоновская жидкость 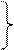Неньютоновские стационарные жидкости 2 – псевдопластичная жидкость 3 – дилатантная жидкость 4 – бингамовская пластичная жидкость

Ротационные вискозиметры.

Для оценки свойств жидкости, принадлежности ее к какой либо группе, а так же определения ее реологических характеристик применяется ряд методов с использованием приборов называемых вискозиметрами или реометрами. Реометром называется прибор позволяет определять еще какие либо реологические характеристики материала кроме вязкости.

Если обе параллельных плоскости в Ньютоновской модели (рис.1.) изогнуть, что бы они превратились в два цилиндра - внешний и внутренний, то получится измерительная ячейка ротационного вискозиметра с двумя коаксиальными цилиндрами. Пространство между цилиндрами заполняется исследуемой жидкостью, после чего она подвергается сдвигу. Измерения на данном типе вискозиметров позволяют получить данные о скоростях, напряжениях сдвига и вязкости жидкости.

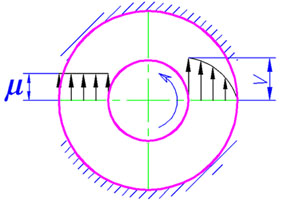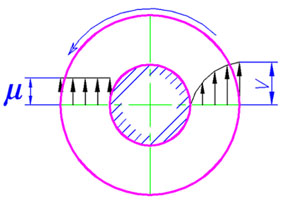Рис.1. Профили скорости и вязкости в измерительных системах Серле и Куэтта

Ротационный вискозиметры с коаксиальными цилиндрами принципиально делятся на два типа: вискозиметр действующий по измерительной системе Серле и вискозиметр действующий по измерительной системе Куэтта.

Система Серле. В случае измерительной системы Серле сдвиг жидкости осуществляется вращением внутреннего цилиндра, внешний цилиндр при этом жестко закреплен и остается неподвижным. Приборы донного типа различаются по способу задания напряжения и скорости сдвига. Измерения в вискозиметрах такого типа производится при постоянной скорости либо при постоянном напряжении сдвига.

CS-реометры. В случае измерения при заданном напряжении сдвига, в результате получаем данные о скорости сдвига. Такие приборы называют реометрами с контролируемым напряжением – CS реометры (Рис.2.).

Измерительная система Серле (вращается ротор)	Измерительная система Куэтта (вращается цилиндр)
CS (задаем напряжение)	CR (задаем скорость сдвига)
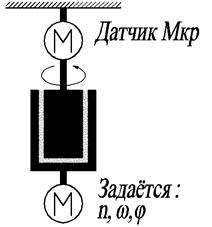Рис. 2. CS реометр системы Серле	Рис.3.CR реометр – Серле	Рис.4.CR реометр – Куэтта

Момент вращения в CS реометрах предварительно задается напряжением и силой тока подаваемыми на двигатель. Сдвигающее напряжение линейно зависит от изменяющихся на двигателе электрических величин. Наружный цилиндр может иметь рубашку для точной регуляции температуры.

Исходя из заданного крутящего момента и полученных данных о частоте вращения ротора, оценивают напряжение и скорость сдвига, после рассчитывают вязкость.

С помощью приборов такого типа возможно измерять вязкоупругие характеристики твердообразных и жидких тел.

CR-реометры. Если измерение происходит при заданной скорости сдвига, в результате определяется напряжение. Данные приборы называют CR реометрами или реометрами с контролируемой скоростью сдвига (Рис.3.).

Скорость вращения цилиндра в данном реометре постоянна или изменяется по заданной программе. Сопротивление жидкости вызывает крутящий момент на внутреннем цилиндре. Датчик кручения установлен между валом привода и валом внутреннего цилиндра. В качестве датчика используют пружины и по углу ее закручивания вычисляют крутящий момент. Наружный цилиндр может иметь рубашку для точной регуляции температуры.

Недостаток прибора: возникновение турбулентного течения низковязких жидкостей при высоких скоростях сдвига.

Система Куэтта.В реометрах данного типа внешний цилиндр вращается двигателем с определенной скоростью, они являются CR реометрами (Рис.4.). Вращение внешнего цилиндра вызывает течение жидкости в зазоре. Крутящий момент, пропорциональный вязкости жидкости, вызванный ее сопротивлением передается на внутренний цилиндр. Его определяют измеряя необходимый противодействующий крутящий момент, прикладываемый для сохранения неподвижного состояния внутреннего цилиндра. На рис.3. в качестве датчика крутящего момента установлен двигатель, обеспечивающий состояние покоя внутреннего цилиндра. Момент измеряется исходя из потребляемой мощности вторым двигателем.

За счет движения наружного цилиндра, течение в приборе с измерительной системой Куэтта, остается ламинарным даже при исследовании низковязких жидкостей при больших скоростях.

CS и CR реометры измерительных систем Куэтта и Серле для идентичных нетиксотропных жидкостей дают одинаковые кривые течения.

Основные закономерности течения вязкой жидкости между двумя коаксиально-цилиндрическими поверхностями бесконечной длины были найдены М. Маргулесом.

R_H — радиус наружной неподвижной измерительной поверхности;

R_В — радиус внутренней вращающейся поверхности (внутренний цилиндр);

ω – угловая скорость вращения внутреннего цилиндра;

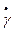– градиент скорости сдвига.

Вследствие прилипания кольцевой слой материала у поверхности внутреннего цилиндра движется с той же угловой скоростью ω. Для элементарного кольцевого слоя материала, расположен­ного на расстоянии r от оси вращения, градиент скорости равен:

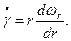(4.3)

Тангенциальная сила на радиусе r по закону Ньютона равна

(4.4)

здесь L — высота рассматриваемого цилиндрического слоя; — вязкость материала.

Сила F_r на радиусе r создает момент, который уравновешивается равным и противоположным по знаку постоянным внешним крутящим моментом М:

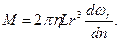(4.5)

Интегрируя уравнение (3), получим

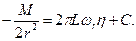
Постоянная интегрирования и момент определяются из граничных условий:

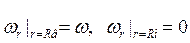
отсюда

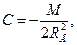
(4.6)

Из формулы (4.6) можно определить вязкость жидкости

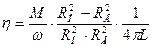(4.7)

или

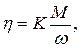(4.8)

где K – коэффициент геометрии прибора, который для данных воспринимающих элементов остается постоянным,

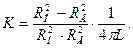(4.9)

Найдем выражение для градиента скорости материала в за­зоре между цилиндрами.

Подставляя (4.6) в (4.4) получим значение скорости сдвига в рабочем зазоре цилиндров:

(4.10)

В коаксиальном цилиндрическом слое радиуса r, приложенный к нему момент уравновешивается моментом, обусловленным дей­ствующим в нем напряжением сдвига τ_r Следовательно:

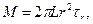
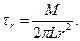(4.11)

Отсюда видно, что градиент скорости и напряжение сдвига в радиальном направлении не являются постоянными величинами.

Наибольшие значения 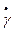и 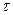имеют на поверхности внутрен­него цилиндра, наименьшее — на поверхности наружного ци­линдра, причем

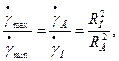
(4.12)

Эти выражения определяют неоднородность полей градиентов скорости и напряжений сдвига в зазоре ротационных вискози­метров. Наличие неоднородности напряженного состояния несу­щественно для обработки результатов вискозиметрических испы­таний в случае материалов, подчиняющихся закону Ньютона, но оно чрезвычайно усложняет обработку вискозиметрических экспериментов, проведенных на приборах с большими зазорами для неньютоновских материалов.

Характеристика вязкостных свойств материалов, которые ве­дут себя как неньютоновские жидкости, определяется видом зави­симости 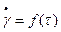. Исследование таких жидкостей, производиться с использованием ротационных вискозиметров с малыми зазорами. За счет малых зазоров между цилиндрами реализуется высокая однородность полей напряжений и градиентов скоростей ( ). Когда однородность напряженного состояния достаточно высока, действующее в материале на­пряжение сдвига принимают равным его среднему значению :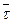

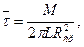(4.13)

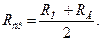(4.14)

Средний градиент скорости находят из соотношения:

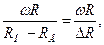(4.15)

где 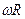- линейная скорость вращающегося цилиндра.

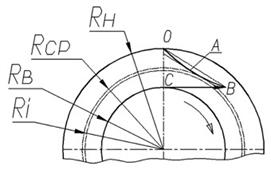
Рис.1. Распределение скоростей при течении жидкости в коаксиально-цилиндрическом вискозиметре.

Смысл выражения (4.15) виден из рассмотрения рисунка. Здесь кривая ОАВ показывает профиль линейных скоростей в зазоре вискозиметра. Средний градиент скорости в этом зазоре численно равен тангенсу угла BOC. Если к профилю скоростей провести секущую OB и затем провести касательную, параллельную этой секущей, то градиент скорости на радиусе R_i будет равен среднему градиенту скорости. Из рисунка видно, что при малых зазорах между цилиндрами замена градиента скорости на радиусе R_i средним градиентом скорости не вносит существенной погрешности вследствие близости R_cp и R_i.