Расчетно-табличный метод минимизации

Расчетный метод минимизации.

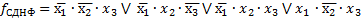
Этап

Выполняются все возможные склеивания членов заданной функции. Эта процедура осуществляется за несколько шагов и в результате каждого из них происходит понижение ранга склеиваемых членов на единицу.

1 шаг) 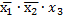и

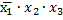
Результат склеивания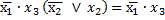

2 шаг) 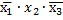и

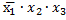
Результат склеивания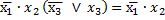

3 шаг) 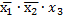и

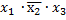
Результат склеивания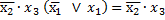

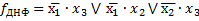
Затем выполняется испытания на склеивание всех членов функции в промежуточной форме .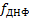

Из соотношения 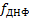видно, что все его члены изолированы друг от друга. Следовательно, полученная промежуточная форма является сокращенной ДНФ исходной СДНФ.

Необходимо убедиться, что все конституенты исходной СДНФ участвовали хотя бы в одном склеивании и в сокращенной форме максимального ранга не будет.

Этап

Выполним проверку каждой простой импликанты в СДНФ, чтобы выявить и удалить лишние члены.

На значение истинности функция влияет только импликанта, которая сама равна 1.

Любая импликанта становится равной 1лишь на одном определенном наборе значений истинности своих аргументов.

Однако, если на этом наборе сумма остальных членов тоже обращается в 1, то рассматриваемая импликанта не влияет на значение истинности функции даже в этом единственном случае, т.е. является лишней.

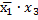1) =1

При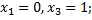

Сумма остальных членов на этом же наборе:

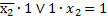
Следовательно проверяемый член лишний.

2)

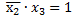
При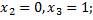

Сумма остальных членов на этом же наборе:

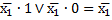
Следовательно проверяемый член не лишний.

3)

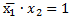
При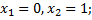

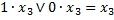
Следовательно проверяемый член не является лишним.

Таким образом, отбросив лишний член, получим тупиковую ДНФ исходной функции

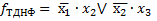
Если лишних членов оказывается больше, например два, то оба отбросить нельзя, т.к. каждый из них проверялся при вхождении другого в оставшуюся сумму. Следовательно, можно отбросить только один из них, а затем снова произвести проверку возможности отбрасывание второго члена.

Этап

Попытаемся упростить ТДНФ.

*Для аппаратурной реализации ТДНФ потребуется восемь условных транзисторов.

Каждому входу любого логического элемента в некотором приближении соответствует один составной КМОП – транзистор (в схемах присутствует дополнительный (выходной) КМОП транзистор, осуществляющий инверсию, но во многих случаях он может и отсутствовать).

Следовательно, любую логическую схему можно оценить по количеству потребного для её реализации оборудования, подсчитав количество входов всех элементов, составляющих эту схему (суммарное число входов всех элементов). Это оценка по Квайну является приближенной, т.к. логические элементы могут строиться на различных принципах и по различным схемам (на многоэмиттерных транзисторах, по схеме токовых переключателей и т.д.). Такая оценка является очень удобной, т.к. объективна, доступна на самых ранних стадиях логического проектирования, главное, все – таки достаточна точна при сравнительных ( а не абсолютных) оценках различных вариантов одного и того же устройства.*

Применим к 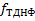распределительный закон второго рода

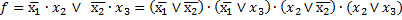
*Распределительный закон второго рода: сумма некоторой логической переменной и произведения нескольких аргументов равно произведению сумм каждого сомножителя и этой переменной.

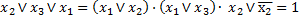
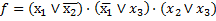
Применим распределительный закон первого рода

*Произведение суммы нескольких аргументов на какую либо (логическую) переменную равно сумме произведений каждого слагаемого на эту переменную

*

=>

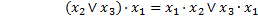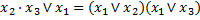
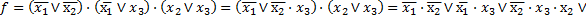
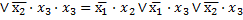
Введём в состав функции нулевой член 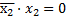и выполним преобразования.

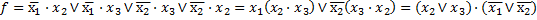
Применим ко второму конъюнктивному члену правило Де Моргана и получим минимальную форму исходной функции.

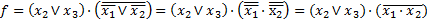
Для аппаратурной реализации потребуется всего семь условных транзисторов.

Расчетно-табличный метод минимизации

Отличается от расчетного только методикой выявления лишних членов в сокращенной ДНФ(КНФ). Этот метод был предложен американским ученым У. Квайном.

Первый и третий этапы будут идентичны соответствующим этапам при расчетном методе.

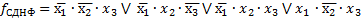
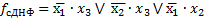
2 Этап

Для выявления возможных лишних членов в сДНФ строится таблица, входными величинами в которой будут конституенты – члены СДНФ и простые импликанты – члены сДНФ.

Поэтому такую таблицу называют конституентно-импликантной матрицей; либо таблицей Квайна, либо таблицей покрытий.

Число строк = числу простых импликалет в сДНФ. Строки делятся на столбцы, число столбцов = числу конституент в СДНФ.

Простые импликанты	Конституенты
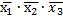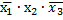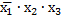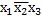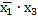	}лишняя	X		X
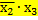	}ядро	X			X
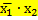		X	X

Процесс минимизации начинается с последовательного сопоставления каждой простой импликанты со всеми конституентами.

Если какая-либо импликанта является собственной частью некоторой конституенты, то в табличной клетке, соответствующей обоим членам, проставляется любой условный значок.

Значки в каждой строке заполненной таблицы показывают, какие члены совершенной формы функции появятся в семействе конституент при развёртывании данной простой импликанты. Т.е. значки показывают, какие конституенты покрываются рассматриваемой импликантой.

В идеальном случае каждая импликанта покрывает только свою конституенту и в каждом столбце находится только один условный значок.

Практически этого не происходит.

Часто одна и та же конституента покрывается в таблице несколькими импликантами.

Необходимо вычеркиванием некоторых (лишних) импликант попытаться оставить в каждой колонке только один значок или минимальное их число.

Вначале по таблице находится ядро функции, состоящее из тех импликант, каждая из которых осуществляет единственное покрытие некоторой конституенты и поэтому никоим образом не может оказаться лишней.

В ядро входят импликанты 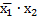и 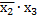. Вычеркивание 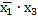не нарушает условия о наличии хотя бы одного покрытия каждой конституенты.