Логическое отрицание (инверсия)

Логическое отрицание (инверсия) образуется из высказывания с
помощью добавления частицы «не» к сказуемому или использовании
оборота речи «неверно, что...». , ;

Примеры образования логического отрицания:

Высказывание Л	Значение	Инверсия	Значение
	высказывания А	высказывания А	инверсии высказывания А
У меня есть		У меня нет
приставка Dendy		приставки Dendy
Я не знаю		Неверно, что я не
китайского		знаю китайского
языка		языка. (Я знаю китайский язык)

,.1.

Поясним эти примеры: ^;' „ , ^!

1) А = У меня есть приставка Dendy — высказывание.

Пусть у вас ее нет, тогда это высказывание ложно {А = 0). Инверсия А —
это высказывание У меня не есть приставка Dendy или высказывание
Неверно, что у меня есть приставка Dendy. Более правильным в русском
языке является предложение У меня нет приставки Dendy, и это выска­
зывание будет истинным. *

2) А =Яне знаю китайского языка — высказывание.

Пусть вы действительно не знаете китайского языка, тогда это выска-; зывание истинно {А = 1). Инверсия А есть высказывание Неверно, что я, не знаю китайского языка, которое является ложным.

логики

Часть 1. Элементы математической

Любую операцию необходимо как-то обозначать.

Обозначение инверсии:НЕ А; —\А\ А', NOT А (В данном пособии: А ■)

Нас интересует истинность высказывания, имеющего форму А (вне зависимости от его содержания). Определяется она по специальной таб-

• ft «Д«'Ч'С

Лице истинности.

;:,',п'ли„1\1 His-

Таблица истинности:

Смысл высказывания А для указанных значений

Значение высказывания: У меня нет приставки _______ Dendy______ Истина

У меня нет приставки Dendy

У меня есть приставка Dendy___

Ложь

Пояснение:

А	_ А
|

Из таблицы истинности следует, что инверсия высказывания истин­на, когда высказывание ложно, и ложна, когда высказывание истинно. Иногда это свойство принимают за определение операции инверсии.

Мнемоническое правило:слово «инверсия» (от лат. inversio — переворачивание) означает, что белое меняется на черное, добро на зло, красивое на безобразное, истина на ложь, ложь на истину, ноль на один, один на ноль.

Операцию инверсии можно графически проиллюстрировать с помо­щью диаграмм Эйлера — Венна.

В теории множеств логическому отрицанию соответствует операция дополнения к множеству.

Примечание.

Близость законов алгебры высказываний к законам алгебры мно­жеств можно продемонстрировать следующим образом. С одной сто­роны, каждое множество может быть описанолибо при помощи пря­мого перечисления его элементов, либо путем указания свойства, ко-

Глава 3. Логические операции

торому должны удовлетворять все элементы данного множества и толь­ко эти элементы. Так, можно говорить о множестве, состоящем из че­тырех студентов: Пети, Гали, Коли, Оли, или о множестве отличников данной студенческой группы, имея в виду в обоих случаях одно и то же множество.

С другой стороны, выбрав какое-то высказывание, можно рассмот­реть множество всевозможных объектов, к которым это высказывание относится, и выделить из него подмножество, для элементов которого это высказывание будет истинным (множество истинности высказывания). Так, множество истинности высказывания Этот студент — отличник для рассмотренной выше студенческой группы будет включать в себя ту же четверку студентов.

Для построения соответствующей дополнению к множеству диаграммы

Эйлера — Венна выберем строку таблицы истинности, в которой А = 1. На диаграмме заштрихуем область, в которой значение А такое же, как в выбранной строке, т. е. 0. Здесь и далее следует учесть: в области, изоб­ражающей объем понятия Л (множество Л), значение А равно 1, вне этой области — 0.

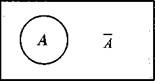
Графическая иллюстрация:_

" ^{! г} I. п

А — множество отличников; . « , !

А — множество неотличников. • ■

i

Т ' i ^: ,"0".."!

...V-.- -•■' '• , -\~. I

Примечания:

1. Логики при образовании инверсии предпочитают иметь дело с обо­ротом речи «неверно, что», поскольку тем самым подчеркивается отри­цание всего высказывания.

2. Дважды или четырежды отрицающееся высказывание имеет то же самое значение истинности, что и исходное высказывание, триж­ды отрицающееся — что и отрицающееся один раз. Например, выс­казывание А = Неверно, что математика — не царица наук имеет то же значение истинности, что и высказывание В = Математика — царица наук.

26

______________________ Часть 1. Элементы математинеокой логики