Основные операции алгебры высказываний
Логическая операция КОНЪЮНКЦИЯ (лат. conjunctio - связываю):
· в естественном языке соответствует союзу и;
· обозначение: &;
· в языках программирования обозначение: and;
· иное название: логическое умножение.
Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Таблица истинности конъюнкции:
| А | В | А&В |
Поскольку таблица истинности для конъюнкции совпадает с таблицей умножения, если истинному высказыванию приписать значение '1', а ложному - '0', то сложное высказывание можно назвать произведением.
Функция конъюнкции истинна тогда, когда истинны одновременно оба высказывания. Читается «А и В». Возможно обозначение «&», «L», «*», «и». Графическое изображение функции представлено на рис. 1.
|

|
 ALB
ALB
 B
B
Рис. 1. Конъюнкция.
Логическая операция ДИЗЪЮНКЦИЯ (лат. disjunctio - различаю):
· в естественном языке соответствует союзу или;
· обозначение: Ú;
· в языках программирования обозначение: or;
· иное название: логическое сложение.
Дизъюнкция - это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда хотя бы одно из двух образующих его высказываний истинно.
Таблица истинности дизъюнкции:
| А | В | АÚВ |
Составное высказывание, образованное в результате дизъюнкции, истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний.
Например.Имеем четыре составных высказывания, образованных с помощью дизъюнкции:
1. «2х2=5 или 3х3=10»
2. «2х2=5 или 3х3=9»
3. «2х2=4 или 3х3=10»
4. «2х2=4 или 3х3=9»
Здесь истинны 2, 3 и 4 высказывания.
Итак, составное высказывание истинно тогда, когда истинно хотя бы одно простое высказывание, входящее в него.
Читается «А или В». Возможно обозначение «v», «+», «или». Графическое изображение функции представлено на рис. 2.
|
 AvB
AvB

 B
B
Рис. 2.Дизъюнкция.
Логическая операция ИНВЕРСИЯ (лат. inversio - переворачиваю):
· в естественном языке соответствует словам "Неверно, что... " и частице не;
· обозначение: не А; 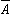 ; ØА
; ØА
· в языках программирования обозначение: not;
· иное название: отрицание.
Отрицание - это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.
Таблицы истинности отрицания:
| А | не А |
| A | F= 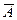 |
Функция логического сложения ИЛИ (ЛогЗнач1;ЛогЗнач2;…) дает значение TRUE (Истина), только тогда, когда хотя бы один логический аргумент имеют значение TRUE (1).
Функция логического отрицания НЕ (ЛогЗнач) дает значение TRUE (Истина), когда логический аргумент имеют значение FALSE (0) и, наоборот, значение FALSE (Ложь), когда логический аргумент имеют значение TRUE (1).
Читается «не А», или «А с чертой», или «отрицание А». Обозначается 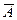 . Графическое изображение функции представлено на рис. 3.
. Графическое изображение функции представлено на рис. 3.
|
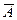
 |  |

Рис. 3.Инверсия.
Логическая операция ИМПЛИКАЦИЯ (лат. implicatio - тесно связываю):
· в естественном языке соответствует обороту Если ..., то ...;
· обозначение: 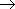 ;
;
· иное название: логическое следование.
Импликация - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.
Таблица истинности импликации:
| А | В | А 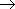 В В |
Логическая операция ЭКВИВАЛЕНЦИЯ (лат. аequivalens - равноценное):
· в естественном языке соответствует оборотам речи тогда и только тогда и в том и только в том случае;
· обозначение: ~ ;
· иное название: равнозначность.
Эквиваленция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
Таблица истинности эквиваленции:
| А | В | А~В |
Все виды логических операций удобно свести в одну таблицу: