Основные методы кодирования
Для оценки возможностей и путей построения эффективных кодов, рассмотрим математическую модель визуальной информации. Будем считать, что значение яркости в каждой точке (х, у) представляется случайной функцией F(x,y) , а отсчет а есть случайная величина, выбранная из конечной генеральной совокупности 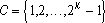 . Можно предложить несколько моделей случайного выбора, отличающихся сложностью описания и степенью соответствия реальным процессам. В простейшей из них положим, что отсчеты независимы и каждый из них принимает i=e значение с вероятностью p(i) , т. е. p(a=ai)=p(ai) , ai
. Можно предложить несколько моделей случайного выбора, отличающихся сложностью описания и степенью соответствия реальным процессам. В простейшей из них положим, что отсчеты независимы и каждый из них принимает i=e значение с вероятностью p(i) , т. е. p(a=ai)=p(ai) , ai 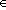 C . В этом случае энтропия hi(a) каждого отсчета а равна
C . В этом случае энтропия hi(a) каждого отсчета а равна
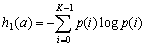 | (5) |
Если сделать еще одно упрощающее предположение и принять, что все значения отсчетов равновероятны, т. е. p(i)=1/K , получим h1=k бит. В этом частном случае в соответствии с теоремой Шеннона [4] не существует способов кодирования, для которых l<k .
Сжатие информации возможно, если принять во внимание неравномерность распределения значений отсчетов и их взаимную зависимость. Оценку сокращения избыточности за счет учета неравномерности распределения дает формула (5), т.е. максимальный коэффициент сокращения (4) равен k/h1 . Как показали исследования телевизионных изображений, избыточность, вносимая не одинаковой вероятностью значений отсчетов, относительно невелика и позволяет сократить объем памяти не более чем в 1,5 раза.
Более существенного сокращения можно достичь, если учесть реально существующую статистическую зависимость между отсчетами. Наиболее просто учесть такую зависимость, описывая последовательность отсчетов цепью Маркова [4]. С этой целью линейно упорядочим отсчеты в соответствии с каким-либо способом сканирования плоскости, например в виде (1). В первом приближении примем во внимание зависимость только между соседними отсчетами. Опишем такую зависимость с помощью условных вероятностей p(i/j) . Здесь p(i/j) - вероятность того, что отсчет имеет значение i при условии, что предыдущий равен 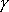 . Тогда условная энтропия h2(a/j) символа цепи Маркова, вычисленная при условии, что предыдущий символ имеет значение j , равна
. Тогда условная энтропия h2(a/j) символа цепи Маркова, вычисленная при условии, что предыдущий символ имеет значение j , равна
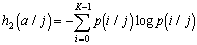
Выражение для безусловной энтропии h2(a) можно получить, усреднив h2(a/j) :
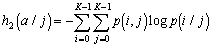 | (6) |
где p(j,i)=p(j)p(i/j) - вероятность события, заключающегося в том, что два соседних символа имеют значения j , i . Формула (6) допускает естественное обобщение, когда модель учитывает статистическую зависимость каждого отсчета от поля изображения A(r-1) , содержащего r-1 отсчетов:
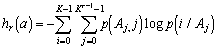 | (7) |
где p(Aj,i) - вероятность события, заключающегося в том, что после r-1 отсчетов, образующих слово Aj , следует отсчет с яркостью i ; p(i/Ai) - условная вероятность того, что после комбинации Ai следует отсчет с яркостью i . Естественно, что h1 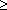 h2
h2 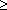 h3 (при r
h3 (при r 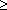 2 ). Причем hr зависит от того, какие r-1 элементов изображения образуют поле A(r-1) . Обычно рассматривают статистическую зависимость между несколькими соседними элементами каждой строки и каждого столбца матрицы отсчетов. Полагая l=hr , можно получить оценку максимально достижимых коэффициентов сокращения для каждой модели визуальной информации.
2 ). Причем hr зависит от того, какие r-1 элементов изображения образуют поле A(r-1) . Обычно рассматривают статистическую зависимость между несколькими соседними элементами каждой строки и каждого столбца матрицы отсчетов. Полагая l=hr , можно получить оценку максимально достижимых коэффициентов сокращения для каждой модели визуальной информации.
Учет статистической зависимости между отсчетами лежит в основе построения первичных способов кодирования визуальной информации. Такие коды интенсивно разрабатывали и исследовали в основном для передачи телевизионных изображений, и соответствующие результаты довольно широко представлены в литературе. Очевидно, что коды, используемые только для передачи и воспроизведения изображений и коды, предназначенные для обработки изображений в ЭВМ, должны удовлетворять различным требованиям. Во-первых, к таким кодам предъявляют разные требования по точности представления изображения. При передаче телевизионных изображений предполагается, что в конце передачи картина будет воспроизведена на экране телевизора и воспринята человеком. Поэтому при создании соответствующих кодов учитывают свойства зрения. Оказывается, что не всегда изображение, субъективно воспринимаемое как хорошее, достаточно точно отображает отдельные детали, необходимые для промышленного зрения. Во-вторых, процессы кодирования и декодирования информации при ее передаче существенно отличаются от процессов хранения и обработки информации в ЭВМ. В результате, коды, допускающие достаточно простую аппаратную реализацию передачи информации, оказываются "неудобными" для представления информации в ЭВМ. Так, коды, используемые в цифровом телевидении, не учитывают особенности словарной структуры памяти ЭВМ, используемые в ЭВМ способы адресации информации и организации массивов и их описаний, возможности многократного считывания отдельных элементов изображения, а также ряд других особенностей программной обработки информации. Несмотря на весомость отличий в требованиях, предъявляемых к кодам, методы кодирования, используемые в цифровом телевидении, при выборе способа представления визуальной информации в ЭВМ заслуживают самого тщательного изучения. Ниже приводится краткий обзор таких методов.
Статистические методы кодирования информации.Статистические коды относятся к неравномерным, т. е. одинаковым по размерам элементам изображения присваиваются кодовые слова неравной длины. Сжатие информации достигается за счет того, что для представления наиболее вероятных значений яркостей выбирают короткие кодовые слова, а для наименее вероятных - длинные.
Относительно просто такой код получается, если принять модель, в которой отсчеты считаются независимыми. Если известно распределение вероятностей p(i) , то для построения эффективных кодов можно воспользоваться методикой Хаффмена или Шеннона - Фано [4]. При этом можно получить хорошее приближение к предельно достижимому коэффициенту сокращения, затрачивая на представление каждого символа в среднем слово длиною h1 бит.
Сложнее строятся коды, в которых учитывается статистическая зависимость между яркостями в соседних точках изображения. В этом случае кодовое слово, сопоставленное определенному значению яркости, изменяется в зависимости от значения яркости в предшествующей точке. Таким образом, способ кодирования каждого i-ro отсчета определяется значением соседнего (i-1)-го отсчета. Построить эффективные коды можно по следующей методике. Перебираются все возможные значения яркости j=0,1,2,...,2k-1 предшествующего элемента и для каждого j строится свой код Хаффмена или Шеннона - Фано, исходя из распределения условных вероятностей p(i/j) . В качестве предшествующего элемента обычно используют соседний отсчет в строке или столбце. Как показали соответствующие исследования телевизионных изображений, на этом пути можно сжать изображение в два-три раза.
Дальнейшее сокращение объема памяти можно получить, если учитывать не один, а одновременно два или три соседних отсчета. Однако при этом существенно усложняется процедура кодирования и декодирования, а выигрыш относительно невелик. Так, учет двух предыдущих элементов (например, соседних по строке и столбцу) позволяет сократить описание, получающееся при учете только одного соседнего элемента, на 20-25%. В связи с этим кодирование триад широкого распространения не получило.
Другой подход к кодированию изображения с учетом предшествующего элемента заключается в представлении разностей соседних отсчетов. Разности кодируются по той же методике Хаффмена и Шеннона - Фано с учетом соответствующей функции распределения вероятностей. Теоретический предел сокращения объема памяти при кодировании разностей как и при кодировании пар отсчетов определяется формулой (6).
Статистические методы кодирования обладают двумя существенными недостатками. Во-первых, статистические свойства зависят от характера представляемого изображения. В связи с этим необходим процесс адаптации, что усложняет использование таких кодов. Во-вторых, статистические коды обладают малой помехоустойчивостью. Искажение одного символа влечет искажение и всех последующих. В связи с этим периодически требуется представлять значение некоторых опорных элементов независимо от значений их соседей.
Кодирование серий.Серией называется последовательность отсчетов, имеющих одинаковое значение. Все изображение можно представить в виде последовательности серий. В полутоновых изображениях серии обычно содержат небольшое число элементов. Поэтому в таких случаях переходят к приближенному описанию, определяя серию как последовательность элементов, значения которых отличаются одно от другого не более чем на  , где (
, где (  - порог, определяющий требуемую точность представления информации).
- порог, определяющий требуемую точность представления информации).
Для представления изображений в виде серий задают либо координаты граничных элементов, либо длины серий. Число символов, требуемое для представления строки в двух рассмотренных способах кодирования, совпадает и равно числу серий. Однако количество разрядов, необходимое для представления длин серий, статистически меньше, чем при задании координат граничных элементов. Таким образом, из двух способов кодирование длинных серий требует меньшего объема памяти, но обладает меньшей помехоустойчивостью, так как ошибка в одном коде искажает всю строку. Под представление длины серии отводят элемент списка. Число разрядов этого элемента выбирают меньшим, чем требуемое для представления максимальной длины, равной числу отсчетов в строке. При этом, если длина серии не представляется одним элементом, серия разбивается на несколько серий максимальной длины. Для того чтобы распознать подобные ситуации, в каждом элементе кодирования выделяется поле под представление признака серии - значения яркости отсчетов, принадлежащих серии. Наиболее удобно кодирование серий используется для представления двухградационных изображений.
Кодирование с предсказанием.Основная идея способа кодирования с предсказанием заключается в том, что каждый отсчет ai можно предсказать на основе анализа нескольких предыдущих отсчетов ai1 , ai2 ,…,air . В результате предсказания получается некоторая оценка 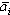 i-го отсчета как функция предыдущих отсчетов
i-го отсчета как функция предыдущих отсчетов
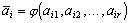 | (8) |
Для представления изображения используются разности между предсказанными и истинными значениями отсчетов
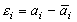 | (9) |
называемые ошибками предсказания. Если известны значения отсчетов в нескольких базовых точках и матрица ошибок предсказания, то по (8) и (9) можно восстановить изображение. Ошибка предсказания задается одним из ранее рассмотренных способов. При правильно выбранной функции предсказания энтропия ошибок существенно меньше энтропии отсчетов, рассматриваемых без учета взаимосвязи, что и позволяет сократить объем памяти для представления изображения.
Как правило, функция предсказания выбирается из класса линейных:
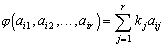
Причем в качестве предшествующих элементов используют обычно не более трех элементов растра. Соответственно различают одно, двух или трехмерные предсказатели. В одномерном предсказателе значение отсчета предсказывается равным предшествующему в строке, в двухмерном - для предсказания используют значения предшествующего элемента той же строки и соответствующего элемента предыдущей строки, в трехмерном (дополнительно к перечисленным двум) - предшествующий элемент предыдущей строки. Для двух и трехмерных предсказателей коэффициенты выбирают по критерию минимальной среднеквадратичной ошибки предсказания. Предсказание основывается на статистической зависимости каждого отсчета от предшествующих. Максимальный коэффициент сокращения  можно оценить по (4) и (7), положив l=hr(a) .Как показали исследования, кодирование с предсказанием позволяет достичь сжатия информации в 3-3,5 раза.
можно оценить по (4) и (7), положив l=hr(a) .Как показали исследования, кодирование с предсказанием позволяет достичь сжатия информации в 3-3,5 раза.
Прочие методы кодирования.В заключение приведем краткое описание некоторых вариантов кодирования, которые интенсивно развиваются для передачи визуальной информации. Здесь следует прежде всего назвать адаптивные методы кодирования. В них в процессе передачи информации так или иначе исследуются статистические свойства сигналов и в соответствии с результатами корректируется способ кодирования. Поскольку все рассмотренные выше коды опираются на статистические свойства изображений, адаптация возможна для каждого из них. Недостаток адаптивных алгоритмов, затрудняющих их применение для представления визуальной информации в ЭВМ, связан с относительной сложностью декодирования информации. Этот недостаток становится весьма существенным, если в процессе обработки информации значение каждого отсчета необходимо считывать и восстанавливать несколько раз. В связи с этим представляется, что процессы адаптации могут эффективно использоваться в системах промышленного зрения для настройки алгоритмов дискретизации видеосигнала с целью компенсации искажений, обусловленных неравномерностью освещенности и другими аналогичными причинами, но не для представления изображений в памяти ЭВМ.
Широко обсуждаются в литературе алгоритмы кодирования изображений, основанные на преобразованиях Фурье, Адамара, Хаара или Карунена - Лоэва [1-4]. При таком кодировании изображение представляется набором полученных в результате преобразования коэффициентов. Кодирование с преобразованием позволяет достичь существенного сжатия информации и хорошего качества передачи телевизионных сигналов. Однако из-за сложности алгоритмов декодирования оно пока находит применение лишь в специальных системах обработки изображений.
Литература.
- Васильев В.И. Распознающие системы. Справочник. - Киев: Наукова думка, 1983. - 422 с.
- Методы передачи изображений. Сокращение избыточности / У.К. Прэтт, Д.Д. Сакрисон, Х.Г. Мусман и др.; Пер. с англ. / Под ред. У.К. Прэтта. - М., Радио и связь, 1983. - 264 с.
- Томашевский Д.И., Масютин Г.Г., Явич А.А., Преснухин В.В.Графические средства автоматизации проэктирования РЭА. - М.: Сов. радио, 1980. - 224 с.
- Бутаков Е.А. и др. Обработка изображений на ЭВМ/ Е.А.Бутаков, В.И. Островский, И.Л. Фадеев. - М.: Радио и связь, 1987. - 240 с.: ил.
Некоторые области практического применения методов обработки изображений и распознавания образов
В данной работе рассматриваются результаты исследований проблем обработки визуальной информации, которые основываются на использовании методов распознавания образов [1-4, 9]. Современное развитие технологий автоматической обработки визуальной информации позволяет применять их в системах технического зрения при выполнении широкого ряда производственных операций, контроля продукции и др.
На этапе исследований методов распознавания объектов на изображении целесообразно использовать систему MATLAB. С помощью функций BWLABEL, IMFEATURE и др. производится поиск и вычисление признаков объектов.
