Проектирование продольного профиля

Горные дороги отличаются извилистостью трассы, т.е. наличия большого количества кривых в плане вызванных обходом препятствий, пересечением водотоков и развитием трассы. Продольные уклоны горных дорог близки к предельным, принимаем для уменьшения земляные работы. Установление расчетной скорости для назначения продольного уклона производится с учетом интенсивности движения, а также состава движения. Особенно это важно для горных дорог, трассы которых прокладываются с искусственным увеличение длины трассы.

При движении по участкам значительного протяжения с большим продольным уклоном, происходит перераспределение нагрузки между осями автомобиля, в следствии чего шины колес автомобиля преждевременно изнашиваются. Поэтому на трудных участках дорог допускаются затяжные уклоны более 60‰ с обязательным включением участков с меньшими продольными уклонами 20‰ и менее и площадок для остановки автомобилей с расстояниями между ними не более длины участков, указанных в СНиПе.

Проектирование плана и продольного профиля дорог производим из условия наименьшего ограничения и изменения скорости, обеспечения безопасности и удобства движения, возможной реконструкции дороги за пределами перспективного периода.

Для дороги III категории руководствуясь СНиП 2.05.02.85 в качестве основных параметров принимаем:

продольные уклоны - не более 80 ‰;

радиусы кривых в плане - не менее 100 м;

радиусы кривых в продольном профиле:

выпуклых - не менее 1500 м;

вогнутых - не менее 400 м.

Проектирование продольной оси дороги начинается с высоты ПК62+00 с учетом снегонезаносимой насыпи, которая рассчитывается по формуле:

h_сн= h_s+Δh+Δh_о ,м (2.1)

где h_s – высота снежного покрова 5%-й вероятности;

Δh – возвышение бровки насыпи над расчетным уровнем снегового покрова необходимого для ее незаносимости;

Δh_о – превышение оси над бровкой.

h_s для Советского района 0,69 м.

Δh = 0,4 м – в соответствии со СНиП 2.05.02 – 85 (по категории автомобильной дороги, для III категории – согласно задания). [1]

Δh – рассчитывается по поперечному профилю земляного полотна по рисунку 2:

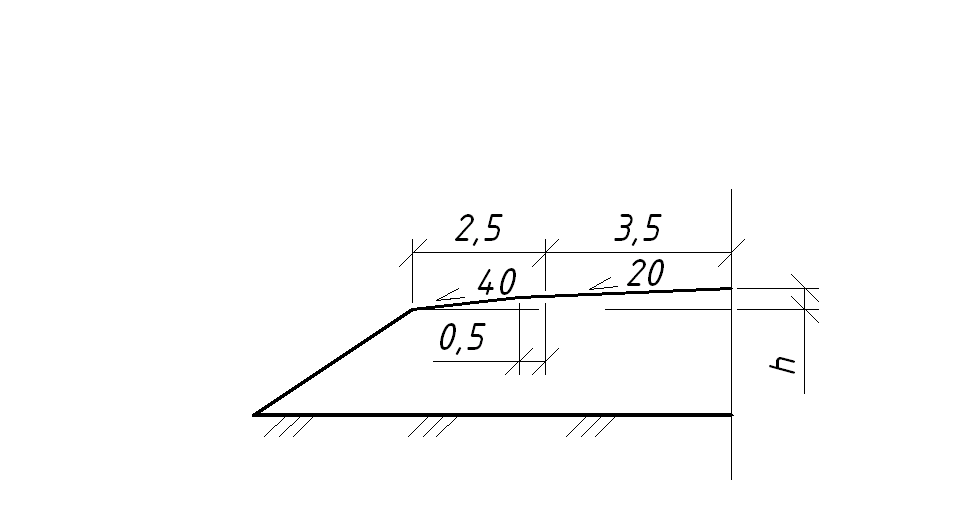
Рисунок 2.2 - Поперечный профиль

Δh₀ = (3,5+0,5)·0,02 + (2,0·0,04) = 0,16 м.

Получаем, что высота снегонезаносимой насыпи по формуле 2.1:

h_сн = 0,4 + 0,60 + 0,16 = 0,8 м

При проектировании автомобильных дорог используются отрезки вертикальных кривых, ограниченных прямыми-касательными с малыми продольными уклонами, что позволяет при расчетах сопряжений горизонтальную проекцию любого элемента проектной линии приравнять длине самого элемента, как это принято в дорожном проектировании.

Координаты параболических кривых при расположении начала координат в вершине кривой связаны уравнением

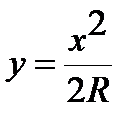(2.2)

Принимая во внимание принятое в дорожном проектировании допущение о равенстве длины элемента профиля его горизонтальной проекции, получаем окончательное уравнение кривой

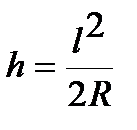(2.3)

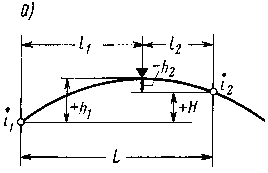
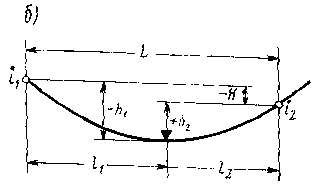
Рисунок 2.3 – Расчетные схемы параболических кривых:а — выпуклая кривая; б — вогнутая кривая

Находя первую производную, получаем

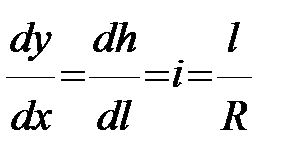
Следовательно, величина уклона в любой точке кривой прямо пропорци­ональна расстоянию l точки от вершины кривой и обратно пропорциональна радиусу кривизны параболы. Находя вторую производную

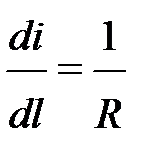или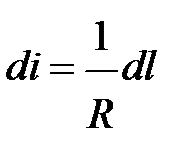

устанавливаем, что уклон векторных точек параболических кривых изменяется равномерно, по прямолинейному закону. Величины уклонов последовательного ряда векторных точек кривой, расположенных на расстоянии 1 м друг от друга, последовательно изменяются в каждом случае на постоянную величину кривизны .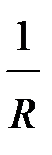

Из приведенных выше формул получаем зависимости, широко исполь-зуемые для вывода формул сопряжения элементов проектной линии (рисунок 2.3).

Расстояние между двумя любыми точками параболической кривой с уклонами i₂ и i₁ равно произведению разности уклонов второй (правой) и первой (левой) точек на радиус

L=( i₂- i₁)R (2.4)

В этой и последующих формулах принято следующее правило знаков: радиусы вогнутых кривых — положительны, выпуклых — отрицательны; уклоны подъёмов — положительны, спусков — отрицательны; превышения —положительны, если последующая точка выше предыдущей, и отрицательны в обратном случае. Такое же правило знаков превышений следует соблюдать при определении их по таблицам. Последовательность точек принята слева направо.

Следовательно, расстояние от точки с уклоном i₂, расположенной справа от вершины, до вершины кривой

l₂=(i₂-0)R=i₂×R (2.5)

расстояние от вершины кривой до точки с уклоном i₂, расположенной слева от вершины,

l₁=(0-i₁)R= - l₁×R (2.6)

превышение второй (правой) точки с уклоном i₂ над первой (левой) точкой с уклоном i₁ равно половине произведения разности квадратов уклонов правой и левой точек на радиус

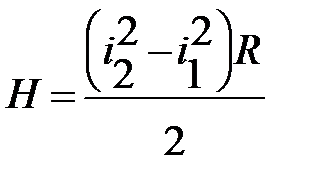(2.7)

Следовательно, превышение точки с уклоном i₂ над вершиной кривой

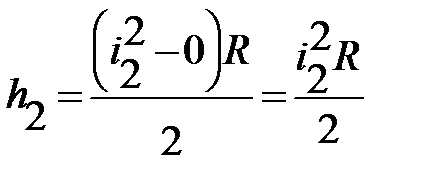(2.8)

или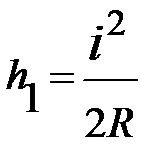

превышение вершины кривой над точкой с уклоном i₁

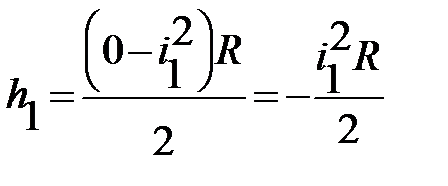(2.9)

или .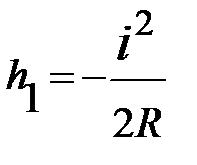

Уклон последующей векторной точки параболы i₂ отличается от уклона i₁ предыдущей векторной точки на величину 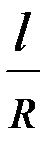, т.е.

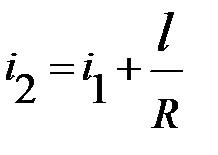, (2.10)

где l – расстояние между точками с уклонами i₂ и i₁ .

( Под уклоном кривой в данной точке подразумевается уклон касательной или уклон этой векторной точки.) [5]

Проектирование продольной оси трассы начинаем с того, что откладываем высоту снегонезаносимой насыпи на ПК 60+00. Шаблон выгнутой кривой R=5000 и проводим линию с уклоном от 50 ⁰/₀₀ до 0 ⁰/₀₀ ПК 60+00 до ПК 62+00. Затем прикладываем шаблон выгнутой кривой радиусом 1500, ориентируем его и проводим кривую от 0 ⁰/₀₀ до 8 ⁰/₀₀ ПК 62+00 до ПК63+20. Берём шаблон вогнутой кривой радиусом 2500, ориентируем его и проводим кривую от 80 ⁰/₀₀ до 0 ⁰/₀₀ с ПК 63+20 до ПК 65+20. Затем прикладываем шаблон выгнутой кривой радиусом 5000, ориентируем его и проводим кривую от 0 ⁰/₀₀ до 30 ⁰/₀₀ ПК 65+20 до ПК66+70. Затем проводим прямую линию с уклоном 30 ⁰/₀₀ с ПК 66+70 до ПК 69+30. Затем прикладываем шаблон выгнутой кривой радиусом 5000, ориентируем его и проводим кривую от 30 ⁰/₀₀ до 80 ⁰/₀₀ ПК 69+30 до ПК72+40. На прямых участках оси трассы отметки получаем, умножая соответствующий уклон на расстояние. По таблицам [5] ищем превышение нуля первой кривой.

Затем по таблицам находим отметки на каждом пикете, по расстоянию от пикета до вершины кривой, берём превышение и отнимаем это превышение от отметки вершины кривой. Если кривая вогнутая, то превышение нужно прибавлять к отметке вершины кривой. Аналогичные действия проводим для других кривых. Получаем следующие отметки оси дороги:

Н_{пк 60}=375,75 м;

Н_{пк 61}=379,50 м;

Н_{пк 62}=380,75 м;

Н_{пк 63}=377,42 м;

Н_{пк 64}=371,08 м;

Н_{пк 65}=368,07 м;

Н_{пк 66}=367,39 м.

Н_{пк 67}=364,88 м;

Н_{пк 68}=361,88 м;

Н_{пк 69}=358,88 м;

Н_{пк 70}=355,46 м;

Н_{пк 71}=350,16 м;

Н_{пк 72}=342,86 м;

Н_{пк 72+40}=337,57 м;

По известным проектным отметкам (красным) и отметкам земли (чёрным) вычисляем рабочие отметки, используя следующую формулу:

r = h_ПР – h_З (2.11)

где h_ПР – проектная отметка;

h_З – отметка земли;

r – рабочая отметка.

Вычисляем рабочее отметки и наносим их на проектную линию. Если рабочая отметка отрицательная, то её отображают ниже проектной линии (она обозначает выемку), а если положительная, то выше проектной линии (она обозначает насыпь).

Получаем следующие рабочие отметки:

r_{пк 60}=0,80 м;

r_{пк 61}=1,56 м;

r_{пк 62}=0,73 м;

r_{пк 63}=3,11 м;

r_{пк 64}=2,08 м;

r_{пк 65}=4,41 м;

r_{пк 66}=1,54 м;

r_{пк 67}=1,41 м;

r_{пк 68}=1,34 м;

r_{пк 69}=0,30 м;

r_{пк 70}=2,16 м;

r_{пк 71}=6,09 м;

r_{пк 72}=2,19 м;

r_{пк 72+40}=3,50

Далее по рабочим отметкам подбираем поперечные профили земляного полотна. Продольный профиль отображен на листе №1 графической части.