Синтез конечных автоматов мура
5.2.1. Абстрактный синтез автомата Мура
Для синтеза схемы конечного автомата Мура необходимо иметь таблицу соответствия, которая получается на основе словесной формулировки работы синтезируемого автомата.
Пример 5. . Получена следующая таблица соответствия: U0U1U2U0U1U2U3U0 – V0V1V2V0V2V1V1V0. Аналогично, как и при синтезе автомата Мили, каждому переходу таблицы соответствия присваивается внутреннее состояние и получается таблица 5.21.
Таблица 5.21.
Таблица соответствия
| U0 | – | а0 | – | V0 |
| U1 | – | а1 | – | V1 |
| U2 | – | а2 | – | V2 |
| U0 | – | а3 | – | V0 |
| U1 | – | а4 | – | V2 |
| U2 | – | а5 | – | V1 |
| U3 | – | а6 | – | V1 |
| U0 | – | а7 | – | V0 |
Для синтеза схемы автомата Мура строится отмеченная таблица переходов. Отмеченная таблица переходов отличается от совмещенной таблицы переходов и выходов автомата Мили тем, что выходами автомата отмечаются все столбцы таблицы переходов. В клетках этой таблицы ставятся только внутренние состояния автомата, число строк и столбцов будет таким же, как и в совмещенной таблице переходов и выходов автомата Мили.
Таблица 5.22.
Отмеченная таблица переходов
| V0 | V1 | V2 | V0 | V2 | V1 | V1 | V0 | |
| а0 | а1 | а2 | а3 | а4 | а5 | а6 | а7 | |
| U0 | а0 | а3 | а3 | а7 | а7 | |||
| U1 | а1 | а1 | а4 | а4 | ||||
| U2 | а2 | а2 | а5 | а5 | ||||
| U3 | а6 | а6 |
Для минимизации отмеченной таблицы переходов (для объединения столбцов) существуют два условия:
- необходимое условие заключается в том, что внутренние состояния, которыми обозначены столбцы, могут объединяться между собой, если они отмечены одинаковыми выходами;
- достаточное условие позволяет объединять столбцы только в том случае, если после переобозначения внутренних состояний в объединяемых клетках будут находиться одинаковые внутренние состояния, или одна клетка заполнена, а другая пустая, или обе клетки пустые.
При минимизации отмеченной таблицы переходов все символы внутренних состояний развиваются на R группы, количество которых равно числу попарно различимых выходных символов. В каждую группу вносятся только те символы внутренних состояний аi, которые отмечены одинаковыми выходными символами Vj. В отмеченной таблице переходов 5.22 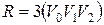 . Переобозначив внутренние состояния символом g по необходимому условию получаем
. Переобозначив внутренние состояния символом g по необходимому условию получаем
х0 – а0а3а7, отмеченные выходом V0
х1 – а1а5а6, отмеченные выходом V1
х2 – а2а4, отмеченные выходом V2
После переобозначения внутренних состояний строится таблица 5.23 для проверки выполнения достаточного условия.
Таблица 5.23.
Отмеченная таблица переходов
| V0 | V1 | V2 | V0 | V2 | V1 | V1 | V0 | |
| а0 | а1 | а2 | а3 | а4 | а5 | а6 | а7 | |
| g0 | g1 | g2 | g0 | g2 | g1 | g1 | g0 | |
| U0 | g0 | g0 | g0 | g0 | g0 | |||
| U1 | g1 | g1 | g2 | g2 | ||||
| U2 | g2 | g2 | g1 | g1 | ||||
| U3 | g1 | g1 |
В полученной таблице 5.23 проверяется выполнение достаточного условия. В строке U1 ранее намеченные к объединению столбцы а0 и а3 по достаточному условию не объединяются в клетке столбца а0 и строки U1 стоит внутреннее состояние х1, а клетке строки U1 и столбца а3 внутреннее состояние х2.
По аналогичным причинам не объединяются столбцы а1а5 и а2а4, поэтому необходимо произвести новое переобозначение внутренних состояний
g0 – а0а7
g1 – а1
g2 – а5а6
g3 – а2
g4 – а4
g5 – а3
Для проверки выполнения достаточного условия строится таблица 5.24. Из таблицы 5.24 следует, что достаточные условия выполняются. Минимальная таблица переходов автомата Мура представлена таблицей 5.25.
Таблица 5.24.
Отмеченная таблица переходов
| V0 | V1 | V2 | V0 | V2 | V1 | V1 | V0 | |
| а0 | а1 | а2 | а3 | а4 | а5 | а6 | а7 | |
| g0 | g1 | g3 | g5 | g4 | g2 | g2 | g0 | |
| U0 | g0 | g5 | g5 | g0 | g0 | |||
| U1 | g1 | g1 | g4 | g4 | ||||
| U2 | g3 | g3 | g2 | g2 | ||||
| U3 | g2 | g2 |
Таблица 5.25.
Минимальная таблица автомата Мура
| V0 | V1 | V2 | V0 | V2 | V1 | |
| g0 | g1 | g3 | g5 | g4 | g2 | |
| U0 | g0 | g5 | g5 | g0 | ||
| U1 | g1 | g1 | g4 | g4 | ||
| U2 | g3 | g3 | g2 | g2 | ||
| U3 | g2 |
5.2.2. Структурный синтез автоматов Мура
Кодирование входов, выходов и внутренних состояний осуществляется так же, как и для автоматов Мили
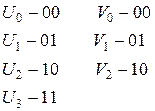
Для кодирования внутренних состояний необходимо построить граф автомата (рис. 5.9).

Рис. 5.9. Граф автомата Мура
После кодирования входов, выходов и внутренних состояний строится структурная таблица переходов автомата Мура.
Таблица 5.26.
Структурная таблица переходов
| у1у2 | ||||||
| Q1Q2Q3 х1х2 | ||||||
Из структурной таблицы 5.26 следует, что синтезируемый автомат Мура имеет два входа х1х2, два выхода у1у2 и три элемента памяти Q1Q2Q3.
Уравнения выходов получаются непосредственно из структурной таблицы переходов следующим образом. Из столбцов где у1 равен единице в уравнение у1 в качестве слагаемых берутся коды внутренних состояний, которыми обозначены столбцы таблицы переходов. Аналогично записывается уравнение для у2
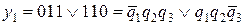
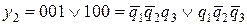 .
.
Как видно из уравнений выходы у1у2 автомата Мура формируются только элементами памяти, а выходы автомата Мили формируются как элементами памяти, так и входами х1х…
Для получения уравнений возбуждения элементов памяти необходимо выбрать элементы автоматики и телемеханики, которые будут использоваться в качестве элементов памяти в автомате Мура.
Если в качестве элементов памяти будет использоваться реле, то таблица переходов автомата Мура 5.26 одновременно будет и таблицей возбуждения.
Для получения минимальных уравнений возбуждения элементов памяти необходимо таблицу 5.26 преобразовать к виду таблицы минимизации на пять переменных. Для этого надо последние две строки поменять местами и добавить два столбца с недостающими кодами 010 и 101.
Таблица 5.27.
Преобразовательная таблица переходов
| q1q2q3 х1х2 | ||||||||
Получение уравнения возбуждения элемента памяти Q1
Таблица 5.28.
Таблица минимизации
 011 011 | ||||||||
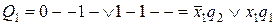 .
.
Аналогично получаются уравнения возбуждения элементов памяти Q2 и Q3.
Таблица 5.29.
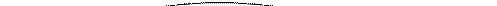 000 000 | ||||||||
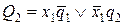 .
.
Таблица 5.30.
 | ||||||||
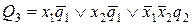 .
.
Схема электрическая функциональная автомата Мура на релейно-контактных элементах показана на рисунке 5.1.

Рис. 5.10. Схема электрическая функциональная автомата Мура
