Нормальное распределение. Наибольшее распространение получил нормальный закон распределения, называемый часто распределением Гаусса:

Наибольшее распространение получил нормальный закон распределения, называемый часто распределением Гаусса:

(**),

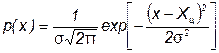где 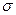– параметр рассеивания распределения, равный СКО; X_ц – центр распределения, равный МО.

Широкое использование нормального распределения на практике объясняется центральной предельной теоремой теории вероятностей, утверждающей, что распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдений формируются под действием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.

При введении новой переменной 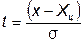из формулы (**) получается нормированное нормальное распределение.

Его интегральная и дифференциальная функции которого соответственно равны:

.

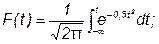
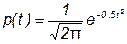Нормирование приводит к переносу начала координат в центр распределения и выражению абсциссы в долях СКО. Значения интегральной и дифференциальной функций нормированного нормального распределения сведены в таблицы, которые можно найти в литературе по теории вероятностей.

Определенный интеграл с переменным верхним пределом

(***)

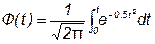называют функцией Лапласа. Для нее справедливы следующие равенства: Ф(-∞) = -0,5; Ф(0) = 0; Ф(+∞) = 0,5; Ф(t) = -Ф(t). Функция Лапласа используется для определения значений интегральных функций нормальных распределений. Функция F(t) связана с функцией Лапласа формулой F(t) = 0,5+Ф(t). Интеграл в формуле(***) не выражается через элементарные функции.