Построение формализованного исчисления высказываний
Способ построения научной теории в виде системы аксиом и правил вывода, позволяющих формальным логическим путем получать утверждения (теоремы) данной теории, называется аксиоматическим методом. Аксиомы (утверждения, принимаемые без доказательств) выделяются, а правила вывода определяются так, что по ним из аксиом могут быть получены все тавтологии алгебры высказываний и только они.
В качестве аксиом выбраны формулы следующих видов:
(A1)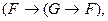 
(А2)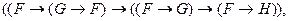 
(А3)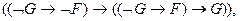 
где F, G, H – произвольные формулы. Таким образом, каждое из выражений (A1), (A2), (A3) задает лишь форму аксиомы. Они превращаются в аксиомы, если вместо F, G, H подставить конкретные формулы (в частности, пропозициональные переменные). Следовательно, каждое из этих выражений задает бесконечное множество формул. Все они называются аксиомами. Поэтому каждое из выражений (A1), (A2), (A3) называют схемой аксиом. Далее определяется следующее правило получения новых формул из имеющихся. Если имеются формулы F и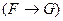 
, то они дают формулу G. Это правило называется modus ponens или правилом отделения (сокращенно m. p.) и записывается так:
.
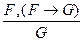Доказательством или выводом формулы F из множества формул (гипотез) Г называется такая конечная последовательность B1, B2 …Bs формул, каждая формула которой является либо аксиомой, либо формулой из Г (гипотезой), либо получена из двух предыдущих по правилу m. p., а последняя формула Bs совпадает с F. Если имеется вывод формулы F из множества гипотез Г, то говорят, что F выводима из Г, и пишут Г ⊢ F.Если же имеется вывод F из пустого множества гипотез, то говорят, что F выводима из аксиом или что F доказуема. В таком случае F называют теоремой и пишут ⊢ F. Если Г = {F1,F2…Fm} ⊢ G, можно писать F1,F2…Fm⊢ G.
Поскольку в аксиомах не участвуют связки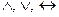 
, то они вводятся с помощью следующих определений: 
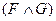обозначает 
; 
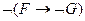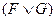обозначает 
; 
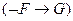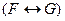обозначает 
.
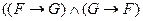Вывод формулы представляет собой последовательность формул, сопровождаемых указаниями, является ли данная формула гипотезой, аксиомой или получена из других формул по некоторому правилу вывода. Принято вначале выписать все гипотезы и слева указывать номер шага вывода.
Пример 3.1.
Построить вывод формулы A⊢ B ®A.
(1) A – гипотеза;
(2) A ® (B ® A) – аксиома (А1);
(3) 
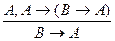– из (1) и (2) по m. p.
Любую равносильную формулу можно рассматривать как правило вывода. Например, закон де Моргана может быть представлен как следующее правило вывода: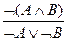 
. Равносильность A ® B º ØB ® ØA порождает закон контрапозиции: 
.
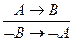Некоторые правила вывода исчисления высказываний.
1. Введение конъюнкции: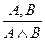 
.
2. Удаление конъюнкции: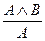 
и 
.
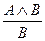3. Отрицание конъюнкции: .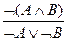
4. Введение дизъюнкци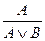и: 
и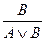 
.
5. Удаление дизъюнкци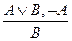и: 
и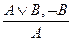 
.
6. Отрицание дизъюнкции: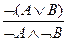 
.
7. Введение импликации: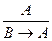 
.
8. Удаление импликации: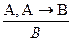 
(m. p.) и 
.
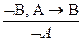9. Отрицание импликации: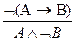 
.
10. Введение эквивалентности: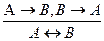 
.
11. Удаление эквивалентност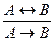и: 
и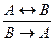 
.
12. Введение отрицания: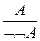 
.
13. Удаление отрицания: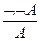 
.
14. Закон контрапозиции: .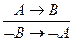
Для построения выводов в исчислении высказываний служит теорема о дедукции:пусть Г – множество формул, A и B – формулы и имеет место вывод: Г, A ⊢ B. Тогда имеет место следующий вывод: Г ⊢ A ® B.
Таким образом, если нужно вывести формулу вида A ®B из множества формул (возможно, пустого), можно ввести дополнительное допущение A.
Важным следствием теоремы дедукции является правило силлогизма:
A ®B, B ® C ⊢ A®C.
Рассмотрим примеры построения вывода в исчислении высказываний.
Пример 3.2.
Обосновать вывод A ® (B ® C), AÙB ⊢ C.
(1) A ® (B ® C) – гипотеза;
(2) AÙB – гипотеза;
(3) A – из (2) и правила удаления конъюнкции;
(4) B ® C – из (1), (3) и m. p.
(5) B – из (2) и правила удаления конъюнкции;
(6) C – из (4), (5) и m. p.
Пример 3.3.
Обосновать правильность следующего рассуждения, построив вывод.
Если число целое, то оно рациональное. Если число рациональное, то оно действительное. Число целое. Значит, оно действительное.
Сначала формализуем наше рассуждение, введя следующие высказывания:
A = “число целое”.
B = “число рациональное”.
C = “число действительное”.
Нужно построить следующий вывод: A ® B, B ® C, A ⊢ C.
Построим этот вывод.
(1) A ® B – гипотеза;
(2) B ® C – гипотеза;
(3) A – гипотеза;
(4) A ® C – из (1) и (2) по правилу силлогизма;
(5) C – из (3) и (4) по m. p.