Синтез вычитающего счетчика

В вычитающем счетчике номер последующего состояния должен быть на единицу меньше предыдущего состояния. Поэтому для вычитающего счетчика 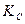=8 таблица функционирования будет иметь вид табл. 4.

Таблица 4

Состояние счётчика	Функция перехода
№	Предыдущее	Последующее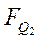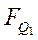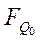
									▼
								▼	▲
									▼
							▼	▲	▲
									▼
								▼	▲
									▼
							▲	▲	▲

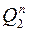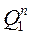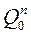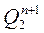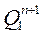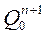На основании таблицы функционирования счетчика составляем для каждого триггера таблицу функций перехода 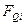для каждого из восьми состояний, значения 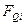заносим в таблицу 4. На основании таблицы переходов триггеров составляем карты функций переходов 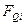для каждого триггера 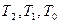(рис, 10).

Рис.10

Рис.11

Заменяя функции переходов в картах рис. 10 значениями функций управления и из словаря переходов (см. табл. 2), получаем карты Карно для входов J и K каждого триггера счетчика (см. рис. 11).

После минимизации получаем логические уравнения входов J и K триггеров счетчика:

, , (4)

Из выражения (4) следует, что на J и K входы второго триггера следует подать конъюнкцию логических переменных с инверсных выходов первого и нулевого триггеров. Входы первого триггера должны быть соединены с инверсным выходом нулевого триггера, а на J и K входы нулевого триггера необходимо подать потенциал, соответствующий логической единице. Схема вычитающего счетчика, построенного в соответствии с полученными результатами, приведена на рис. 12.

Рис.12

Реверсивный счетчик

Реверсивный счетчик осуществляет счет сигналов, как в режиме сложения, так и в режиме вычитания. Режим работы изменяют с помощью схемы управления. В качестве примера рассмотрим синтез восьмиразрядного реверсивного счетчика. Воспользуемся результатами, полученными при синтезе суммирующего и вычитающего счетчиков в пп. 2.2.2. и 2.2.3.

Для этих счетчиков:

I) в режиме сложения ; ;

2) в режиме вычитания ; ; .

Из этих выражений следует, что при изменении режима счета функции на управляющих J и K изменяются на инверсные только на входах второго и первого триггеров. Поэтому для реверсивного счета необходимо произвести коммутацию выходов нулевого и первого триггеров счетчиков. Коммутация осуществляется с помощью сигнала управления Т, применяющего значения 1 при суммировании и 0 при вычитании. Тогда логические уравнения, описывающие схему управления, имеют вид:

Здесь при Т=1 обеспечивается режим сложения, а при Т=0 - режим вычитания. Эти выражения можно преобразовать с помощью логических элемен­тов И-ИЛИ-НЕ [3, с. 232] к виду:

Схема управления, обеспечивающая изменение режима работы счетчика, приведена на рис. 13.

Рис.13