Нахождение линейной функции методом наименьших квадратов

В качестве примера рассмотрим более подробно линейную функцию преобразования вида:

,

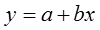где a и b - неизвестные параметры.

Применяя метод максимального правдоподобия, получим систему уравнений, которую разделим на “n” .

.

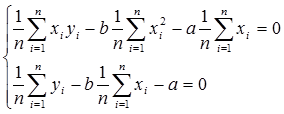Можно получить эту систему другим путем. Минимизируем выражение

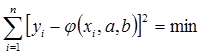
Для нашего случая оно имеет вид:

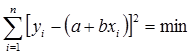
Берем частные производные, приравниваем их к нулю и приходим к той же системе уравнений.

Решая полученную систему уравнений, находим следующие выражения для коэффициентов:

,

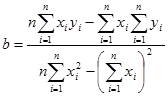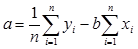
Таким образом, достаточно легко находим линейную зависимость между измеренными величинами.

Особенности применения линейной функции. Линейная функция имеет широкое применение в различных областях науки и техники, поэтому её параметры, а также входящие величины для их вычисления, имеют специальные названия.

Нетрудно видеть, что входящие в данную систему уравнений коэффициенты при неизвестных параметрах представляют собой статистические моменты:

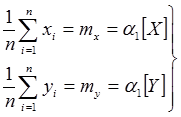- начальные моменты первого порядка;

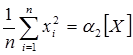- второй начальный момент;

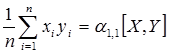- смешанный начальный момент.

Подставляя, получим:

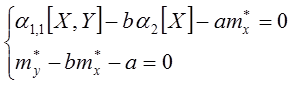
Откуда:

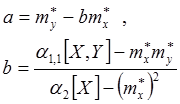
Если ввести статистический корреляционный момент в виде:

,

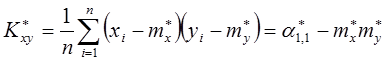а также статистическую дисперсию

,

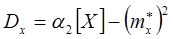тогда получим:

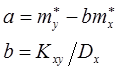
Подставляя полученные значения в функцию преобразования, имеем:

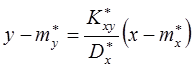
Вводя выражение абсолютной погрешности, можно установить, насколько сходятся теоретические и экспериментальные зависимости:

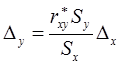
Примечание: Метод наименьших квадратов позволяет решать и находить уравнения и более высоких степеней “k”, однако решение становится более громоздким с возрастанием степени многочлена.

Вопросы к разделу

1. Что такое грубые погрешности и промахи?

2. Как определить присутствие грубых погрешностей и промахов в выборке по виду закона распределения или гистограмме?

3. Расскажите о критерии "трех сигм" и его модификациях.

4. Как применить критерий Романовского для исключения из выборки промахов?

5. В чем суть критерия Шарлье?

6. Расскажите об использовании вариационного критерия Диксона для нахождения промахов.

7. Напишите алгоритм обработки результатов однократных измерений с точным оцениванием погрешностей.

8. Как обрабатываются результаты линейных косвенных измерений?

9. Расшифруйте понятия коррелированных и некоррелированных случайных величин. Что считается границей между этими случайными величинами при их суммировании?

10. Каким образом суммируются коррелированные случайные величины?

11. По каким правилам суммируются некоррелированные случайные величины?

12. Как суммируются случайные и систематические погрешности? Какой нормативный документ регламентирует эти правила?

13. В чем состоит суть критерия ничтожно малой погрешности?