Циркуля-измерителя и линейного масштаба;

Масштабы

Горизонтальные проекции отрезков при составлении карт и планов изображают на бумаге в уменьшенном виде, т.е. в масштабе.

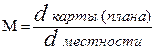Масштаб карты (плана) – отношение длины линии на карте (плане) к длине горизонтальной проекции линии местности:

Масштабы бывают численные и графические.

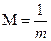Численные

1)В виде простой дроби:

где m – степень уменьшения или знаменатель численного масштаба.

2)В виде именованного соотношения,

например: в 1 см 20 м, в 1см 10 м

При помощи масштабов можно решать следующие задачи.

1. По длине отрезка на плане заданного масштаба определить длину линии на местности.

2. По длине горизонтальной проекции линии определить длину соответствующего отрезка на плане масштаба .

Для того чтобы избежать вычислений и ускорить работу, а также повысить точность измерений на картах и планах, пользуются графическими масштабами: линейным и поперечным.

Линейный масштаб – графическое изображение численного масштаба в виде прямой линии.

Для построения линейного масштаба на прямой линии откладывают ряд отрезков одинаковой длины. Исходный отрезок называется основанием масштаба (О.М.). Основание масштаба - это условно принятая длина отрезков откладываемых по линейному масштабу от нуля в правой части линейного масштаба и одного деление в левой части, которое в свою очередь делится на десять равных частей.

М = 1:10000 Линейный масштаб позволяет оценить отрезок с точностью в 0,1 доли основания точно и до 0,01 доли основания на глаз (для данного масштаба).

Для более точных измерений пользуются поперечным масштабом, имеющем на линейном масштабе дополнительное построение по вертикали.

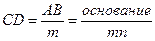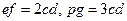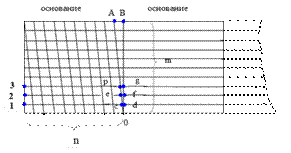
Поперечный масштаб

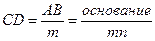После откладывания необходимого количества оснований масштаба (обычно длиною 2 см, и тогда масштаб называется нормальным) восстанавливают перпендикуляры к исходной линии и делят их на равные отрезки (на m частей). Если основание разделено на n равных частей и точки деления верхнего и нижнего основания соединены наклонными линиями так, как показано на рисунке, то отрезок

Поперечный масштаб позволяет оценить отрезок точно в 0,01 доли основания, и до 0,001 доли основания – на глаз.

Поперечный масштаб гравируют на металлических линейках, которые называются масштабными. Перед применением масштабной линейки следует оценить основание и его доли по следующей схеме.

Пример: Пусть численный масштаб 1:5000, именованное соотношение будет: в 1 см 50 м. Если поперечный масштаб нормальный (основание 2 см), то:

• одно целое основание масштаба (о.м.) – 100 м;

• 0,1 основания масштаба – 10 м;

• 0,01 основания масштаба – 1 м;

• 0,001 основания масштаба – 0,1 м

Точность масштаба даёт возможность определить, какие предметы местности можно изобразить на плане, а какие нет из-за их маленьких размеров. Решается и обратный вопрос: в каком масштабе надо составить план, чтобы предметы, имеющие, например, размеры 5 м, были изображены на плане. Для того чтобы в конкретном случае можно было принять определённое решение, вводится понятие точности масштаба. При этом исходят из физиологических возможностей человеческого глаза. Принято, что измерить расстояние, пользуясь циркулем и масштабной линейкой, точнее, чем 0,1 мм, в данном масштабе невозможно (таков диаметр кружка от остро отточенной иглы). Поэтому под предельной точностью масштаба понимают длину отрезка на местности, соответствующую 0,1 мм на плане данного масштаба.

Линейные измерения на топографических картах и планах

Отрезки, длину которых определяют по карте или плану, могут быть прямолинейными и криволинейными.

Определить линейные размеры объекта на карте или плане возможно с помощью:

1. линейки и численного масштаба;

Измеряя отрезок линейкой получим, например, 9,8 см, масштаб 1:10000 или в масштабе –980 м. Оценивая точность линейных измерений следует учесть, что линейкой можно измерить отрезок длиной не менее 0,5 мм–это величина погрешности линейных измерений при помощи линейки

циркуля-измерителя и линейного масштаба;

• Измерение отрезков с помощью линейного масштаба проводят в следующем порядке:

• взять в раствор циркуля-измерителя отрезок, который необходимо измерить;

• приложить раствор циркуля к основанию линейного масштаба, при этом его правую ножку совместить с одним из штрихов основания так, чтобы левая ножка поместилась на основании влево от нуля (на дробном основании);

• посчитать количество целых и десятых долей основания масштаба:

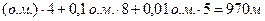(О.М.) - основание масштаба