Выполнение лабораторной работы
1. Записать таблицы истинности для функций (согласно варианту задания).
2. На основе таблицы истинности записать логические выражения каждой функции в виде СКНФ и СДНФ.
3. Собрать схему на логических элементах «И», «ИЛИ». «И-НЕ» «ИЛИ-НЕ», «НЕ». Получить временные диаграммы, продемонстрировать выполненную в системе Multisim работу преподавателю.
4. Оформить отчет. Отчет оформляется на том же занятии. В отчете приводятся определения основных функций алгебры логики, таблицы истинности, схема исследования, временные диаграммы входных и выходных сигналов каждой схемы. В заключение, в отчете необходимо сделать вывод о соответствии полученных временных диаграмм таблице истинности.
5. Если какие-то пункты задания студент не успел выполнить во время занятия, то эти пункты должны быть выполнены самостоятельно и представлены преподавателю на следующем занятии.
Варианты заданий к лабораторной работе
Варианты заданий к лабораторной работе приведены в таблице 2.2.2,
Таблица. 2.2.2
| Номер варианта | F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | F15 |
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + |
Вопросы для подготовки к отчету:
1. Что такое логическая функция и логическая переменная?
2. Как получены 16 простейших функций 2-х аргументов?
3. Что такое дизъюнкция?
4. Как записывается функция в дизъюнктивной нормальной форме?
5. Что такое конъюнкция?
6. Как записывается функция в конъюнктивной нормальной форме?
7. Как можно представить логическую функцию при помощи таблицы истинности?
8. Как запрограммировать генератор слов, чтобы исследовать функцию двух переменных на всех наборах переменных?
3. Лабораторная работа № 3
Доказательство основных тождеств булевой алгебры
Цель работы: Исследование тождеств алгебры логики, применяемых для преобразования логических выражений.
Задание: Построить схемы – аналоги логических уравнений двух частей заданных тождеств. Доказать тождество экспериментально, средствами Multisim.
Теоретическое введение:
Законы алгебры логики базируются на аксиомах:
| 0 х 0 = 0; | 0 + 0 = 0; |
| 0 х 1 = 0; | 0 + 1 = 1; |
| 1 х 0 = 0; | 1+ 0 = 1; |
| 1 x 1 = 1; | 1 + 1 = 1. |
Из аксиом следует, что:
Х х 1 = Х: Х + 0 = Х :
X х 0 = 0; Х + 1 = 1;
X х Х = Х; Х + Х = Х – закон тавтологии;
X х X* = 0; X + X* = 1 – закон дополнительных элементов (здесь и в дальнейшем символ «*» обозначает инверсию).
1) XY = YX; 2) X + Y = Y + X – коммуникативный закон;
3) X(YZ) = (XY)Z; 4) X + (Y+Z) = (X +Y) + Z – ассоциативный закон;
5) X + YZ = (X + Y)(X + Z); 6) X (Y + Z) = XY + XZ – дистрибутивный закон;
7) XY + X*Y = Y; 8) (X + Y) x (X* + Y) = Y –закон склеивания;
9) X(X + Y) = X; 10) X + (XY) = X-закон поглощения;
11) X* x Y* = (X + Y)*; 12) X* + Y* = (X x Y)* - закон (правило) де Моргана.
X = X** - отрицание отрицания (двойное отрицанис).
Выполнение лабораторной работы
Для выполнения работы необходимо использовать опыт предыдущей лабораторной работы в части, касающейся построения технических аналогов логических уравнений. Для доказательства тождества необходимо построить схемы – аналоги логических уравнений обеих частей тождества и проанализировать выходные параметры каждой схемы.
Используя пакет Multisim собрать схемы, соответствующие обеим частям тождества. С помощью анализа доказать тождество (проверку произвести на всех возможных наборах переменных.
Составить отчет о выполнении лабораторной работы. В отчет включить схемы и диаграммы входных и выходных сигналов для каждой из исследуемых схем. Сделать заключение.
Варианты заданий к лабораторной работе
Варианты заданий к лабораторной работе приведены в таблице 2.2.3.
Таблица 2.2.3.
| N варианта/ функция | F 1 | F 2 | F 3 | F 4 | F 5 | F 6 | F 7 | F 8 | F 9 | F10 | F 11 | F 12 |
| + | + | + | ||||||||||
| + | + | + | ||||||||||
| + | + | + | ||||||||||
| + | + | + | ||||||||||
| + | + | + | ||||||||||
| + | + | + | ||||||||||
| + | + | + | ||||||||||
| + | + | + | ||||||||||
| + | + | + | ||||||||||
| + | + | + | ||||||||||
| + | + | + | ||||||||||
| + | + | + | ||||||||||
| + | + | + | ||||||||||
| + | + | + | ||||||||||
| + | + | + | ||||||||||
| + | + | + |
Вопросы для подготовки к отчету:
1. Чем отличаются операции склеивания и поглощения? Докажите путем логических заключений и преобразований, что эти операции действительно выполняются.
2. Докажите путем логических заключений и преобразований, что правила де Моргана действительно выполняются.
4. Лабораторная работа № 4
Синтез логических схем и их исследование
Цель работы: Приобретение навыков синтеза логических схем и их реализации в определенном базисе.
Задание:Записать логические выражения функций в СДНФ и в СКНФ.
Минимизировать полученные выражения с помощью карты Карно.
Перевести выражение в базис И-НЕ или в базис ИЛИ-НЕ (в зависимости от варианта задания). Построить схему устройства в соответствующем базисе.
Теоретическое введение
Все логические схемы подразделяются на комбинационные схемы и цифровые автоматы (или последовательностные схемы).
В комбинационной схеме любой выходной сигнал в любой момент времени однозначно определяется входными сигналами. Результат зависит только от комбинации входных сигналов и вырабатывается сразу при подаче входной информации. Закон функциональности комбинационной схемы определен, если задано соответствие между ее входными и выходными комбинациями.
В цифровых схемах последовательностного типа (имеют память), выходное состояние в любой момент времени определяется как сигналами на входах цифрового автомата, так и его предыдущим состоянием.
Функции алгебры логики могут быть заданы в виде:
1. Таблицы истинности (таблицы состояний).
2. Структурной формулы (логического выражения), описывающей функциональную связь между входными и выходными переменными.
3. Временных диаграмм.
Порядок синтеза комбинационных схем и цифровых автоматов:
1. Словесная формулировка задачи, в которой оговаривается число входных и выходных переменных и функциональные связи между ними.
2. Составление таблицы истинности синтезируемой функции.
3. Запись функции (или функций) в виде логического выражения (или системы логических уравнений).
4. Минимизация функции.
5. Построение логической схемы из конкретных логических элементов с использованием логического уравнения в минимальной форме.
Рассмотрим синтез функции на примере.
Пусть функция 3-х переменных задана таблицей истинности (таблица 2.4.1).
Таблица 2.4.1.
| Номер набора | Входы | Выход | ||
| Х3 | Х2 | Х1 | F | |
Каждую конкретную комбинацию аргументов называют набором. Для краткости набор записывают в виде двоичного числа, цифрами которого являются значения аргументов. Для паргументов существует N = 2n наборов.
Если неизвестно, какие значения принимает функция на всех наборах аргументов, то она называется недоопределенной, или не полностью определенной (частично), а комбинации аргументов, для которых функция не определена, – запрещенными наборами. Значения функции на запрещенных наборах можно задать по своему усмотрению (доопределить функцию). Этот прием используется при минимизации функций.
После того как таблица истинности составлена, находят алгебраическую форму этой функции. На следующем этапе функцию преобразуют в простейшую форму, которую потом реализуют с помощью соответствующих электрических схем.
Для записи логической функции в дизъюнктивной нормальной форме поступают следующим образом:
1. В таблице истинности выделяют строки, в которых булева функция имеет значение 1.
2. Для каждой такой строки составляют конъюнкцию всех входных переменных, причем записывают сомножитель без инверсии, если переменная принимает значение 1 и с инверсией, если 0. Составляют столько конъюнкций всех аргументов, сколько имеется строк в таблице истинности, в которых функция равна 1. Каждая такая конъюнкция называется конституентой единицы.
Таким образом функцию F запишем в СДНФ:FСДНФ (X1,X2,X3) = X1*·X2*·X3*+ X1·X2*·X3* + X1*·X2*·X3 +X1*·X2·X3 + X1·X2·X3.
Функция представлена суммой групп конституент единицы. Каждая группа состоит из произведения, в которую входят все переменные.
Если схема имеет несколько выходов, то каждый выход описывается своей функцией. Такая система функций называется системой собственных функций.
Для записи функции в коньюнктивной нормальной форме (СКНФ) пользуемся правилом: для каждого набора переменных, при котором функция равна 0, записывается сумма, в которой с отрицанием берутся переменные, имеющие значение 1.
FСКНФ (X1,X2,X3) = (X1+ X2* +X3) (X1*+X2*+X3) (X1*+ X2 +X3*)
Теперь полученные функции необходимо минимизировать.
Простые функции можно минимизировать, используя законы склеивания и поглощения.
Для FСДНФ (X1,X2,X3) склеиваются первый и второй члены, получаем (X2*·X3*), склеиваем первый и третий члены, получаем (X1*·X2*), четвертый и пятый дают (X2·X3).
Получаем минимизированную функцию:
FМДФ (X1,X2,X3) = (X2*· X3*) + (X1*·X2*) + (X2·X3)
Для FСКНФ (X1,X2,X3) склеиваются пе6рвый и второй члены функции, третий остается без изменений..
Получаем минимизированную функцию:
FМКФ (X1,X2,X3) = (X2* +X3) (X1*+X2+ X3*)
Для минимизации функций широко применяют карты Карно. Карта Карно представляет собой некоторую модификацию таблицы истинности без изменения логики функционирования схемы. Входные переменные в картах Карно представлены в виде кода Грея (соседние кодовые комбинации отличаются только одним разрядом). Верхняя и нижняя строки, а также правый и левый столбец являются соседними, т.е. карту Карно можно сворачивать в кольцо в каждом направлении.
Минимизация осуществляется за счет операций склеивания и поглощения.
Склеивание происходит в соответствии со следующими правилами:
- склеивание можно осуществлять по единицам (для ДНФ) или по нулям (для КНФ). Причем склеиваемые области (импликаты) должны содержать только единицы для ДНФ (или только нули для КНФ );
- объединяются только прямоугольные области с числом единиц (нулей) 2n, где n – целое число;
- объединяются только соседние по горизонтали или вертикали клетки (крайние клетки каждой строки и каждого столбца граничат между собой);
- для получения оптимального результата число областей объединения (импликат) должно быть как можно меньше, а число клеток в области должно быть как можно больше;
- одна ячейка может входить сразу в несколько областей.
C учетом этих правил сам процесс минимизации можно описать следующим образом: после составления карты Карно и выделения областей смежных единиц необходимо внутри каждой области исключить переменные, дополняющие друг друга, а оставшиеся члены объединить функцией ИЛИ для ДНФ. Следует отметить, что результатом минимизации могут быть эквивалентные друг другу формы, которые соответствуют разным способам покрытия карты Карно областями. На рис. 2.4.1 показана карта Карно для исследуемой нами функции, на которой выделены 3 области из двух рядом стоящих единиц. Для минимизации функции в дизъюнктивной нормальной форме выпишем не изменяющиеся переменные.

Рис. 2.4.1. Карта Карно для трех переменных, минимизация функции в ДНФ, выделены 3 области.
FМДФ (X1,X2,X3) = (X2*· X3*) + (X1*·X2*) + (X2·X3)
Первая выделенная область дает первый член функции, вторая– второй и третья – третий.
В конъюнктивной форме объединяем рядом стоящие нули (рис.2.4.2). Выделили только одну область.

Рис. 2.4.2. Карта Карно для трех переменных, минимизация функции в КНФ, выделена 1 область
Запишем теперь функцию, выписывая не изменяющуюся часть в выделенной области с инверсией переменных. Еще одна конституента нуля не имеет соседних нулей и будет внесена в минимизированную форму без изменения. В результате получим:
FМКФ (X1,X2,X3) = (X2* +X3) (X1*+X2+ X3*)
На основе полученных выражений можно составить схему устройства, реализующего заданную функцию. Схема устройства, полученная на основе СДНФ, изображена на рис. 2.4,3 а на основе СКНФ на рис. 2.4.4.
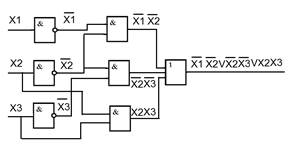
Рис. 2.4.3. Схема устройства, полученная на основе минимизации СДНФ
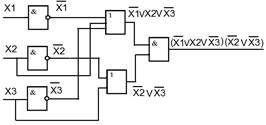
Рис. 2.4.4. Схема устройства, полученная на основе минимизации СКНФ
