Мощность однофазного переменного тока. Коэффициент мощности
Рис.2.35 изображает неразветвлённую цепь с активным сопротивлением R и индуктивностью L.

Рис.2.35. Цепь переменного тока с активным сопротивлением и индуктивностью
Пусть мгновенный ток в цепи изменяется по закону 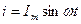 . Тогда мгновенное напряжение на активном сопротивлении
. Тогда мгновенное напряжение на активном сопротивлении  , так как на этом участке напряжение и ток совпадают по фазе. Напряжение на катушке индуктивности
, так как на этом участке напряжение и ток совпадают по фазе. Напряжение на катушке индуктивности  , поскольку на индуктивности напряжение опережает по фазе ток на угол
, поскольку на индуктивности напряжение опережает по фазе ток на угол 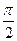 .
.
Построим для действующих значений напряжения и тока векторную диаграмму для рассматриваемой цепи (рис. 2.36).
Векторы  и
и  образуют треугольник напряжений. Выведем закон Ома для этой цепи. Из треугольника напряжений имеем
образуют треугольник напряжений. Выведем закон Ома для этой цепи. Из треугольника напряжений имеем  . Но
. Но  , а
, а  , где
, где  - индуктивное сопротивление, следовательно:
- индуктивное сопротивление, следовательно:
 , откуда
, откуда
 . (2.36)
. (2.36)

Рис.2.36. Векторная диаграмма действующих значений тока и напряжения цепи переменного тока с активным сопротивлением и индуктивностью
Введем обозначение  , где Z - полное сопротивление цепи. Тогда выражение закона Ома примет вид:
, где Z - полное сопротивление цепи. Тогда выражение закона Ома примет вид:
 . (2.37)
. (2.37)
Полное сопротивление Z можно определить из треугольника сопротивлений (рис. 2.37).

Рис.2.37. Треугольник сопротивлений цепи переменного тока с активным сопротивлением и индуктивностью
Сдвиг фаз 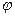 между током и напряжением определяется из треугольника сопротивлений:
между током и напряжением определяется из треугольника сопротивлений:
 , (2.38)
, (2.38)
 . (2.39)
. (2.39)
Поскольку вектор  сдвинут по фазе относительно вектора
сдвинут по фазе относительно вектора  на угол
на угол 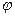 против часовой стрелки, этот угол имеет положительное значение.
против часовой стрелки, этот угол имеет положительное значение.
Если  (рис.2.38) , то мгновенная мощность
(рис.2.38) , то мгновенная мощность  . Для действующих значений произведение
. Для действующих значений произведение  , откуда
, откуда  . Выражение
. Выражение  . Исходя из этого,
. Исходя из этого,
 . (2.40)
. (2.40)
Таким образом, мгновенная мощность переменного тока может быть представлена в виде постоянной величины  и, изменяющейся около неё с двойной частотой, величины
и, изменяющейся около неё с двойной частотой, величины  .
.
Введем понятие средней или активной мощности:
 . (2.41)
. (2.41)
Активная мощность характеризует расход энергии на активном сопротивлении.
Реактивная мощность характеризует обмен энергий между индуктивной катушкой и источником:
 . (2.42)
. (2.42)
Полная мощность оценивает предельную мощность нагрузки:
 . (2.43)
. (2.43)

Рис.2.38. Зависимости мгновенных значений напряжения, тока и мощности цепи переменного тока с активным сопротивлением и индуктивностью
Совокупность всех мощностей можно определить из треугольника мощностей (рис. 2.39).

Рис.2.39. Треугольник мощностей
Так:  Обозначим коэффициент мощности в виде соотношения
Обозначим коэффициент мощности в виде соотношения  .
.
Коэффициент мощности cosφ изменяется от 0 до 1. По его величине судят, какую часть полной мощности составляет активная мощность. На практике стремятся к увеличению cosφ.
3. Трёхфазные электрические цепи
3.1. Преимущество трёхфазного тока. Принцип получения трёхфазной ЭДС
В современной электроэнергетике наибольшее распространение получили трёхфазные цепи. Они обладают рядом преимуществ перед однофазными цепями переменного тока. Среди преимуществ можно отметить экономичность производства и передачи электрической энергии. По сравнению с однофазными электрическими машинами мощность трёхфазных машин повышается в 1,5 раза при одинаковых габаритах. При этом возможно простое получение вращающегося магнитного поля, необходимого для 3-х фазного асинхронного двигателя, самого распространенного из двигателей переменного тока, а также получение в одной установке двух эксплуатационных напряжений (фазного и линейного).
На рис.3.1 изображена модель трёхфазного генератора, с помощью которой можно пояснить принцип получения трёхфазной ЭДС.
На неподвижном статоре генератора размещаются три одинаковые и сдвинутые друг относительно друга на угол  по магнитным осям обмотки, которые называются фазными обмотками генератора.
по магнитным осям обмотки, которые называются фазными обмотками генератора.
Начала обмоток обозначены буквами A,B,C, концы - X,Y,Z. ЭДС в неподвижных витках обмоток статора индуктируются в результате пересечения этих витков магнитным полем, возбуждаемым током вращающегося ротора (ротор с обмоткой условно изображен в виде постоянного магнита с полюсами N и S). 
Расположенная на роторе обмотка возбуждения питается от источника постоянного напряжения.

Рис.3.1. Модель трёхфазного генератора
При вращении ротора с равномерной угловой скоростью 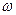 , в обмотках фаз статора индуктируются периодически изменяющиеся синусоидальные ЭДС
, в обмотках фаз статора индуктируются периодически изменяющиеся синусоидальные ЭДС  ,
,  ,
,  одинаковой частоты. Мгновенные ЭДС индуктивных элементов сдвинуты по фазе на угол
одинаковой частоты. Мгновенные ЭДС индуктивных элементов сдвинуты по фазе на угол  . За условное положительное направление ЭДС в каждой фазе принимается направление от конца к началу (рис.3.2).
. За условное положительное направление ЭДС в каждой фазе принимается направление от конца к началу (рис.3.2).

Рис.3.2. Направления мгновенных ЭДС обмоток статора трёхфазной цепи
Совокупность ЭДС, напряжений и токов трёхфазной цепи называется трёхфазной системой. При сдвиге фаз между ЭДС, напряжениями и токами на угол  и равенстве их амплитудных значений трёхфазная система называется симметричной. Симметричная трехфазная система может изображаться тригонометрическими функциями, графиками, векторами.
и равенстве их амплитудных значений трёхфазная система называется симметричной. Симметричная трехфазная система может изображаться тригонометрическими функциями, графиками, векторами.
Если принять, что мгновенная ЭДС фазы A в нулевой момент времени равна  , то мгновенные ЭДС в фазах индуктивных элементов В и С будут определяться тригонометрическими функциями
, то мгновенные ЭДС в фазах индуктивных элементов В и С будут определяться тригонометрическими функциями  и
и  .
.
Мгновенные значения ЭДС трёхфазного генератора графически выразятся в виде трёх синусоид, сдвинутых друг относительно друга по фазе на угол  (рис.3.3).
(рис.3.3).

Рис.3.3. Мгновенные значения ЭДС трёхфазного генератора
При симметричной нагрузке геометрическая сумма трёх симметричных ЭДС фаз равна 0.  или
или  . Векторная диаграмма значений ЭДС симметричного трехфазного генератора представлена на рис.3.4.
. Векторная диаграмма значений ЭДС симметричного трехфазного генератора представлена на рис.3.4.

Рис.3.4. Векторная диаграмма значений ЭДС симметричного трехфазного генератора
Частота вращения ротора синхронного генератора равна частоте вращения поля статора и сохраняется постоянной, независимо от нагрузки. Частота ЭДС генератора f зависит от числа пар полюсов ротора p и частоты его вращения n, то есть f = pn, при f = 50 Гц, p = 1, n = 50 об/c = 3000 об/мин. В качестве первичных двигателей вращения генераторов используют дизели или турбины.
