Тема IV.2. Случайные события и их вероятности

1. Случайные события. Основные понятия: события. Испытания; достоверные, невозможные; случайные события; равносильные, противоположные события. Элементарные действия над событиями: сумма, произведение, разность. Понятия совместных и несовместных событий. Полная группа событий. Элементарные события.

2. Вероятность события. Понятие вероятности события: классическая вероятность события, статистическое определение вероятности, геометрическая вероятность.

3. Элементы комбинаторики: перестановки, размещение, сочетание.

4. Основные теоремы теории вероятностей: теорема сложения, теорема умножения. Условные вероятности. Формула полной вероятности. Формула Байеса.

5. Приближенные формулы для вычисления вероятности при проведении n независимых испытаний, в результате которых может произойти событие A с одной и той же вероятностью P: схема Бернулли, локальная и интегральные теоремы Муавра-Лапласа, формула Пуассона.

Примеры: 1. Примеры событий (выпадение герба при подбрасывании монеты; выигрыш автомобиля по лотерейному билету; появление бракованной детали на сборке изделия; приход группы в полном составе на лекцию по математике; попадание мяча в ворота после удара футболиста и т.д.); примеры достоверных событий (выпадение числа очков менее 10 при однократном бросании игральной кости; отсутствие солнца на московском небе в 24 часа); примеры невозможных событий (выпадение 10 очков при однократном бросании игральной кости; встреча на улице с человеком пятиметрового роста); примеры случайного события (выпадение 3 очков при однократном бросании игральной кости; завершение футбольного матча «Локомотив»-ЦСКА со счетом 1:1); примеры равновозможных событий (А – «присутствие Иванова на данной лекции по математике, В – «присутствие Петрова на этой же лекций); примеры противоположных событий (А – «попадание стрелка в «десятку» при выстреле из винтовки по мишени», 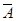- «попадание в любую другую область мишени или за её пределы»); примеры совместных и невместных событий (выпадение 2-х и 3-х очков при однократном бросании игральной кости; получение оценок «отлично» и «неудовлетворительно» на одном и том же экзамене)

2. Найти вероятность выпадения четного числа очков при бросании игральной кости один раз.

3. В ящике перемешаны 20 годных деталей и 5 бракованных. Сборщик наугад достает одну деталь. Чему равна вероятность, что она бракованная?

4. Английский ученый Э.Пирсон произвел 23000 бросаний монеты. При этом герб появился 11512 раз. Найти частоту появления герба в опыте ученого.

5. Два лица x и y условились встретиться в определенном листе между 12 часами и часом, при этом пришедший первым ждет другого в течение 20 минут, после чего уходит. Чему равна вероятность встречи лиц x и y, если приход каждого из них в течение указанного часа может произойти наудачу и моменты прихода независимы?

6. На книжной полке стоят 5 книг. Сколькими способами можно расположить эти книги на полке?

7. Сколькими способами из 10 кандидатов можно выбрать:

а) председателя, зам.председателя и секретаря?

б) трех делегатов на конференцию?

8. Из 6 карточек разрезной азбуки сложено слово АНАНАС. Найти вероятность того, что из 3 наугад выбранных и разложенных в порядке появления карточек можно получить слово САН.

9. Пусть в группе из 27 туристов. 17 человек владеют английским языком. 6 – французским, а 2 – обоими языками. Найти вероятность того, что случайно выбранный из группы турист владеет по крайней мере одним из этих языков.

10. Три стрелка стреляют в цель независимо друг от друга. Вероятность попадания для первого стрелка при отдельном выстреле равна 0,6; второго – 0,7 и третьего – 0,75. Найти вероятность попадания в цель хотя бы одного стрелка, если каждый сделает по одному выстрелу.

11. На складе университета хранится 28 одинаковых упаковок писчей бумаги. Известно, что в четырех из них содержится бумага более низкого качества. Случайным образом выбирают три упаковки бумаги. Вычислить вероятность того, что среди них:

а) нет упаковок с бумагой более низкого качества,

б) есть только одна упаковка бумаги более низкого качества,

в) есть хотя бы одна упаковка такой бумаги.

12. Магазин получает электрические лампочки с двух заводов, причем доля первого завода составляет 25%. Известно, что доля брака на этих заводах равна соответственно 5% и 10% от всей выпускаемой продукции. Продавец наугад берет одну лампочку. Какова вероятность того, что она окажется бракованной?

13. Вероятность выигрыша по лотерейному билету равна 0,05. какова вероятность того, что среди купленных 10 билетов окажутся 2 выигрышных?

14. В ходе проверки аудитор случайным образом отбирает 10 счетов. Найти вероятность того, что он обнаружит 1 счет с ошибкой, если в среднем 3% счетов содержат ошибки.

15. Арбуз оказывается неспелым с вероятностью q=0,25. Найти вероятность того, что в партии из 768 арбузов количество спелых арбузов будет

а) 680;

б) от 564 до 60

Литература: [№ 3],[№4],[№5],[№7],[№15],[№22].