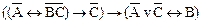Правило для упрощения логических выражений с помощью СДНФ или СКНФ
1. Составьте СДНФ или СКНФ данной логической функции (выбор СКНФ или СДНФ зависит от их сложности).
2. Упростите ее с помощью основных законов и равносильностей.
 | Прочитайте текст. Во время чтения текста выделите новую (важную) для вас информацию. |
 | Задания: 1. Заполните таблицу:
2. Запишите порядок упрощения логической функции с использованием совершенных форм. | ||||
 | Решите задачи:
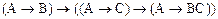 ? ? |
Тема 5.5 Решение логических задач
Основные понятия: основные способы решения логических задач, решение логических задач средствами алгебры логики, табличный способ решения логических задач.
Условные обозначения:
 - задания до чтения текста - задания до чтения текста |  - задания во время чтения - задания во время чтения |  - задания после чтения - задания после чтения |
 | Прочитайте текст. Во время чтения текста составьте таблицу:
|
Логика широко применяется при решении логических задач. Разнообразие логических задач очень велико. Способов их решения тоже немало. Но наибольшее распространение получили следующие три способа решения логических задач:
средствами алгебры логики;
табличный;
с помощью рассуждений.
Познакомимся с ними поочередно.
I. Решение логических задач средствами алгебры логики
Обычно используется следующая схема решения:
1. изучается условие задачи;
2. вводится система обозначений для логических высказываний;
3. конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи;
4. определяются значения истинности этой логической формулы;
5. из полученных значений истинности формулы определяются значения истинности введённых логических высказываний, на основании которых делается заключение о решении.
Задача 1 Трое друзей, болельщиков автогонок "Формула-1", спорили о результатах предстоящего этапа гонок.
— Вот увидишь, Шумахер не придет первым, — сказал Джон. Первым будет Хилл.
— Да нет же, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым.
Питер, к которому обратился Ник, возмутился:
— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?
Решение.
Введем обозначения для логических высказываний: Ш — победит Шумахер; Х — победит Хилл; А — победит Алези.
Реплика Ника "Алези пилотирует самую мощную машину" не содержит никакого утверждения о месте, которое займёт этот гонщик, поэтому в дальнейших рассуждениях не учитывается.
Зафиксируем высказывания каждого из друзей:
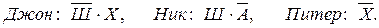 |
Учитывая то, что предположения двух друзей подтвердились, а предположения третьего неверны, запишем и упростим истинное высказывание 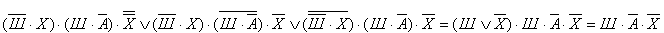
Высказывание 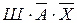 истинно только при Ш=1, А=0, Х=0.
истинно только при Ш=1, А=0, Х=0.
Ответ. Победителем этапа гонок стал Шумахер.
II. Решение логических задач табличным способом
При использовании этого способа условия, которые содержит задача, и результаты рассуждений фиксируются с помощью специально составленных таблиц.
Задача 2. В симфонический оркестр приняли на работу трёх музыкантов: Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе.
Известно, что:
1. Смит самый высокий;
2. играющий на скрипке меньше ростом играющего на флейте;
3. играющие на скрипке и флейте и Браун любят пиццу;
4. когда между альтистом и трубачом возникает ссора, Смит мирит их;
5. Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
Решение.
Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание. Так как музыкантов трое, инструментов шесть и каждый владеет только двумя инструментами, получается, что каждый музыкант играет на инструментах, которыми остальные не владеют. Из условия 4 следует, что Смит не играет ни на альте, ни на трубе, а из условий 3 и 5, что Браун не умеет играть на скрипке, флейте, трубе и гобое. Следовательно, инструменты Брауна — альт и кларнет. Занесем это в таблицу 5.10, а оставшиеся клетки столбцов "альт" и "кларнет" заполним нулями.
Таблица 1
| скрипка | флейта | альт | кларнет | гобой | труба | |
| Браун | ||||||
| Смит | ||||||
| Вессон |
Из таблицы видно, что на трубе может играть только Вессон. Из условий 1 и 2 следует, что Смит не скрипач. Так как на скрипке не играет ни Браун, ни Смит, то скрипачом является Вессон. Оба инструмента, на которых играет Вессон, теперь определены, поэтому остальные клетки строки "Вессон" в таблице 2 можно заполнить нулями.
Таблица 2
| скрипка | флейта | альт | кларнет | гобой | труба | |
| Браун | ||||||
| Смит | ||||||
| Вессон |
Из таблицы 2 видно, что играть на флейте и на гобое может только Смит. Получим итоговую таблицу 3
Таблица 3
| скрипка | флейта | альт | кларнет | гобой | труба | |
| Браун | ||||||
| Смит | ||||||
| Вессон |
Ответ: Браун играет на альте и кларнете, Смит — на флейте и гобое, Вессон — на скрипке и трубе.
III. Решение логических задач с помощью рассуждений
Этим способом обычно решают несложные логические задачи.
Задача 3. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?
Решение.
Имеется три утверждения:
1. Вадим изучает китайский;
2. Сергей не изучает китайский;
3. Михаил не изучает арабский.
Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно. Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно. Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.
Ответ: Сергей изучает китайский язык, Михаил — японский, Вадим — арабский.
 | Решите задачи: 1. Коля, Боря, Вова и Юра заняли первые 4 места в спортивных соревнованиях. На вопрос, какие они места заняли, они ответили: a) Коля не занял, ни первое, ни четвертое место b) Боря занял второе место c) Вова не был последним. 2. В кафе встретились три друга Белов, Чернов и Рыжов. «Замечательно, что у всех нас разный цвет волос, но ни у одного он не соответствует фамилии», - заметил черноволосый. «Ты прав», - сказал Белов. Какого цвета волосы у Рыжова? 3. Известно, что одно из двух высказываний «Король Пик и дама Пик не в своем уме» и «Дама Пик не в своем уме» - истинно, а второе ложно. Выяснить, кто в своем уме. 4. На вокзале на табло первого перрона была надпись «Вологда», на табло второго – «Псков или Новгород», на табло третьего – «Псков». От пассажиров поступили жалобы, что поезда едут не туда, куда указывали надписи. На каком перроне какой поезд стоял. 5. Кто из студентов A, B, C, D играет, а кто не играет в шахматы, если известно, что a) если A или B играют, то C не играет; b) если B не играет, то играют C и D; c) C играет. |
Модуль 6.
Алгоритмизация.
Тема 6.1 Понятие алгоритма. Свойства алгоритма. Способы записи алгоритмов.
Основные понятия: алгоритм, свойства алгоритма, блок-схема, код, псевдокод, язык программирования.
Условные обозначения:
 - задания до чтения текста - задания до чтения текста |  - задания во время чтения - задания во время чтения |  - задания после чтения - задания после чтения |
 | Вы постоянно сталкиваетесь с понятием алгоритма в различных сферах деятельности человека (кулинарные книги, инструкции по использованию различных приборов, правила решения математических задач...). Обычно мы выполняем привычные действия не задумываясь, механически. Например, вы хорошо знаете, как открывать ключом дверь. Однако, чтобы научить этому малыша, придется четко разъяснить и сами эти действия и порядок их выполнения. Составьте инструкцию для отпирания двери ключом: 1 шаг (действие): 2 шаг (действие): 3 шаг (действие): … |
 | Прочитайте текст. Сделайте конспект . |
Появление алгоритмов связывают с зарождением математики. Более 1000 лет назад (в 825 году) ученый из города Хорезма Абдулла (или Абу Джафар) Мухаммед бен Муса аль-Хорезми создал книгу по математике, в которой описал способы выполнения арифметических действий над многозначными числами. Само слово алгоритм возникло в Европе после перевода на латынь книги этого математика.
Алгоритм – описание последовательности действий (план), строгое исполнение которых приводит к решению поставленной задачи за конечное число шагов.
Если вы внимательно оглянитесь вокруг, то обнаружите множество алгоритмов которые мы с вами постоянно выполняем. Мир алгоритмов очень разнообразен. Несмотря на это, удается выделить общие свойства, которыми обладает любой алгоритм.
Свойства алгоритмов:
1. Дискретность (алгоритм должен состоять из конкретных действий, следующих в определенном порядке);
2. Детерминированность (любое действие должно быть строго и недвусмысленно определено в каждом случае);
3. Конечность (каждое действие и алгоритм в целом должны иметь возможность завершения);
4. Массовость (один и тот же алгоритм можно использовать с разными исходными данными);
5. Результативность (отсутствие ошибок, алгоритм должен приводить к правильному результату для всех допустимых входных значениях).
На практике чаще всего встречаются следующие формы представления алгоритмов:
• словесная – записывается на естественном языке;
• графическая – с помощью изображения из графических символов;
• псевдокоды – полуформализованные описания алгоритмов на некотором условном алгоритмическом языке, которые включают в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.;
• программная – тексты на языках программирования.
Словесный способ записи алгоритмов является описанием последовательных этапов обработки данных. Алгоритм может быть задан в произвольном изложении на естественном языке. Например, алгоритм нахождения наибольшего общего делителя двух натуральных чисел можно представить как следующую последовательность действий:
1) задание двух чисел;
2) если числа равны, то выбор любого из них в качестве ответа и остановка, в противном случае – продолжение выполнения алгоритма;
3) определение большего из чисел;
4) замена большего из чисел разностью большего и меньшего из чисел;
5) повтор алгоритма с шага 2.
Приведенный алгоритм используется для любых натуральных чисел и должен приводить к решению поставленной задачи.
Словесный способ не имеет широкого распространения, так как обладает некоторыми недостатками:
• данные описания строго не формализуемы;
• отличаются многословностью записей;
• допускают неоднозначность толкования отдельных предписаний.
Графический способ представления алгоритмов оказывается более компактным и наглядным по сравнению со словесным. При данном виде представления алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению некоторого числа действий.
Для графического представления алгоритм использует изображение в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Это графическое представление называется схемой алгоритма, или блок-схемой.
В блок-схеме каждый из типов действий (ввод исходных данных, вычисление значений выражений, проверка условий, управление повторением действий, окончание обработки и т. п.) соответствует геометрической фигуре, представленной в виде блочного символа. Блочные символы соединены линиями переходов, которые определяют очередность выполнения действий.
| Вид стандартного графического объекта | Назначение | ||
 | Начало алгоритма | ||
 | Конец алгоритма | ||
| Выполняемое действие записывается внутри прямоугольника | ||
 | Условие выполнения действий записывается внутри ромба | ||
 | Счетчик (количество повторов) | ||
 | Последовательность выполнения действий. |
Псевдокод является системой обозначений и правил, которая предназначена для единообразной записи алгоритмов. Он занимает промежуточное место между естественным и формальным языками. С одной стороны, псевдокод похож на обычный естественный язык, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, благодаря чему запись алгоритма приближается к общепринятой математической записи.
В псевдокоде не применяются строгие синтаксические правила для записи команд, которые присущи формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя. Однако в псевдокоде чаще всего имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. Например, в псевдокоде, также каки в формальных языках, существуют служебные слова, смысл которых определен раз и навсегда.
Например, алгоритмы на алгоритмическом языке записываются с помощью служебных слов, представленных в таблице 1.7.
Таблица 1.7. Служебные слова алгоритмического языка.
| алг(алгоритм) | сим (символьный) | дано | да | нет |
| арг(аргумент) | лит (литерный) | надо | для | при |
| рез(результат) | лог(логический) | если | от | до |
| нач(начало) | таб (таблица) | то | знач | выбор |
| кон(конец) | нц(начало цикла) | иначе | и | или |
| цел (целый) | кц (конец цикла) | всё | ввод | вывод |
| вещ (вещественный) | длин(длина) | пока | утв | не |
Общий вид алгоритма:
алгназвание алгоритма (аргументы и результаты)
даноусловия применимости алгоритма
надоцель выполнения алгоритма
начописание промежуточных величин
последовательность команд (тело алгоритма)
Кон.
Часть алгоритма от слова алгдо слова начназывается заголовком, а часть, заключённая между словами начи кон— телом алгоритма.
Единый или формальный подход к определению псевдокода не существует, поэтому используются различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций.
Программная форма представления алгоритмов предполагает, что алгоритм, предназначенный для исполнения на компьютере, должен быть записан на понятном ему языке. В этом случае язык для записи алгоритмов должен быть формализован. Такой язык принято называть языком программирования, а запись алгоритма на этом языке — программой.
Стадии создания алгоритма:
1. Алгоритм должен быть представлен в форме, понятной человеку, который его разрабатывает.
2. Алгоритм должен быть представлен в форме, понятной тому объекту (в том числе и человеку), который будет выполнять описанные в алгоритме действия.
Исполнитель алгоритма - объект, который выполняет алгоритм.
Идеальными исполнителями являются машины, роботы, компьютеры...
Исполнитель способен выполнить только ограниченное количество команд. Поэтому алгоритм разрабатывается и детализируется так, чтобы в нем присутствовали только те команды и конструкции, которые может выполнить исполнитель.
Исполнитель, как и любой объект, находится в определенной среде и может выполнять только допустимые в нем действия. Если исполнитель встретит в алгоритме неизвестную ему команду, то выполнение алгоритма прекратится.
Компьютер – автоматизированный исполнитель алгоритмов.
Алгоритм, записанный на «понятном» компьютеру языке программирования, называется программой.
Программирование - процесс составления программы для компьютера. Для первых ЭВМ программы записывались в виде последовательности элементарных операций. Это была очень трудоемкая и неэффективная работа. Поэтому в последствии были разработанные специальные языки программирования. В настоящее время существует множество искусственных языков для составления программ. Однако так и не удалось создать идеальный язык, который бы устроил бы всех.
 | Ответьте письменно на вопросы и выполните задания: 19. Является ли инструкция, написанная Вами в начале работы с текстом, алгоритмом. Ответ обоснуйте. 20. Найдите ошибку в определении понятия «алгоритм»: «Алгоритм – это последовательность шагов деятельности». Ответ обоснуйте. 21. Что означает свойство алгоритма «массовость»? 22. На какие свойства алгоритма окажет влияние выбор того или иного исполнителя для решения одной и той же задачи? 23. Можно ли считать исполнителем алгоритма: (а) человека, ведущего запись текста под диктовку, (b) компьютер; (с) компьютерную программу, (d) дрессированное животное. Ответы обоснуйте. 24. Составьте словесный алгоритм сложения в столбик двух натуральных чисел. 25. Есть двое песочных часов: на 3 минуты и на 8 минут. Для приготовления эликсира бессмертия его нужно варить 7 минут. Как это сделать. Придумайте систему команд для исполнителя «Колдун». Напишите алгоритм приготовления эликсира. |
Тема 6.2 Основные алгоритмические конструкции.
Основные понятия: линейный алгоритм, ветвление, полное и неполное ветвление, циклический алгоритм, цикл с предусловием, цикл с постусловием, цикл с параметром..
Условные обозначения:
 - задания до чтения текста - задания до чтения текста |  - задания во время чтения - задания во время чтения |  - задания после чтения - задания после чтения |
 | Прочитайте текст. Сделайте конспект . |
1. Структура следование.Образуется последовательностью действий, следующих одно за другим:
| Алгоритмический язык | Блок-схема |
| действие 1 действие 2 ... действие n | 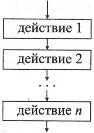 |
Пример.Определить значение переменной c после выполнения фрагмента алгоритма.
| Алгоритмический язык | Блок-схема |
| a:=3 c:=4 c:=a+c/2 |  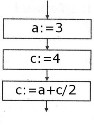 |
Ответ: 5
Пример 2. Составьте блок-схему алгоритма вычисления периметра прямоугольного треугольника по его катетам а и в.
Решение.
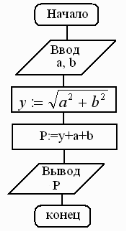
2.Структура ветвление.В зависимости от результата проверки условия («да» или «нет») осуществляет выбор одного из альтернативных путей работы алгоритма. Каждый из путей ведёт к общему выходу, поэтому работа алгоритма будет продолжаться независимо от того, какой путь будет выбран. Структура «ветвление» бывает четырёх видов: «если-то»; «если-то-иначе»; «выбор»; «выбор-иначе».
Структура «если-то».
| Алгоритмический язык | Блок-схема |
| еслиусловие то действия всё | 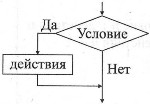 |
Пример 1.Определить значение переменной a после выполнения фрагмента алгоритма при a=5 и a=10.
| Алгоритмический язык | Блок-схема |
| Ввода еслиa>5 то a:=a+20 всё | 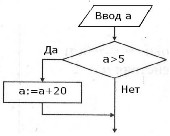 |
Ответ: 5 и 30.
Структура «если-то-иначе».
| Алгоритмический язык | Блок-схема |
| еслиусловие тодействия 1 иначедействия 2 всё | 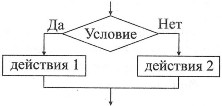 |
Пример 2.Определить значение переменной a после выполнения фрагмента алгоритма при a=5 и a=10.
| Алгоритмический язык | Блок-схема |
| Ввода еслиa>5 то a:=a+20 иначеa:=a*10 всё | 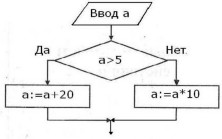 |
Ответ: 50 и 30.
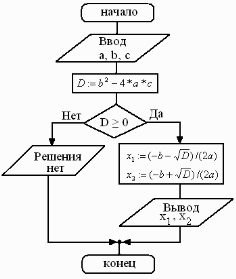
Пример 3. Составьте блок-схему алгоритма решения квадратного уравнения.
Решение.
Структура «выбор».
| Алгоритмический язык | Блок-схема |
| выбор приусловие 1: действия 1 приусловие 2: действия 2 … приусловие n: действия n всё | 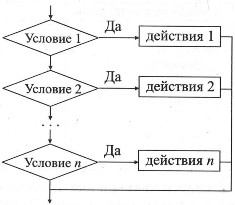 |
Пример 4.Дано целое число в диапазоне 1–7. Составить строку — название дня недели, соответствующее данному числу (1 — «понедельник», 2 — «вторник» и т. д.).
| Алгоритмический язык | Блок-схема |
| выбор приn=1: c:=«понедельник» приn=2: c:=«вторник» приn=3: c:=«среда» приn=4: c:=«четверг» приn=5: c:=«пятница» приn=6: c:=«суббота» приn=7: c:=«воскресенье» всё | 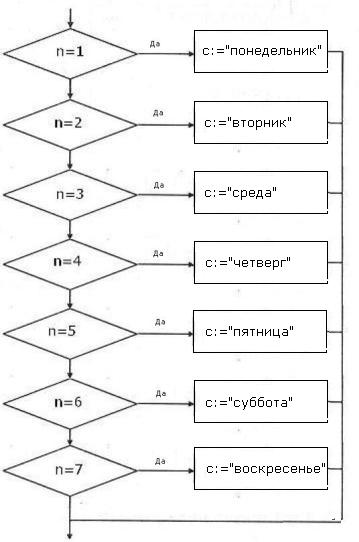 |
Структура «выбор-иначе».
| Алгоритмический язык | Блок-схема |
| выбор приусловие 1: действия 1 приусловие 2: действия 2 … приусловие n: действия n иначедействия n+1 всё | 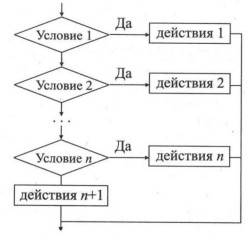 |
Пример 4.Дано целое число n. Составить строку-описание оценки, соответствующей числу n (1 — «плохо», 2 — «двойка», 3 — «тройка», 4 — «хорошо», 5 — «отлично»). Если n не лежит в диапазоне 1–5, то вывести строку «ошибка»
| Алгоритмический язык | Блок-схема |
| выбор приn=1: c:=«плохо» приn=2: c:=«двойка» приn=3: c:=«тройка» приn=4: c:=«хорошо» приn=5: c:=«отлично» иначеc:=«ошибка» всё | 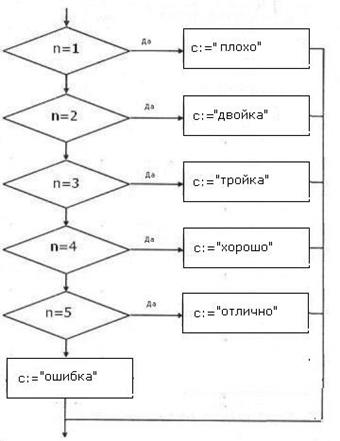 |
3. Структура цикл.Обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла. Циклы бывают трёх видов: с предусловием «пока-делай», с постусловием «делай-пока»,со счётчиком «для».
Цикл с предусловием («пока-делай»). Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова пока.
| Алгоритмический язык | Блок-схема |
| нц покаусловие тело цикла кц | 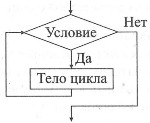 |
Пример 1.
Дано целое число N (> 0). Используя операции деления нацело, найти количество его цифр.
| Алгоритмический язык | Блок-схема |
| K:=0; нц покаN>0 N:=N div 10 K:=K+1 кц | 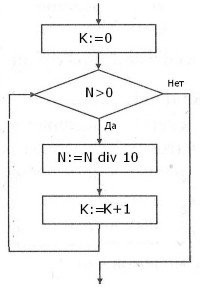 |
Цикл с постусловием («делай-пока»).Предписывает выполнять тело цикла до тех пор, пока не выполняется условие (на Паскале until), записанное после слова пока.В отличие от цикла,«пока-делай» тело цикла выполняется хотя бы один раз.
| Алгоритмический язык | Блок-схема |
| нц тело цикла покаусловие кц | 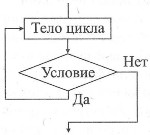 |
Пример 2.
Дано целое число N (> 1). Определить наименьшее из целых чисел K, для которых сумма S= 1 + 2 + … + K будет больше N.
| Алгоритмический язык | Блок-схема |
| S:=0; K:=0 нц K:=K+1 S:=S+K покаS>N кц | 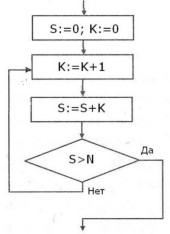 |
Цикл со счетчиком («для»). Предписывает выполнять тело цикла для всех значений переменной (параметр цикла) в заданном диапазоне.
| Алгоритмический язык | Блок-схема |
| нц для iотkдоm тело цикла кц | 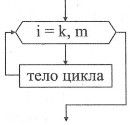 |
Пример 3.Даны два целых числа A и B (A < B). Найти сумму S всех целых чисел от A до B включительно.
| Алгоритмический язык | Блок-схема |
| S:=0 нц для iотAдоB S:=S+i кц | 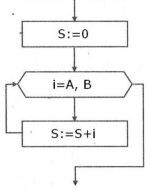 |
Пример 4. Составить блок-схему алгоритма вычисления произведения элементов заданной матрицы A(10,10), расположенных на пересечении четных строк и четных столбцов.
| Алгоритмический язык | Блок-схема |
| i:=2; P:=1 нц пока i <=10 j:=2 нц пока j<=10 P:=P*aij j:=j+2 кц i:=i+2 кц | 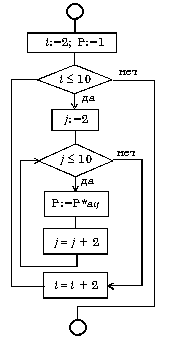 |
 | Выполните задания: 1. Даны длины сторон треугольника A, B, C. Найти площадь треугольника S. Составьте блок-схему алгоритма решения поставленной задачи. 2. Даны координаты вершин треугольника АВС. Найти его площадь. Составьте блок-схему алгоритма решения поставленной задачи. 3. В квадратной комнате шириной A и высотой B есть окно и дверь с размерами C на D и M на N соответственно. Вычислите площадь стен для оклеивания их обоями. Составьте блок-схему алгоритма решения поставленной задачи. 4. Вычислить путь, пройденный лодкой, если ее скорость в стоячей воде v км/ч, скорость течения реки v1 км/ч, время движения по озеру t1 ч, а против течения реки – t2 ч. Составьте блок-схему алгоритма решения поставленной задачи. 5. Дана блок-схема алгоритма: 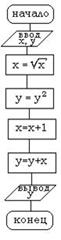 Определить результат выполнения алгоритма при определённых значениях исходных данных, например, при x=16 и y=2. 6. Что вычисляется по данному алгоритму: Определить результат выполнения алгоритма при определённых значениях исходных данных, например, при x=16 и y=2. 6. Что вычисляется по данному алгоритму: 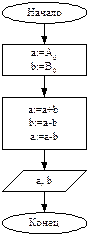 а) Ao + Bo = a + b; б) Ao + Bo = a - b; в) Ao + Bo = - a + b; г) Ao + Bo = - a - b. 7. Дана блок-схема алгоритма: а) Ao + Bo = a + b; б) Ao + Bo = a - b; в) Ao + Bo = - a + b; г) Ao + Bo = - a - b. 7. Дана блок-схема алгоритма: 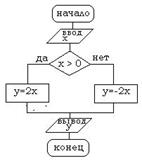 Определить результат выполнения алгоритма при определённых значениях исходных данных, например, при x = -6. 8. Дана блок-схема алгоритма: Определить результат выполнения алгоритма при определённых значениях исходных данных, например, при x = -6. 8. Дана блок-схема алгоритма: 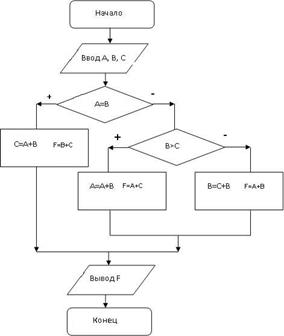 Определить результат выполнения алгоритма при определённых значениях исходных данных, например, при A=7; B=8; C=9. 9. Вычисленное по блок-схеме значение переменной S равно 1. 6; 2. 8; 3. 10; 4. 12. Блок-схема алгоритма: Определить результат выполнения алгоритма при определённых значениях исходных данных, например, при A=7; B=8; C=9. 9. Вычисленное по блок-схеме значение переменной S равно 1. 6; 2. 8; 3. 10; 4. 12. Блок-схема алгоритма:  10. Составьте блок-схему алгоритма, упорядочивающего значения двух переменных X и Y по возрастанию. 11. Составьте блок-схему алгоритма нахождения наибольшего значения среди трех величин: А, В, С. 12. Составьте блок-схему алгоритма вычисления значения функции 10. Составьте блок-схему алгоритма, упорядочивающего значения двух переменных X и Y по возрастанию. 11. Составьте блок-схему алгоритма нахождения наибольшего значения среди трех величин: А, В, С. 12. Составьте блок-схему алгоритма вычисления значения функции 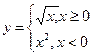 13. Составьте блок-схему алгоритма определяющего, является ли треугольник с заданными сторонами а, в и с равнобедренным. 14. Составьте блок-схему алгоритма определяющего, существует ли треугольник с заданными сторонами а, в и с. 15. Дана блок-схема алгоритма: 13. Составьте блок-схему алгоритма определяющего, является ли треугольник с заданными сторонами а, в и с равнобедренным. 14. Составьте блок-схему алгоритма определяющего, существует ли треугольник с заданными сторонами а, в и с. 15. Дана блок-схема алгоритма:  Определить результат выполнения алгоритма при определённых значениях исходных данных, например, при n=4. 16. Дана блок-схема: Определить результат выполнения алгоритма при определённых значениях исходных данных, например, при n=4. 16. Дана блок-схема: 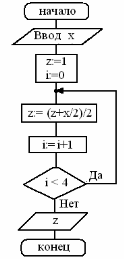 Какое значение будет иметь z на выходе, если x=2? 17. Вычисленное по блок-схеме значение переменной K для входных данных 2, 11, 3 равно а) 1; б) 2; в) 4; г) 8. Блок-схема алгоритма: Какое значение будет иметь z на выходе, если x=2? 17. Вычисленное по блок-схеме значение переменной K для входных данных 2, 11, 3 равно а) 1; б) 2; в) 4; г) 8. Блок-схема алгоритма: 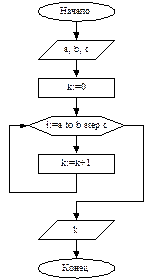 18. Что вычисляется по данному алгоритму: 18. Что вычисляется по данному алгоритму: 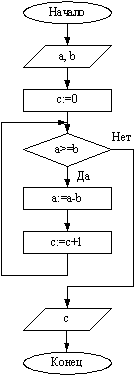 а) результат целочисленного деления b на a; б) остаток от деления a на b; в) результат целочисленного деления a на b; г) остаток от деления b на a. 19. Что вычисляется по данному алгоритму: а) результат целочисленного деления b на a; б) остаток от деления a на b; в) результат целочисленного деления a на b; г) остаток от деления b на a. 19. Что вычисляется по данному алгоритму: 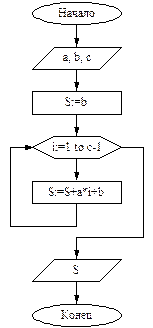 а) сумма первых С членов арифметической прогрессии с первым членом равным А и разностью В; б) сумма первых С членов арифметической прогрессии с первым членом равным В и разностью А; в) сумма первых А членов арифметической прогрессии с первым членом равным В и разностью С; г) сумма первых В членов арифметической прогрессии с первым членом равным А и разностью С? 20. Составить блок-схему алгоритма вычисления функции yk = sin (kx) + cos (k/x), k = 1, 2, ..., 50 Составить блок-схему алгоритма вычисления функции y=a3/(a2+x2) при x, изменяющимся от 0 до 3 с шагом 0,1. а) сумма первых С членов арифметической прогрессии с первым членом равным А и разностью В; б) сумма первых С членов арифметической прогрессии с первым членом равным В и разностью А; в) сумма первых А членов арифметической прогрессии с первым членом равным В и разностью С; г) сумма первых В членов арифметической прогрессии с первым членом равным А и разностью С? 20. Составить блок-схему алгоритма вычисления функции yk = sin (kx) + cos (k/x), k = 1, 2, ..., 50 Составить блок-схему алгоритма вычисления функции y=a3/(a2+x2) при x, изменяющимся от 0 до 3 с шагом 0,1. |
Учебное издание
СПИРИНА Татьяна Венедиктовна, ТРОИЦКАЯ Елена Анатольевна
МАТЕМАТИКА И ИНФОРМАТИКА
Учебное пособие в 2 частях
Часть 2
«Информатика»
[1] Даймонд состоит из семи строк:
первая и седьмая строки – существительные-антонимы;
вторая строка – прилагательное, описывающее первое существительное;
третья строка – три глагола, относящиеся к первому существительному;
четвертая строка – четыре существительных, два из них относятся к первому существительному, два других – ко второму существительному;
пятая строка – три глагола, относящиеся ко второму существительному;
шестая строка – два прилагательных, описывающих второе существительное.
Пример:
День;
Яркий, радостный;
Сияет, обогревает, обнадеживает;
Рассвет, солнце, тени, закон;
Охлаждает, настораживает, приближается;
Загадочная, темная;
Ночь.