Показатели безотказности невосстанавливаемых систем

В качестве случайной величины T примем наработку до отказа (единственного для систем данного класса). Считаем, что нам известна функция распределения F(t) , которая в данном случае будет называться функцией вероятности отказа Q ( t ), т.е.: F(t)= Q ( t ) – ф-я вер-ти отказа, f(t)=f_н(t)- - плотность распред.нараб.отказа.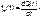

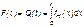
Важнейшим количественным показателем безотказности служит функция вероятности безотказной работы в течение заданного времени t:

.

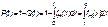Q(t)=1-Р(t).

Плотность распределения вероятностей как показатель безотказности невосстанавливаемых систем принимает смысл плотности распределения наработки на отказ f_H(t), а интенсивность b(t) принимает смысл функции интенсивности отказов l(t):

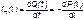
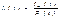
Между функциями P(t) и l(t) существует взаимосвязь:

f_н(t) = . , , ,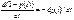

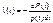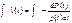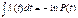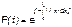
Взаимосвязь между функциями f_H(t) и l(t) можно определить из соотношения:

.

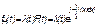Если одна из четырех функций известна, то остальные три можно вычислить по формулам, приведенным в таблице.

Удобный и наглядный физический смысл имеет показатель "средняя наработка на отказ", который равен математическому ожиданию времени исправной работы до первого отказа:

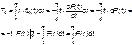
Свойства функции безотказной работы P(t):

1.При t=0, P(t)=1 , т.е. в нулевой момент времени система будет работоспособна.

2. P(t) — монотонно убывающая функция во времени.

3.При t→∞, P(t) → 0.

7 На практике часто требуется определить показатели безотказности при том условии, что элемент, проработавший время t₁, будет безотказно работать в течение промежутка времени от t₁ до t₂ (t₂>t₁). В этом случае основные показатели находятся как условные вероятности. Условная вероятность безотказной работы в течение наработки t = t₂ - t₁ (рис. 1.7) при условии, что система безотказно проработала от 0 до t₁, равна:

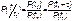
Условная вероятность отказа равна:

.

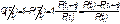Условная интенсивность отказа равна:

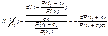
Условная наработка на отказ равна:

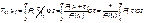
8 Теперь перейдем к рассмотрению статистических оценок показателей безотказности, которые в литературе обозначаются либо символом ^ либо *. Пусть на испытания было поставлено No систем, которые с течением времени отказывали, что модно представить временной диаграммой (No - количество изделий, n(t) - количество отказавших изделий за время t):

Показатели безотказности можно оценивать приближенно по статистическим данным. Рассмотрим формулы для определения статистических значений показателей безотказности. Статистическая оценка вероятности отказа:

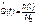
Статистическая оценка вероятности безотказной работы:

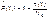
Статистическая оценка плотности распределения наработки на отказ:

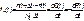
Статистическая оценка интенсивности отказов:

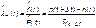
где .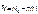

Статистическая оценка средней наработки на отказ находится по формуле:

,

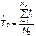где t_i — наработка на отказ i-й системы.