Примеры тождественно истинных формул высказываний

· Закон тождества. «Всякое высказывание является логическим следованием себя самого»

x->x

Доказательство сводится к построению таблиц истинности

x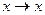

· Закон противоречия. «Для всякого высказывания неверно, что истинно и высказывание х и его отрицание.

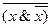
Доказательство сводится к построению таблиц истинности

x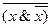

· Закон исключенного третьего. «Для каждого высказывания х истинно или само высказывание, или его отрицание»

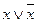
Доказательство сводится к построению таблиц истинности

x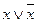

· Закон двойного отрицания. Отрицание от любого высказывания равносильно самому высказыванию.

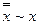
· Добавление антцедента (истина из чего угодно). Если х – истина, то для любого у истинно, что y->x.

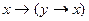
· Из ложного что угодно.

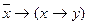
· Modus ponens. Если x->y – истинно и x – истинно, то согласно закону mp можно заключить, что истинно у.

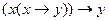
Этот тип заключения очень часто используется при математических доказательствах.

Пример.

1. Все простые числа, большие 2 – нечетны.

2. 7 – простое число.

3. Следовательно, 7- нечетное число.

Здесь применяются 2 закона. Первый закон – закон заключения от общего к частному будет рассмотрен в логике предикатов.

На основании этого закона преобразуется первая посылка заключения: Для всех х, если х – простое число большее 2, то х – нечетно. Согласно заключению от общего к частному высказывание если 7 – простое число большее 2, то 7 – нечетно – истинно. (А)

7 – нечетно (В)

A->B – Истинно

А – истинно

Применяем mp, следовательно, высказывание 7-нечетно – истинно.

· Modus tollens

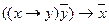
Или

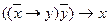
Этот закон применяется при доказательствах от противного. Он является двойственным к mp.

· Закон силлогизма

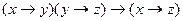
Этот закон позволяет строить сколь угодно длинные цепочки рассуждений.

Формальные теории

Рассмотрим один из методов получения всех тождественно истинных формул логики высказываний. До сих пор мы рассматривали формулы как выражения для булевых функций. Теперь мы будем рассматривать формулы как последовательности символов, построенные по определенным правилам. Для этого нам сначала надо задать алфавит (латинские буквы, знаки логических операций и скобки). Затем определим понятие слова. Слово – конечная последовательность символов.

Формула – это

1) любая переменная (x,y,z,…)

2) Если слова A и B – формулы, то слова 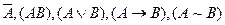и т. д. – формулы.

Свойство формулы: Можно описать процедуру, которая устанавливает, является слово формулой или нет.

Для преобразования формул применяются правила, которые называются правилами вывода.

1. Правило подстановки.

2. правило mp.

Таким образом:

Формальная теория 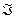- это

1. Множество символов, образующих алфавит А.

2. Множество слов в этом алфавите, которые называются формулами ( ).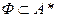

3. Подмножество формул, которые называются аксиомами( ).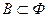

4. Множество отношений между формулами, которые называются правилами вывода (R).

Алфавит может быть конечным или бесконечным. Алфавит и множество формул (А и Ф) образуют сигнатуру теории. Множество аксиом (B) также может быть конечным или бесконечным. Если множество аксиом бесконечно, то оно задается с помощью конечного множества схем аксиом и правил порождения конкретных аксиом из схем аксиом. Аксиомы делятся на два вида: логические (общие для целого класса формальных теорий) и нелогические (собственные) аксиомы, которые определяют специфику и содержание конкретной теории.

Множество правил вывода R – конечно.

Выводимость.

Пусть F₁,F₂,….F_n,G – формулы теории 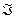(Ф). Применяя к ним правила вывода R можно получить некоторую совокупность формул Ф1, такую, что 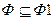. Про формулы из Ф1 можно сказать, что они выводятся из Ф за один шаг. Далее можно рассматривать множество формул Ф2, выводимых из Ф1 за один шаг, т. е. из Ф они выводятся за два шага , и т. д. Некоторая формула А будет считаться выводимой из Ф, если она выводима из Ф за конечное множество шагов, т. е. принадлежит множеству Фm.

Примеры.

1. Пусть Ф=х1. Тогда x1{…}=A, т. е. с помощью правила подстановки можно получить любую однобуквенную формулу. Вывод: х,А., т. е. если из некоторого заданного множества формул выводима однобуквенная формула хi, то из этого множества выводимы все формулы.

2. Пусть Ф=(x1->x2). Тогда (x1->x2){( x1->x2)//x1}=( (x1->x2)->x2). Следовательно из Ф выводима формула ( (x1->x2)->x2) и сама формула (x1->x2). Применим к этим двум формулам правило mp. Получим формулу х2. Если A произвольная формула, то мы можем получить ее из х2 по правилу подстановки.

Вывод: Если все формулы некоторого множества Ф’ выводимы из множества Ф, а А выводима из Ф’, то А выводима из Ф

3. Пусть Ф={A, 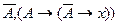}. Тогда из Ф выводима любая формула. Применяя mp к формулам , 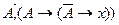получаем формулу 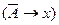.Еще раз применим mp к 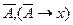, получим х. Следовательно, мы можем вывести любую формулу. Вывод: Если из какой-то системы формул можно вывести А и 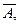то такая система формул называется противоречивой, из нее выводится любая формула.

Выводом формулы G из формул F₁,F₂,….F_n в формальной теории 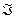называется такая последовательность формул E₁,E₂,….E_k, что E_k=G, а любая формула E_i (i<k) является либо аксиомой, либо исходной формулой, либо непосредственно выводима из ранее полученных формул.

Если в теории 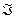существует вывод G из формул F₁,F₂,….F_n, то это записывают следующим образом:

F₁,F₂,….F_n 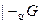, где F₁,F₂,….F_n – гипотезы.

Если 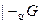, то G – теорема (т. е. теорема – это формула, выводимая из аксиом без гипотез).

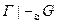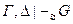Если , то , где 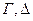- любые множества формул (при добавлении лишних гипотез выводимость сохраняется).