Нормальное распределение. Нормальное распределение или распределение Гаусса является наиболее универсальным, удобным и широко применяемым
Нормальное распределение или распределение Гаусса является наиболее универсальным, удобным и широко применяемым. Нормальное распределение случайной величины возникает всякий раз, когда случайная величина зависит от большого числа однородных по своему влиянию случайных факторов, причем влияние каждого из этих факторов по сравнению с совокупностью всех остальных незначительно. Это условие характерно для времени возникновения отказа, вызванного старением, т.е. этот закон используется для оценки надежности изделий при наличии постепенных (износовых) отказов. Нормальный закон применяется также при малых разбросах значениях скорости изнашивания элементов и при симметричных законах распределения, когда можно подобрать преобразование, позволяющее перейти от этого закона к логарифмически нормальному распределению.
Для нормального закона распределения:
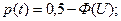 (1.11)
(1.11)
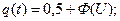 (1.12)
(1.12)
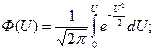 (1.13)
(1.13)
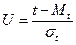 ; (1.14)
; (1.14)
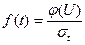 ; (1.15)
; (1.15)
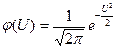 ; (1.16)
; (1.16)
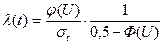 , (1.17)
, (1.17)
где 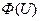 – нормированная функция Лапласа, обладающая – свойствами:
– нормированная функция Лапласа, обладающая – свойствами:
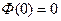 ,
, 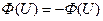 ,
, 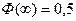 .
.
Монотонное возрастание интенсивности отказов с течением времени – характерный признак нормального распределения. Нормальное распределение существенно отличается от экспоненциального. Началом отсчета времени 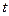 служит начало эксплуатации объекта, т.е. момент, когда начинается процесс износа и старения, а началом отсчета – момент времени, когда установлено, что изделие исправно (этот момент может быть расположен в любой точке на оси времени).
служит начало эксплуатации объекта, т.е. момент, когда начинается процесс износа и старения, а началом отсчета – момент времени, когда установлено, что изделие исправно (этот момент может быть расположен в любой точке на оси времени).
При нормальном распределении наработка до отказа 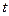 как случайная величина должна принимать должна принимать значения в пределах от
как случайная величина должна принимать должна принимать значения в пределах от 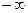 до
до 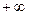 , но так как наработка не может быть величиной отрицательной, то нормальный закон распределения в классическом виде не может быть применен. Распределение может быть лишь усеченным нормальным (рис. 1.11), для которого справедлива формула, показывающая связь между ни и обычной формой закона:
, но так как наработка не может быть величиной отрицательной, то нормальный закон распределения в классическом виде не может быть применен. Распределение может быть лишь усеченным нормальным (рис. 1.11), для которого справедлива формула, показывающая связь между ни и обычной формой закона:
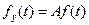 ,
,
где 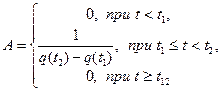 – нормирующий множитель;
– нормирующий множитель;
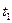 и
и 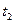 – границы интервала действия закона.
– границы интервала действия закона.
Так как для наработки справедливо 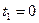 ,
, 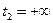 , в этом случае
, в этом случае
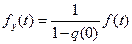 , (1.18)
, (1.18)
причем значение интегрального закона 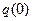 определяется для стандартной, а не для усеченной формы.
определяется для стандартной, а не для усеченной формы.
Принято также считать без серьезного ущерба для точности, что при отношении средней наработки к ее среднеквадратичному отклонению 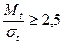 нормирующий множитель
нормирующий множитель 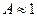 .
.
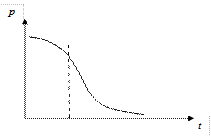 а) а) | 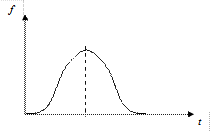 б) б) | 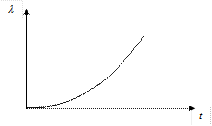 в) в) |
Рисунок 1.11 – Типичные зависимости характеристик надежности
для усеченного нормального распределения
