Показатели безотказности восстанавливаемых систем

ti — i-ая наработка на отказ.

ti — i-ое время восстановления после i-ого отказа

Случайную величину длительности безотказной работы между соседними периодами восстановления системы можно характеризовать функцией распределения длительности безотказной работы между окончанием восстановления после (i-1)-го отказа и моментом наступления i-го отказа Fi(t). Тогда показатель Qi(t) = Fi(t) будет означать вероятность наступления отказа системы за промежуток времени t после окончания (i-1)-го восстановления. Вероятность безотказной работы с момента окончания (i-1)-го восстановления за период t:

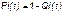
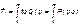
Средняя наработка на отказ за интервал времени от момента окончания (i-1)-го восстановления до наступления i-го отказа: T_oi

Перечисленные показатели можно назвать локальными. Они характеризуют безотказность в интервалах времени между двумя соседними отказами. Частным случаем локальных показателей безотказности восстанавливаемых систем будут показатели безотказности невосстанавливаемых систем, если рассматривать свойства безотказности до первого отказа 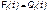; ; 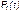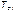и т.д.

Для общего случая, который учитывает все отказы за интервал времени t, используются общие показатели безотказности, в частности ведущая функция потока отказов W(t) (математическое ожидание случайного числа отказов за время t):

,

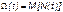где М – математическое ожидание;

N(t) – случайное число отказов.

Следующий общий показатель безотказности - параметр потока отказов (среднее значение количества отказов в единицу времени за рассматриваемый интервал времени - имеет вид

.

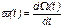Справедливо обратное соотношение

.

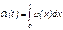Наглядной характеристикой восстанавливаемых систем является среднее значение параметра потока отказов за рассматриваемую наработку T_P:

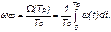
Среднюю наработку между отказами восстанавливаемого изделия характеризует показатель Т:

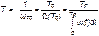
Предел параметра потока отказов

.

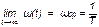Показатель w(t) связан с показателями невосстанавливаемых изделий f(t) и l(t) неравенством

.

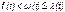Если случайные величины наработки между отказами одинаково распределены и независимы (одинаковые законы распределения случайной величины наработки между отказами), т.е. F1(t) = F2(t) = … = Fk(t), то w(t) связан с плотностью распределения наработки между отказами f(t) уравнением возобновления

.

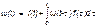В некоторых случаях удобно искать решение преобразование Лапласа:

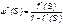
где

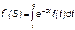
Если функция распределения наработки между отказами подчиняется экспоненциальному закону распределения, то расчет значительно упрощается.

Показатели сохраняемости

Определение свойств сохраняемости аналогично определению свойств безотказности с тем лишь различием, что они относятся к разным условиям: свойство безотказности характеризует рабочие эксплуатационные условия, а свойство сохраняемости – нерабочие условия (хранение и транспортировка). Показатели сохраняемости аналогичны показателям безотказности. Однако вычислять их нужно не через функции f_н(t) и Q(t), а через законы распределения длительности безотказного хранения f_хр(t) и F_хр(t).

Срок сохраняемости – календарная продолжительность хранения или транспортировки изделия, в течение и после которой сохраняются значения показателей безотказности, долговечности и ремонтопригодности в установленных пределах.

Из всего множества показателей сохраняемости наиболее часто в технической документации используют только два: средний срок сохраняемости и гамма-процентный срок сохраняемости.

Средний срок сохраняемости — математическое ожидание случайной величины хранения до отказа:

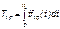
Гамма-процентный срок сохраняемости — срок сохраняемости, который достигается объектом с вероятностью g выраженной в процентах T_хрg:

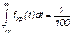
Рекомендуются значения g = 90; 95 и 98%. Кроме того, применяют еще и медианный срок сохраняемости при g = 50% T_хрμ: