Основные термины и определения

Понятие нечеткого множества - эта попытка математической формализации нечеткой информации для построения математических моделей. В основе этого понятия лежит представление о том, что составляющие данное множество элементы, обладающие общим свойством, могут обладать этим свойством в различной степени и, следовательно принадлежать к данному множеству с различной степенью. При таком подходе высказывания типа “такой-то элемент принадлежит данному множеству” теряют смысл, поскольку необходимо указать “насколько сильно” или с какой степенью конкретный элемент удовлетворяет свойствам данного множества.

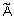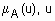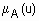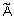Определение 1.Нечетким множеством (fuzzy set) на универсальном множестве U называется совокупность пар ( ), где - степень принадлежности элемента к нечеткому множеству . Степень принадлежности - это число из диапазона [0, 1]. Чем выше степень принадлежности, тем в большей мерой элемент универсального множества соответствует свойствам нечеткого множества.

Определение 2.Функцией принадлежности(membership function) называется функция, которая позволяет вычислить степень принадлежности произвольного элемента универсального множества к нечеткому множеству.

Если универсальное множество состоит из конечного количества элементов 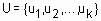, тогда нечеткое множество 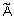записывается в виде 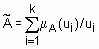. В случае непрерывного множества U используют такое обозначение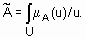

Примечание: знак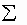и и 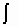в этих формулах означают совокупность пар 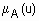и u.

Пример 1.Представить в виде нечеткого множества понятие “мужчина среднего роста”.

Решение: 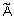= 0/155+0.1/160 + 0.3/165 + 0.8/170 +1/175 +1/180 + 0.5/185 +0/180.

Определение 3.Лингвистической переменной (linguistic variable) называется переменная, значениями которой могут быть слова или словосочетания некоторого естественного или искусственного языка.

Определение 4.Терм–множеством (term set) называется множество всех возможных значений лингвистической переменной.

Определение 5.Термом (term) называется любой элемент терм–множества. В теории нечетких множеств терм формализуется нечетким множеством с помощью функции принадлежности.

Пример 2.Рассмотрим переменную “скорость автомобиля”, которая оценивается по шкале “низкая", "средняя", "высокая” и “очень высокая".

В этом примере лингвистической переменной является “скорость автомобиля”, термами - лингвистические оценки “низкая", "средняя", "высокая” и “очень высокая”, которые и составляют терм–множество.

Определение 6.Дефаззификацией (defuzzification) называется процедура преобразования нечеткого множества в четкое число.

В теории нечетких множеств процедура дефаззификации аналогична нахождения характеристик положения (математического ожидания, моды, медианы) случайных величин в теории вероятности. Простейшим способом выполнения процедуры дефаззификации является выбор четкого числа, соответствующего максимуму функции принадлежности. Однако пригодность этого способа ограничивается лишь одноэкстремальными функциями принадлежности. Для многоэкстремальных функций принадлежности в Fuzzy Logic Toolbox запрограммированы такие методы дефаззификации:

Centroid - центр тяжести;

Bisector - медиана;

LOM (Largest Of Maximums) - наибольший из максимумов;

SOM (Smallest Of Maximums) - наименьший из максимумов;

Mom (Mean Of Maximums) - центр максимумов.

Определение 7.Дефаззификация нечеткого множества 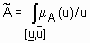по методу центра тяжести осуществляется по формуле .

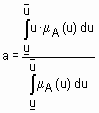Физическим аналогом этой формулы является нахождение центра тяжести плоской фигуры, ограниченной осями координат и графиком функции принадлежности нечеткого множества. В случае дискретного универсального множества дефаззификация нечеткого множества 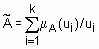по методу центра тяжести осуществляется по формуле .

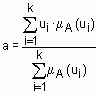Определение 8.Дефаззификация нечеткого множества 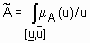по методу медианы состоит в нахождении такого числа a, что .

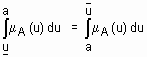Геометрической интерпретацией метода медианы является нахождения такой точки на оси абцисс, что перпендикуляр, восстановленный в этой точке, делит площадь под кривой функции принадлежности на две равные части. В случае дискретного универсального множества дефаззификация нечеткого множества 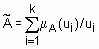по методу медианы осуществляется по формуле .

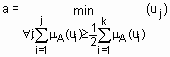Определение 9.Дефаззификация нечеткого множества 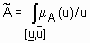по методу центра максимумов осуществляется по формуле:

,

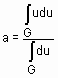где G – множество всех элементов из интервала 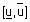, имеющих максимальную степень принадлежности нечеткому множеству .

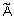В методе центра максимумов находится среднее арифметическое элементов универсального множества, имеющих максимальные степени принадлежностей. Если множество таких элементов конечно, то формула из определения 9 упрощается к следующему виду:

,

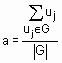где 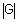- мощность множества G.

В дискретном случае дефаззификация по методам наибольшего из максимумов и наименьшего из максимумов осуществляется по формулам 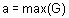и , соответственно. Из последних трех формулы видно, что если функция принадлежности имеет только один максимум, то его координата и является четким аналогом нечеткого множества.

Пример 3. Провести дефаззификацию нечеткого множества “мужчина среднего роста” из примера 1 по методу центра тяжести.

Решение: Применяя формулу из определения 7, получаем:

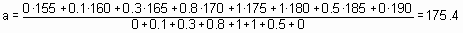
Определение 10.Нечеткой базой знаний (fuzzy knowledge base) о влиянии факторов 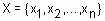на значение параметра y называется совокупность логических высказываний типа:

ЕСЛИ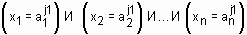

ИЛИ …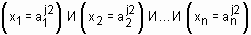

ИЛИ ,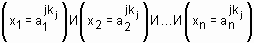

ТО 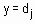, для всех ,

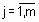где 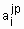- нечеткий терм, которым оценивается переменная 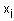в строчке с номером jp ( );

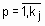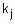- количество строчек-конъюнкций, в которых выход y оценивается нечетким термом , ;

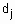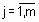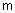- количество термов, используемых для лингвистической оценки выходного параметра y.

С помощью операций 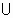(ИЛИ) и 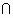(И) нечеткую базу знаний из определения 10 перепишем в более компактном виде:

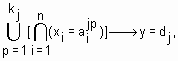
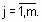(1)

Определение 11.Нечетким логическим выводом (fuzzy logic inference) называется апроксимация зависимости 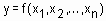с помощью нечеткой базы знаний и операций над нечеткими множествами.

Пусть 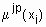- функция принадлежности входа 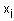нечеткому терму 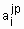, , 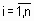, , 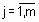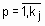т. е. 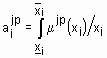; 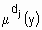- функция принадлежности выхода y нечеткому терму 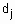, , 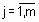т. е. 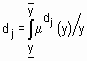. Тогда степень принадлежности конкретного входного вектора 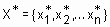нечетким термам 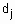из базы знаний (1) определяется следующей системой нечетких логических уравнений:

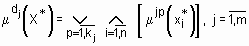, (2)

где 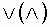- операция максимума (минимума).

Нечеткое множество 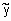, соответствующее входному вектору 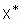, определяется следующим образом:

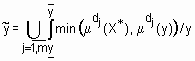, (3)

где 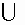- операция объединения нечетких множеств.

Четкое значение выхода y, соответствующее входному вектору 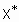определяется в результате деффаззификации нечеткого .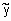