Арифметические вычисления

Язык Пролог не предназначен для программирования задач с большим количеством арифметических операций. Для этого используются процедурные языки программирования. Однако в любую Пролог-систему включаются обычные арифметические операции и функции:

X + Y	Сумма X и Y
X – Y	Разность X и Y
X * Y	Произведение X и Y
X / Y	Деление X на Y
X mod Y	Остаток от деления X на Y
abs(X)	Абсолютная величина числа X
sqrt(X)	Квадратный корень из X
random(X)	Случайное число в диапазоне от 0 до 1
random(Int,X)	Случайное целое число в диапазоне от 0 до Int
sin(X)	Синус X
cos(X)	Косинус X
tan(X)	Тангенс X
log(X)	Натуральный логарифм (ln) числа X

Пролог располагает двумя числовыми типами доменов: целыми и действительными числами. Пролог позволяет также сравнивать арифметические выраже­ния, используя отношения:

=, <, <=, >, >=, <>

Для реализации математических действий в Прологе используются предикаты. Следующие примеры демонстрируют их использование.

Пример 1.

Найти среднее арифметическое двух чисел.

PREDICATES

Sr (real, real, real)

CLAUSES

Sr (A, B, S):- S = (A+B)/2.

GOAL

Sr (8, 12, S), write (S).

Результат:

Пример 2.

Определить является ли натуральное число четным или нечетным

PREDICATES

Chet (integer)

CLAUSES

Chet (A): - A mod 2 =0, write (A, ‘- четное’); Write (A, ‘- не четное’).

GOAL

Chet (18).

Результат:

18 – четное

Рекурсия

Рекурсия – это второе средство для организации повторяющихся действий в ПРОЛОГе. Рекурсивная процедура – это процедура, вызывающая сама себя до тех пор, пока не будет соблюдено некоторое условие, которое остановит рекурсию. Такое условие называют граничным. Рекурсия – хороший способ для решения задач, содержащих в себе подзадачу такого же типа. Рекурсивное правило всегда состоит по крайней мере из двух частей, одна из которых является нерекурсивной. Она определяет граничное условие.

Рассмотрим рекурсивное определение правила на примере правила predok

1. X является предком Z, если X - родитель Z

predok(X, Z):-roditel(X, Z)

2. X – предок для Z, если найдется такой Y, для которого X является родителем и Y является предком Z .

Predok (X,Z) :- roditel (X,Y), predok (Y,Z).

Первая часть этого правила нерекурсивная, она определяет условие завершения рекурсии. Поиск прекратится, как только будет найден ближайший предок - родитель.

Программа:

DOMAINS

name = string

PREDICATES

roditel (name, name)

predok (name, name)

CLAUSES

roditel (коля, оля).

roditel (оля, маша).

predok (X, Z):- roditel (X, Z).

predok (X, Z):- roditel (X,Y), predok (Y, Z).

GOAL

predok (коля, маша).

Результат:

Yes

Пример. Рекурсивное вычисление факториала

Задача нахождения значения факториала n! сводится к нахождению значения факториала (n-1)! и умножения найденного значения на n.

Правило для вычисления факториала:

1. 0! = 1

fact (0, 1):- !. % нерекурсивная часть правила

2. N! = (N-1)!*N.

fact (N, FN):- M=N–1, % рекурсивная часть правила

fact (M, FM), FN=FM*N.

Программа:

PREDICATES

fact (integer, integer)

CLAUSES

fact (0, 1):- !.

fact (N, FactN):- M=N–1, fact (M, FactM), FactN=FactM*N.

GOAL

fact (3, FN), write (“3!=”, FN).

Результат работы программы:

3!=6

Для наглядного представления нахождения решения удобно использовать дерево целей:

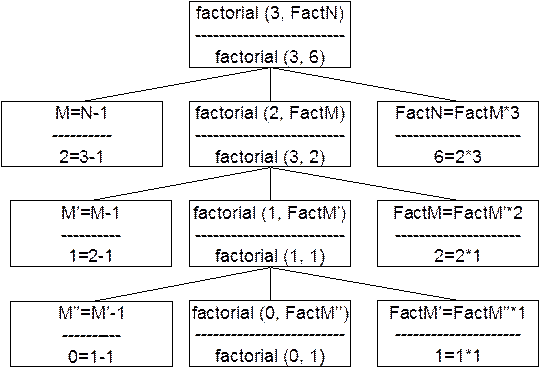
рис.3 Целевое дерево вычисления факториала

Списки

Список – это объект, который содержит конечное число других объектов. Список в ПРОЛОГе можно приблизительно сравнить с массивами в других языках, но для списков нет необходимости заранее объявлять размерность.

Список в ПРОЛОГе заключается в квадратные скобки и элементы списка разделяются запятыми. Список, который не содержит ни одного элемента, называется пустым списком.

Примеры списков:

список, элементами которого являются целые числа: [1, 2, 3]

список, элементами которого являются строки: [“One”, “Two”, “Three”]

пустой список: []

Элементами списка могут быть списки: [[-1,3,5],[6,4,2,8]]

Чтобы использовать в ПРОЛОГ-программе списки, необходимо в разделе DOMAINS описать тип домена в формате.

<имя домена> = <тип элементов>*

Например,

DOMAINS

list = <integer>*

Список является рекурсивным объектом. Он состоит из головы (первого элемента списка) и хвоста (все последующие элемента). Хвост также является списком.

Например, [A, B, C] - список , у которого А – голова, [B,C] - хвост

В ПРОЛОГе имеется операция “|”, которая позволяет делить список на голову и хвост.

[A, B, C] = [A | [B, C] ] = [A | [B | [C] ] ] = [A | [B | [C | [ ] ] ] ]

Пустой список нельзя разделить на голову и хвост. Такая структура позволяет использовать рекурсию для обработки списка.

Пример программы, осуществляющей вывод элементов списка.

DOMAINS

list = integer *

PREDICATES

writelist(list)

CLAUSES

writelist ([]).

writelist ([A | Z]) :- write (A), nl, writelist (Z).

GOAL

writelist([10, 20, 30, 40]).

Результат выполнения программы:

В данной программе A – голова списка, Z – его хвост