Оценка случайных погрешностей косвенных измерений

В соответствии с формулой (1.2) результат косвенного измерения находят по данным прямых измерений нескольких величин
(аргументов), связанных известной функциональной зависимостью
с искомым результатом. Так как результаты прямых измерений
аргументов содержат погрешности, результат косвенного измерения также будет содержать погрешность. Поэтому, как и в случае
прямых измерений, стоит задача оценки истинного значения измеряемой величины Q и доверительных границ погрешности результата косвенного измерения.

За результат косвенного измерения принимается величина Q, вычисляемая при подстановке в формулу (1.2) средних арифметических значений аргументов, полученных с помощью формулы (1.17):

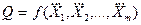, (1.29)

причем свойства оценок 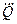и 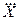аналогичны.

Для оценки СКО 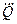метрологическая литература дает формулу:

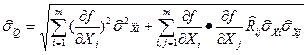. (1.30)

Величина:

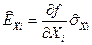. (1.31)

Коэффициент корреляции определяет, как известно, степень статической связи между случайными величинами (в данном случае между погрешностями измерения Xi и Xj). Возможные значения коэффициента корреляции лежат в интервале:

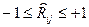. (1.32)

Как видно из (1.32), в процессе обработки результатов наблюдений при косвенных измерениях могут встретиться случай независимых частных погрешностей (Rij=0) и случай зависимых частных погрешностей (Rij≠0). Первый имеет место на практике, когда величины Xi и XJ измеряют с помощью различных СИ, в разное время, измерения проводятся разными операторами и т. д. В этом случае формула (1.30) существенно упрощается и с учетом (1.31) принимает вид

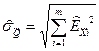. (1.33)

Во втором случае расчет 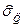должен производиться по общей формуле (1.30). Это имеет место тогда, когда Xi и Xj измеряются одним оператором, с помощью однотипных СИ, при одновременном изменении влияющих величин и т. п. Если Rij>0 (положительная корреляция), то одна из погрешностей имеет тенденцию возрастать при увеличении другой. Если же Rij<0 (отрицательная корреляция), тенденция будет обратной. Это хорошо видно из графиков, изображенных на рис. 1.2, а, б, которые могут быть использованы для экспериментального определения наличия и характера корреляции (график на рис. 1.2, в свидетельствует об отсутствии корреляции). Количественная оценка Rij; может производиться по формуле:

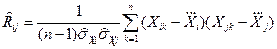, (1.34)

где n – наименьшее из чисел наблюдений Xik и Xjk.

Рис. 1.2. Графики, иллюстрирующие наличие и характер корреляции между погрешностями измерения аргументов Xi и X,:

а — положительная корреляция; б — отрицательная корреляция; в — корреляция отсутствует.

Так как практическое определение Rij весьма затруднительно, важное значение имеет выделение при суммировании по формуле (1.30) групп частных погрешностей, сильно коррелированных между собой. Для погрешностей внутри групп можно принять Rij= ±1и алгебраически сложить погрешности внутри каждой группы. Полученные таким образом суммарные погрешности групп уже не имеют заметных корреляционных связей и могут складываться по формуле (1.33).

Переходя от точечной к интервальной оценке случайной погрешности результата косвенного измерения, определим доверительные границы ее по формуле, аналогичной (1.22):

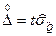. (1.35)

В отношении правил выбора коэффициента Стьюдента необходимо отметить следующее. Если n>ЗО, значение t прямо выбирается из табл. 1.2. Если же n<30, предварительно должно быть определено так называемое «эффективное» число степеней свободы распределения Стьюдента, учитываемое затем при пользовании табл.1.2:

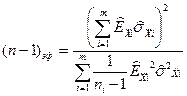, (1.36)

где ni — число наблюдений при прямых измерениях Xi.

В заключение рассмотрим так называемый критерий ничтожных погрешностей. Дело в том, что не все частные погрешности оказывают одинаковое влияние на формирование суммарной погрешности результата косвенного измерения. Некоторые из них могут быть значительно меньше других, а поскольку значение 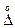все равно должно округляться по правилам ГОСТ 8.011—72 до двух значащих цифр, они не будут оказывать заметного влияния на 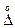. Такие погрешности называются ничтожно малыми (ничтожными). Указанное правило округления позволяет считать какую-то частную погрешность ничтожной, если она изменит соответствующую суммарную погрешность не более чем на 5 %. Рассмотрим на примере оценки 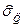по формуле (1.33), как из этого исходного условия может быть окончательно сформулирован критерий ничтожных погрешностей.

В соответствии с исходным условием частная погрешность 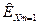может считаться ничтожной, если в формуле (1.33):

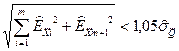
откуда:

,

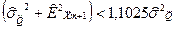т.е окончательно:

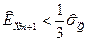. (1.37)

Условие (1.37) и получило название критерия ничтожных погрешностей: если частная погрешность меньше 1/3 соответствующей суммарной погрешности, она может быть исключена из рассмотрения. Как и критерий грубых погрешностей, критерий ничтожных погрешностей имеет важное практическое значение. Он позволяет выявить величины, повышение точности измерения которых существенно уменьшает суммарную погрешность результата измерения, а также случаи, когда точность измерения каких-то величин повышать не имеет смысла.