Модифицированные коды Бергера

Для повышения эффективности обнаружения искажений в информационных векторах S(m,k)-кодов разработан алгоритм преобразования контрольного вектора в слове кода Бергера в контрольный вектор нового (модифицированного) кода (обозначим его как RS(m,k)-код).

Алгоритм. Правила построения модифицированного кода Бергера.

1. Фиксируется модуль .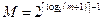

2. Подсчитывается вес информационного вектора r.

3. Число r представляется по модулю M (другими словами, определяется вычет числа r по заданному модулю): .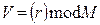

4. Определяется поправочный коэффициент α, равный сумме по модулю два произвольного (но заранее установленного) числа любых информационных разрядов.

5. Формируется число .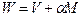

6. Полученное число W представляется в двоичном виде и записывается в контрольный вектор.

Информационные векторы RS(4,3)-кода более равномерно распределены на контрольные группы, чем информационные векторы S(4,3)-кода (табл. 2). RS(4,3)-кода имеет 24 необнаруживаемые ошибки, что в 2,25 раза меньше, чем у S(4,3)-кода. Однако RS(4,3)-код не является оптимальным и имеет коэффициент эффективности ξ=0,6667. В среднем модифицированные коды Бергера обнаруживают примерно в два раза больше искажений в информационных векторах, чем классические коды с суммированием, и более близки к оптимальным (m,k)-кодам.

Таблица 2. RS(4,3)-код

r
Контрольный вектор

В зависимости от формулы вычисления поправочного коэффициента α для данного значения m можно построить 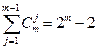модифицированных кодов с суммированием. От этой же формулы зависят и свойства RS(m,k)-кода по обнаружению искажений в информационных векторах. При этом существенным является только количество информационных разрядов в линейной сумме α, но не конкретное положение разрядов в информационном векторе (обозначим число различных информационных разрядов в формуле поправочного коэффициента α как t). Поэтому число модифицированных кодов с суммированием с различными характеристиками по обнаружению искажений в информационных векторах ограничивается не числом сочетаний информационных разрядов в α, а величиной, равной длине информационного вектора. Более того, как показывают исследования, RS(m,k)-коды при заданном значении m обладают симметричными распределениями чисел необнаруживаемых ошибок по всем кратностям относительно величины .

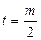Для определения свойств RS(m,k)-кодов по обнаружению ошибок в информационных векторах была составлена компьютерная программа, реализующая алгоритм распределения информационных векторов на контрольные группы и подсчитывающая число необнаруживамых ошибок по кратностям d. C ее помощью были установлены следующие особенности RS(m,k)-кодов:

1. Распределения необнаруживаемых ошибок по кратностям d в RS(m,k)-кодах являются одинаковыми при одинаковом значении t.

2. Всего существует 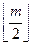разновидностей RS(m,k)-кодов, каждый из которых имеет отличное от других распределение необнаруживаемых ошибок по кратностям d.

3. RS(m,k)-коды с числом информационных разрядов в формуле поправочного коэффициента α равным t и m–t имеют одно и то же распределение необнаруживаемых ошибок.

4. Для RS(m,k)-кодов с M³8 минимальным общим количеством необнаруживаемых ошибок обладает код, в котором для определения α использовалась сумма 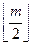информационных разрядов.

5. Минимум необнаруживаемых искажений кратности d=2 имеет модифицированный код, для определения α в котором использовалась сумма 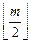информационных разрядов.

6. При малых m в RS(m,k)-кодах доминируют необнаруживаемые ошибки малых кратностей, с увеличением m последовательно приоритет по количеству необнаруживаемых ошибок переходит к ошибкам больших кратностей.

Заключение

В данной статье рассмотрены свойства кодов с суммированием единичных информационных разрядов по обнаружению монотонных ошибок в информационных векторах. Установлено, что возникновение монотонных необнаруживаемых ошибок в модифицированных и модульно модифицированных кодах с суммированием связано с модулем M, по которому вычисляется вес информационного вектора. Результаты данной работы позволяют на практике устанавливать критерии применения кодов с суммированием при организации контроля комбинационных схем, любые одиночные неисправности элементов в которых могут приводить только к монотонным искажениям на выходах.