Логические операции с понятиями

С понятиями — в связи с их количественным и качественным параметрами — можно осуществлять ряд логических операций: 1) обобщение и ограничение, 2) определение, 3) деление, 4) операции с объёмами (классами).

1). Операции обобщения и ограничения понятия осуществляются в связи с непосредственным применением закона обратного отношения между объёмами и содержаниями понятий. Обобщение понятия — логическая операция перехода от понятия с меньшим объёмом, но с большим содержанием (т. е. видового понятия) к понятию с большим объёмом, но с меньшим содержанием (т. е. родовому понятию) за счёт отбрасывания от содержания видового понятия его видообразующего признака. В ходе последовательного проведения операции обобщения может иметь место цепочка последовательного перехода от единичного понятия к всё большим по объёмам понятиям (вплоть до универсального — предельно общего). Естественно, что предельно общее понятие обобщению не подлежит. Ограничение понятия — логическая операция перехода от понятия с большим объёмом, но с меньшим содержанием (т. е. родового понятия) к понятию с меньшим объёмом, но с большим содержанием (т. е. видовому понятию) посредством добавления к содержанию родового понятия видообразующих признаков. Следует учесть: если логической операции обобщения не подлежат универсальные понятия, то к единичным, т. е. содержащим в своём объёме единственный элемент, понятиям не применима логическая операция ограничения понятия.

V Пример

Обобщения понятия. В качестве исходного возьмём единичное понятие «студент группы СО-211 Иванов В.Э.» (А); на следующем шаге, отбросив видообразующий признак «быть Ивановым В.Э.», получим общее понятие «студент группы СО-211» (В); затем — «студент группы СО» (С); далее — «студент» (D); далее — «учащийся» (Е) (результирующая схема — слева).

Ограничения понятия. Сделаем исходным общее понятие «водоём» (А). Добавив видообразуюший признак («быть пресноводным»), получим меньшее по объёму понятие «пресный водоём» (В). Затем — «сточный пресный водоём» (С); далее — «сточный пресный водоём степной части Алтайского края» (D); далее — «река Бурла — сточный пресный водоём северной степной части Алтайского края» (Е) (рис. 8).

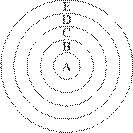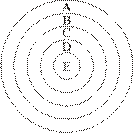Рис. 8

2). Поскольку любое понятие имеет содержание, постольку с ним может быть осуществлена логическая операция раскрытия этого содержания, называемая операцией определения понятия, или дефиницией (от лат. definitio — предел, граница). По сути операции определения понятия в ней участвуют 2-а структурных элемента: 1). Определяемая часть, т.е. понятие, содержание которого требуется раскрыть. Эта часть также называется дефиниендум (от лат. definiendum— определяемое). Для обозначения определяемой части в логике используется символ Dfd. 2). Определяющая часть, т.е. понятие, раскрывающее содержание определяемой части. Для её обозначения используется термин дефиниенс (от лат. definience— определяющее) и соответствующий символ — Dfn. Определяющая часть в определении призвана раскрыть главное в предмете, тем самым выделить этот предмет, отличить его от других предметов, что способствует избеганию смешения понятий и путаницы в рассуждениях и достигается при помощи различных видов определений. Определение подчиняется принципам (законам) формальной логики, следовательно, и закону тождества. В этом аспекте общая структура определения, как соотнесение определяемой и определяющей частей, может быть символически выражена как тождество дефиниендума и дефиниенса: Dfd º Dfn.Основыми видами определений являются: 1) номинальные и реальные определения; 2) явные и, соответственно, неявные определения. 1). Номинальным называется определение, вводящее или новый термин для определения понятия-термина, или краткие имена взамен более сложных описаний предметов. Причём в составе номинальных определений как правило присутствует речевой оборот «называется» и его аналоги. Реальным называет определение, которое (в отличие от определения номинального, т. е. объясняющего значение термина) раскрывает существенные признаки определяемого предмета.

V Пример

Номинальные определения.Определим термин «нестрогая дизъюнкция», введя логический знак, заменяющий этот термин: «Дизъюнкция обозначается знаком «Ú». В свою очередь: «Пантеизм — термин, обозначающий отождествление «бога» со всем существующим в мире в целом». Или: «Словом «пантеизм», происходящим от древнегреческих слов (παν — «всё, всякий» и θεός — «бог, божество»), называется философское учение, отождествляющее мир с Богом».

Реальное определение. «Формальная логика — наука о зако­нах и операциях правильного мышле­ния».

2). Явное определения, т. е. такое, в котором установлено некоторое отношение равенства между дефиниендумом и дефиниенсом; в качестве наиболее распространённого — это так называемое определение через ближайший род и видовое отличие. Это могут быть также и генетические определения, т. е. раскрывающие содержание понятия путём указания на способ образования данного конкретного предмета, выражаемого этим понятием.

V Пример

Определение через ближайший род и видовое отличие. «Квадрат — правильный четырёхугольник или ромб, у которого все углы прямые, или параллелограмм, у которого все стороны и углы равны». Генетическое определение. «Кислоты — это вещества, образующиеся из кислотных остатков и атомов водорода».

Выполняя явное определение, следует соблюдать совокупность правил:

1-е правило: Определение должно быть соразмерным, т. е. объём дефиниендума должен быть равен объёму дефиниенса. В случае несоблюдения данного правила возможны 3-и ошибки: 1). Широкое определение, т. е. когда объём определяющей части оказывается больше объёма дефиниендума. 2). Узкое определение, т. е. когда объём дефиниендума оказывается больше объёма определяющей части. 3). В одном отношении узкое, а в другом — широкое определение.

V Пример

Широкое определение: «Студент – это учащийся». Ошибка в том, что помимо студентов в объёме понятия учащийся имеются и другие элементы (не студенты, например, школьники). В таком случае объём определяемой части меньше объёма определяющей части: Dfd < Dfn.

Узкое определение: «Отношение несовместимости между понятиями – это отношение противоречия». В данном случае упущено то, что к несовместимости понятий относится и отношение противоположности. Следовательно, Dfd > Dfn.

В одном отношении узкое, а в другом — широкое определение: «Древесина — материал для производства мебели». Это определение широкое (Dfd < Dfn) в том отношении, что материалом для производства мебели служат помимо древесины многие другие материалы (металлы, пластик, стекло и т. д.) Это же определение узкое (Dfd > Dfn), поскольку древесина служит не только материалом для изготовления мебели, но и материалом для химической перегонки, сжигания и т. д.

2-е правило: Определение не должно содержать в себе круга, т. е. того случая, когда в определяемой части явно или скрыто уже содержится то, что даётся в определяемой части. Круг возникает, когда Dfd определяется через Dfn, который был определён через Dfd, а также если определяемое понятие даётся через него же само, лишь иначе словесно выраженное, или когда определяемое понятие включается в определяющее понятие в виде его части. В результате несоблюдения данного правила имеют место тавтологии в определении (от греч. ταὐτός — тот же самый и λόγος — слово).

V Пример

Винтовая лестница — это лестница, имеющая форму винта.

3-е правило: Определение должно быть ясным, чётким, т. е. в определении непонятное не должно выражаться непонятным (неясным, двусмысленным). Это правило требует, чтобы смысл и объём понятий, входящих в определяющую часть, был определённым, ясным и тем самым запрещает подмену определений иносказаниями, сравнениями, метафорами и т. д.

V Пример

Философия — служанка богословия или царица наук.

4-е правило: Определение не должно быть отрицательным. Использование отрицания в определении не позволяет раскрыть определяемого понятия, т. к. отрицание указывает на то, чем какой-либо предмет не является, но не сообщает того, что он такое в положительном смысле. Исключением из действия данного правила являются определения, в которых в качестве дефиниендума выступает отрицательно понятие.

V Пример

Проступок — не преступление (ошибка использования отрицания). Без таковой ошибки: «Аморализм — отрицающий моральные устои и общепринятые нормы принцип практической или идейной ориентации чьего-либо поведения».

Раскрывая содержание понятия, кроме явных используют и неявные определения, подставляя на место определяющей части контекст (контекстуальное определение), описание алгоритма построения определяемого предмета (индуктивное определение), набор аксиом (определение через аксиомы). Кроме того, отнюдь не всегда требуется или возможно дать какое-либо определение какому-либо предмету мысли, в таком случае определение понятия часто заменяется приёмами, сходными с данной логической операцией, а именно: 1) описанием, 2) характеристикой, 3) сравнением (различением), 4) указанием посредством примера.

3). Поскольку понятие имеет объём, постольку с общими по объёму понятиями может быть осуществлена логическая операция деления, в познавательных целях распределяющая мыслимые в понятии предметы на отдельные группы, и в частности может быть получена такая разновидность деления понятия, как классификация. Делением понятия называется логическая операция, посредством которой объём исходного понятия (множество) с помощью избранного основания деления распределяется на ряд подмножеств, т. е. это логическая операция, раскрывающая объём понятия. Всякое понятие, повторим ещё раз, имеет содержание, являющееся совокупностью признаков, следовательно, выбрав из этой совокупности определённый признак (подходящий для решения конкретной познавательной задачи деления понятия), мы определяемся с основанием деления. Основание деления — признак, по которому производится операция деления понятия. В ходе операции деления делимое понятие, на основе выбранного из его содержания основания деления, разбивается на члены деления, т. е. соподчинённые понятия (результат деления).

V Пример

В качестве делимого понятия возьмём общее понятие «город»; оно имеет множество различных признаков, например, площадь, количество населения, время основания, географическое положение, государственная принадлежность и прочее. По каждому из этих признаком, взяв его в качестве основания деления, можно выявить, зафиксировать существование различных групп (видов) городов, т. е. получить совокупность членов деления.

Возможны следующие основные виды деления понятия: 1) дихотомическое деление, 2) деление по видообразующему признаку. Дихотомическим (греч. διχοτομαί — рассечение на две части, сечение на два вида) делением является такое, при котором объём делимого понятия (А) делится на два ис­черпывающих его взаимоисключающих множества (В и не-В). Делением по видообразующему признаку называется такое раскрытие объёма делимого понятия, в результате которого выделяются более чем два соподчинённых члена деления.

V Пример

Дихотомическое деление. В содержании понятия «логика» (А) в качестве основания для деления возьмём признак «являться классической». Соответственно, выделим в объёме делимого понятия (А) подмножество тех элементов (В), которые обладают данным признаком, и подмножество тех элементов (не-В), которые не обладают данным признаком. Таким образом, в объёме делимого понятия оказались выявлены два подкласса, соответствующие противоречащим понятиям «классическая логика» (В) и «неклассическая логика» (не-В). Схема данного деления изображена слева.

Деление по видообразующему признаку,Треугольники (А) по признаку (основанию деления) «величина угла» подразделяются на 3-и множества: 1) прямоуголь­ные (В), 3) тупоугольные (С) и 3) остроугольные (D) (рис. 9).

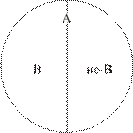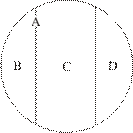Рис.9

Классификация. Имеет место в случае последовательного деления понятия, образующего развёрнутую с относительно устойчивым характером и познавательно значимую систему, в которой её члены подразделёны на подвиды вплоть до одноэлементного понятия. К классификации может приводить как дихотомическое деление понятия, так и деление понятия по видообразующему признаку.

V Пример

По признаку «иметь миллион жителей» дихотомически последовательно поделим понятие «сибирский город» (А). На 1-ом шаге получим: «сибирские города-миллионники» (В) и «сибирские города-немиллионники» (не-В). На 2-ом шаге по признаку «находиться в Западной Сибири» среди «сибирских городов-миллионников» (В) получим «сибирские города-миллионники Западной Сибири» (С) и, соответственно, не-С («сибирские города-миллионники, не находящиеся в Западной Сибири»); далее по признаку «располагаться на реке Иртыш» получим — одноэлементный класс «город-миллионник Западной Сибири на реке Иртыш» («город Омск») (D) и класс не-D, т. е. множество «все не расположенные на Иртыше города-миллионники Западной Сибири». Схема данной классификации (рис. 10):

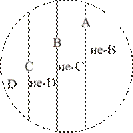
Рис. 10

Создавая классификацию, мы можем стремиться использовать только такие основание для деления, которые выражают закономерности существования предметов выделяемых множеств, и достигать этого. В таком случае может быть получена естественная классификация, научно вскрывающая закономерности своих элементов в их свойствах, позволяющая предсказывать свойства этих элементов. Если же, создавая классификацию, мы используем в качестве оснований для деления иные, чем обозначенные выше, признаки, результат имеет существенно иной характер. Возникает так называемая искусственная, или вспомогательная классификация — распределение предметов на подмножества с использованием в качестве оснований деления несущественных признаков этих предметов.

V Пример

Естественная классификация. Созданная Д.И. Менделеевым (1834-1907) периодическая система химических элементов. Искусственная классификация. Классификация учащихся группы СО-211 по начальным буквам их фамилий.

Чтобы операция деления, следовательно, и классификация оказались логически состоятельными необходимо соблюдать требования следующих четырёх правил деления понятий:

1-е правило: Деление должно быть соразмерным, т. е. сумма объёмов членов деления должна быть равна объёму делимого понятия. Если правило не соблюдается, то возникает ошибка неполное деление (указываются не все виды делимого родового понятия) либо ошибка деление с лишними членами (указываются излишние виды делимого родового понятия).

2-е правило: Деление должно производиться только по одному основанию, т. е., начиная деление, нельзя брать более чем один признак, по которому в качестве основания и будет проводиться деление. Нарушение данного правила приводит к перекрещиванию членов деления.

3-е правило: Члены деления должны исключать друг друга, т. е. они должны быть непересекающимися соподчинёнными понятиями, поэтому в их объёмах должны отсутствовать общие элементы.

4-е правило: Деление должно быть непрерывным, т. е. в ходе деления недопустимы скачки, когда, не закончив деление по выбранному основанию на исходном уровне деления, перескакивают к следующему уровню деления, применяя новое основание для деления.

4). В рамках «булевой алгебры» математической классической логики с классами можно осуществлять операции, подобные операциям арифметики: складывать, умножать, вычитать, дополнять до единицы. Операциям сложения, умножения и вычитания подлежат все классы, отвечающие понятиям в любых видах совместимости и несовместимости. Операция дополнения к классу, подразумевает исходный класс и универсальный класс, находящийся с этим исходным классом в отношении субординации. Рассмотрим сначала 3-и первые операции в их определениях и разнообразных примерах, проиллюстрированных круговыми схемами Эйлера. 1) Объединением (сложением) классов называется логическая операция по образованию из исходных классов нового класса, включающего все элементы этих исходных классов.

V Пример

Для совместимых понятий: слева — тождественных (космонавт (А) и астронавт (В) — в результате получаем класс А, или равнозначно В, т. е. А+В=А, или А+В=В и т. п.; в центре — в отношении подчинения (облако (С) и кучевое облако (D) — в результате класс D, т. е. С+D=D; справа — пересекающихся (яблоко (E) и сладкий предмет (F) — в результате новый класс G, т. е. класс «все яблоки и все сладкие предметы» (рис. 11).

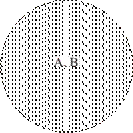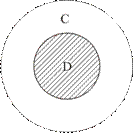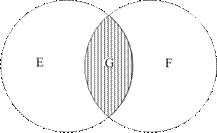Рис. 11

Для несовместимых понятий: слева — соподчинённых (кошка (А) и собака (В), как видовые понятия в отношении к родовому понятию домашнее животное (С) — в результате получаем новый класс D (его обозначение вынесено фигурной скобкой), т. е. класс «все кошки и все собаки»; в центре — противоположных (любовь (Е) и ненависть (F) — в результате получаем новый класс G (его обозначение вынесено фигурной скобкой), т. е. класс «всё, что является любовью, и всё, что является ненавистью»; справа — противоречащих (понятия ель (Н) и не ель (не-Н), исчерпывающие объём понятия дерево (I) — в результате получаем класс I (рис. 12).

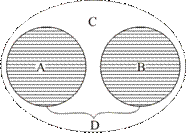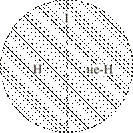Рис. 12

2) Умножением (пересечением) классов называется логическая операция по образованию из исходных классов нового класса, включающего только общие элементы этих исходных классов. По всем видам несовместимости, которая по определению подразумевает отсутствие у понятий общих элементов, применение операции логического умножения даёт нулевой класс (пустое множество).

V Пример

А — клён, В — берёза: А·В=Æ; С — любовь, D — ненависть: С·D=Æ; Е — свобода, не-Е — несвобода: Е·не-Е=Æ.

Умножение по видам совместимости:

V Пример

А — третья от Солнца планета солнечной системы, В — планета нашего местообитания: А·В=А, или А·В=В и т. п. С — горы, D — Уральские горы: С·D=D. Е — красивые местности, F — местности Южной Америки: Е· F=G (рис. 13).

Рис. 13

3) Вычитанием (разностью)классов называется логическая операция по образованию из исходного и вычитаемого классов нового класса, не включающего элементы исходного класса, которые совпадают с элементами вычитаемого класса. При применении операции вычитания к классам, которым соответствуют несовместимые понятия, т. е. понятия, по определению не имеющие общих элементов, данная операция даёт только один результат, а именно: исходный класс.

V Пример

Вычитая из класса парты (А) класс стулья (В), т. е. оперируя с соподчинёнными понятиями, получаем класс А; вычитая из класса белый предмет (С) класс чёрный предмет (D), т. е. оперируя с противоположными понятиями, получаем класс С; вычитая из класса хорошо (Е) класс нехорошо (не-Е), получаем класс Е (рис. 14).

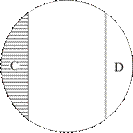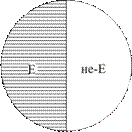Рис. 14

Теперь рассмотрим применение операции вычитания применительно к классам, которым соответствуют совместимые понятия.

Если данная операция осуществляется по отношению к классам, отвечающим тождественным понятиям, то её результатом становится нулевой класс (пустое множество), обозначаемый символом Æ. Сути такого вычитания отвечает формула:

А–В=Æ

V Пример

Если из класса город Москва вычесть класс столица Российской Федерации, то получим нулевое множество

Для классов, которым отвечают понятия в отношении подчинения, результатом применения данной операции будет новый класс, состоящий из тех элементов родового (подчиняющего) понятия, которые не совпадают с элементами видового (подчинённого) понятия.

V Пример

Подчиняющее понятие — наука (А), подчинённое — физика (В). А-В=С, где С — класс, включающий все науки кроме физики (рис. 15).

Рис. 15

Для классов, которым отвечают понятия в отношении пересечения, результатом применения данной операции будет новый класс, представленный элементами исходного понятия, не входящими в объём пересечённого с этим исходным вычитаемого понятия.

V Пример

Понятия студент (А) и спортсмен (В) пересекаются. В результате вычитания:

А-В=С, где С — класс студентов, не являющихся спортсменами (рис. 16).

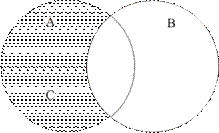
Рис. 16

Последняя рассматриваемая нами операция из арсенала «алгебры логики» — дополнение к классу. Осуществить дополнение к классу А, значит, установить по отношении к этому классу универсальный класс (U), а затем вычесть из универсального класса исходный класс (А), т. е. создать класс, состоящий из тех элементов универсального класса, которые не совпадают с элементами исходного класса. Символически результат выполнения операции дополнения к классу, обозначаемому какой-либо буквой алфавита, фиксируется этой же буквой, взятой с косым штрихом в правом верхнем регистре. Так по отношению к исходному классу А результат дополнения выражается символом — А́.

V Пример

Возьмём в качестве исходного для осуществления операции дополнения класс медведи (А), которые в биологическом понимании суть животные, следовательно, в качестве универсального класса используем класс животные (U), из которого вычтем всех медведей и получим новый класс — «все животные кроме медведей» (А́), что можно изобразить и при помощи схемы (рис. 17).

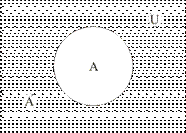
Рис. 17

Рассмотренные выше операции с классами (объёмами) понятий входят в арсенал логики классов – раздела, соответствующего и силлогистике Аристотеля, и математической логике. Логика классов в рамках математической логики отвечает операции исчисления преди­катов первого порядка,которые в логике классов и есть собственно объёмы понятий (классы). Исчисление предикатов первого порядка рассматривается во второй части данного учебного пособия.

Контрольные вопросы

I. Какие формы познания не относятся к логической проблематике и почему?

II. В чём различие субъектной, объектной, формальной, символической логик?

III. Назовите основные приёмы формирования понятий и объясните, почему они взаимозависимы?

IV. Назовите критерий отличия логики традиционной от логики нетрадиционной. К какому из этих видов следует отнести логику диалектическую?

V. Дайте определения основных понятий классической формальной логики и выявите их содержательные связи.

VI. Следует ли считать тождественными такие структуры мысли, как имя и понятие, языковое выражение и высказывание?

VII. Существует ли беззнаковое мышление и почему?

VIII. Каково значение и содержание имени «семантическая категория»?

IX.Что такое объективная истинность и формальная правильность?

X. Каковы виды и разновидности законов формальной логики? Сформулируйте основные законы мышления, охарактеризуйте их роль в позна­нии, в практике.

XI. Дайте определение понятия и укажите приёмы формирования понятий.

XII. Что такое объём и содержание понятия, каково их соотношение?

XIII. Могут ли несравнимые понятия быть совместимыми?

XIV. В чём заключается суть операций определения и деления понятий и чем данные операции в принципе отличны от операций обобщения и ограничения?

XV. Как взаимосвязаны правила явного определения понятия?

XVI. В чём суть сравнения (различении), описания, и какие ещё сходные с определением понятий приёмы Вы знаете, наряду с видами определений?

XVII. Какие правила и почему следует применять, создавая классификацию?

XVIII. Что такое класс, подкласс, элемент класса, универсальный класс и какие логические операции с ними можно осуществить?

ЧАСТЬ II