Для нормального закона

Расчет доверительных интервалов, т.е. предельных значений погрешностей, возникающих при изготовлении деталей и узлов киновидеотехники, позволяет без построения кривых распределения оценить ширину поля рассеяния погрешностей.

Расчет доверительных интервалов позволяет оценить поле распределения результатов измерения и их погрешностей на основании ограниченного числа имеющихся экспериментальных данных. Приведем методику расчета доверительного интервала, когда результаты измерения подчиняются нормальному закону распределения.

В начале расчета задают необходимый уровень надежности g. Эта надежность равна вероятности того, что разность между каждым случайным результатом и средним арифметическим всех результатов не превысит допустимого отклонения. Это отклонение и определяет ширину доверительного интервала ±d

1. Надежность расчетов задают

g = P{|X-x­| ≤d} = P(X-d £ x £ X+d) = P(-∞< x £X+d) –P(-∞<x £ X-d) = F(X+d) – F(X-d). (1.8)

2.

В то же время нормированная интегральная функция нормального распределения

, (1.9)

где первое слагаемое – половина интеграла Эйлера-Пуассона

, второе слагаемое – интеграл вероятности (табличное значение); - нормированный параметр распределения.

3.Формула для расчета доверительного интервала

Подставим формулу (1,9), являющуюся табличным выражением нормированной интегральной функции нормального распределения, в формулу (1.8), тогда

где – квантиль нормированного нормального распределения (табличное значение).

Таким образом, .

В итоге, алгоритм расчета доверительного интервала следующий:

- задается уровень надежности γ, ;

- в таблице значений интеграла вероятности (Приложение 1) по находят ,

-

- рассчитывают ; значение погрешности будет лежать в интервале

.(1.10)

Приведенная методика расчета доверительных интервалов применяется при нормальном распределении параметров (значений геометрических параметров, значений физико- технических и выходных качественных характеристик, а также их погрешностей). При законах распределения, отличных от нормального, расчет доверительных интервалов усложняется [13].

Расчет доверительного интервала при неизвестном законе распределения вероятности результата измерения или погрешности

Вероятность того, что результат измерения х окажется за пределами доверительного интервала при любом законе распределения вероятности

.

Можно использовать функцию

.

График этой функции приведен на рис.

Тогда

, т.е. вероятность станет меньше, если функцию заменить квадратичной функцией , которая при всех х больше , т.е.

.

Вероятность попадания результата измерения в доверительный интервал

Данное неравенство называется неравенством Чебышева П.П., оно устанавливает нижнюю границу вероятности того, что ни при каком законе распределения вероятности результат измерения не окажется за пределами доверительного интервала:

t=3: P=1-1/3≈0,89;

t=2: P=1-1/4≈0,75…

2.2.11. Приближенные методы оценки точности. Описание погрешностей моментами

Моменты – числовые характеристики случайных величин. Их рассчитывают для приближенного описания законов распределения случайных результатов измерения или их погрешностей.

Практическое значение имеют следующие моменты:

1.Начальные моменты:

,

-порядок момента,

Первый начальный момент – математическое ожидание (среднее арифметическое значение), определяет центр распределения, соответствует координате центра тяжести фигуры, ограниченной кривой распределения:

2.Центральные моменты:

- порядок момента.

Первый центральный момент равен 0.

Второй центральный момент

В дискретном виде:

- дисперсия, определяет ширину поля рассеяния результатов измерения.

Среднеквадратическое отклонение .

Третий центральный момент характеризует асимметрию кривой распределения, для количественной оценки используется характеристика асимметрии (скошенность, skewness )

.

Четвертый центральный момент характеризует островершинность или плосковершинность кривой распределения, количественно оценивается эксцессом

.

Расчет четырех моментов позволяет восстановить кривую распределения:

Рис. Построение кривой распределения по моментам распределения

2.2.12. Обработка результатов измерений, не подчиняющихся нормальному закону распределения.

(Робастость.!!!!)

Можно использовать следующие способы обработки результатов:

1.Когда нет возможности строго определить закон распределения вероятности результатов измерения, можно использовать статистическую проверку гипотезы о виде распределения.

Проверка гипотезы о нормальности распределения.

При проверке гипотезы о нормальности распределения проверяют равенство среднего арифметического и дисперсии эмпирического распределения математическому ожиданию и дисперсии нормального распределения.

Мера расхождения по Пирсону обозначается (критерий согласия, критерий Пирсона, «хи»- квадрат, )

, (1.11)

где , - частоты, равные числу результатов в каждом интервале, меньших или равных его правой или больших левой границы; 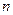- общее число результатов; - теоретическая вероятность; - ширина интервала; - плотности в серединах интервалов; - плотности нормированного распределения, определяются по табл. Приложения 2 по ; - нормированное отклонение от среднего арифметического; - среднее арифметическое; - среднеквадратическое отклонение; - число интервалов.

Для каждого интервала вычисляют величины , суммируют, находят меру расхождения . Если в интервал входят 5 и меньше значений, этот интервал объединяют с соседним.

Определяют число степеней свободы , где - число разрядов гистограммы; - число независимых связей, к ним относятся: равенство среднего арифметического эмпирического и теоретического распределений; равенство математических ожиданий; равенство суммы частностей единице.

Все три условия в данном случае имеют место,

поэтому .

Задают уровень значимости , где - принятая доверительная вероятность (надежность).

По табл. Приложения 3 находят значения

и .

Если ≤ ≤ ,

то распределение считается нормальным.

Номер интервала, i

Середина интервала, хi , мм

Частота, mi

xi-X , мм

Нормированное отклонение t = (xi-X) / 6

Плотность нормированного распределения p(ti) Приложение.2

Плотность в середине интервала p(xi)=p(ti) / 6

Теоретическая вероятность nPi= ∆ xi p(xi)n

Отклонение χi 2

При малом числе результатов 11<n<50 нормальность распределения проверяется обязательным соответствием данного распределения двум критериям.

Первый критерий – статистика d

. (1.12)

При выбранном уровне значимости q₁ должно выполняться условие

Граничные значения статистик определяют по Приложению 4.

Второй критерий – условие ,

где m₁ – число разностей, которые соответствуют условию ; - среднеквадратическое отклонение; - квантиль интегральной функции Ф нормированного нормального распределения, его величина приведена в Приложении 5 , причем, ; Р₂ - доверительная вероятность для второго критерия, , m – граничное число разностей, зависящее от уровня значимости и количества результатов (Приложение 6).

Если вероятность распределения результатов измерения не подчиняется нормальному закону, их точность может быть определена:

2. При особо точных измерениях – устанавливают закон распределения

3. при приближенных оценках рассчитывают доверительный интервал или моменты распределения

4. если закон распределения незначительно отличается от нормального, можно использовать робастые (устойчивые) к большим отклонениям методы обработки данных или просто отбросить большие отклонения, использовать усеченный нормальный закон.

При этом используют робастые оценки, например, медиану

Можно большие отклонения не отбрасывать, а заменить их на ближайшие из оставшихся или включить с малыми весовыми коэффициентами. Среднее арифметическо не является робастой оценкой, т.к. делает большие отклонения доминирующими. Ослабление влияния больших отклонений на оценку среднего значения достигается, например, при использовании суммы отклонений от среднего значения или ее функции. Авторы таких оценок – Хубер, Хампел, Анрюс, Тьюки и др.

Пример:

Получены результаты

X= 9,6,13,5,8,1

Среднее арифметическое этого ряда

Пусть появился результат x=63. Тогда

Если использовать медиану, ранжированный ряд:

1,5,6,8,9,13, медиана: .

Во втором случае:

1,5,6,8,9,13,63, медиана:

, т.е. медиана оказалась устойчивой к большому отклонению.

2.2.12. Точность при многократных измерениях

Различают многократные равноточные и неравноточные измерения.

При равноточных многократных измерениях используют средства измерения одинаковой точности (с равными Ϭ).

Дисперсия такого измерения

, т.е. точность повышается в раз

Для неравноточных многократных измерений, когда результаты получены с помощью различных средств измерения, а для каждого средства измерения вероятность распределения подчиняется нормальному закону, целесообразно использовать функцию правдоподобия:

…

- среднее взвешенное, в котором в числителе отдельные значения результатов измерения суммируются с «весами», обратно пропорциональными их дисперсиям. Более точным значениям придается больший вес. Нормированный вес каждого отдельного результата измерения

.

Дисперсия средневзвешенного

.

Можно пример.

2.1.13.Критерий ничтожных погрешностей

Суммарная погрешность

.

Погрешность считают ничтожной, если

, т.е. .

Использование этого критерия позволяет выделить те величины, которые существенно влияют на суммарную погрешность результата, снизить точность измерения тех величин, погрешности которых ничтожны. При большом числе погрешностей может быть .

2.1.14. Исключение грубых погрешностей и промахов

Для корректного анализа результатов измерения необходимо исключить грубые погрешности и промахи

Погрешность является грубой, если , в этом случае максимальное значение надо отбросить и проверить следующее максимальное значение, - доверительная вероятность.

Погрешность является промахом, если , этот результат также надо отбросить.

После исключения грубых погрешностей и промахов пересчитывают статистические параметры.

2.1.15. Алгоритм анализа результатов измерения.

Цель анализа результатов – оценка точности измерений.

Последовательность:

1. Исключают систематические погрешности

2.Проверяют гипотезу о нормальности распределения

3. Исключают НИЧТО грубые погрешности и промахи.

4. Определяют ничтожные погрешности, исключают их.

5. Вычисляют статистические параметры

6. Рассчитывают случайные погрешности при заданном уровне вероятности.