Системы счисления и коды используемые в цифровой технике

Лекция №10

Фильтры на основе пьезокерамики

Кварцевые фильтры

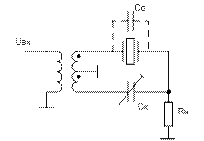
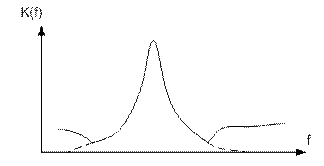
Рис. 10.1 однозвенный КФ

Чтобы скомпенсировать внеполосное прохождение сигнала, ставят C_к

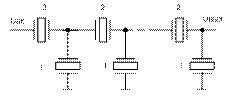
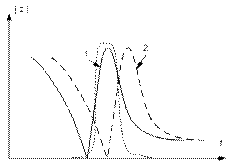
Рис.10.2 многозвенный лестничный фильтр

Полоса пропускания. у таких фильтров, как правило, менее 1 кГц. Коэффициент ослабления – до 70 дБ. Коэффициент прямоугольности приближается к 2 и меньше.

2. Интегральные кварцевые фильтры на объёмных акустических волнах

Рис. 10.3 Фильтр на ОАК

Рабочие частоты 1-100МГц

s_с ³ 80 дБ

Пьезокерамические фильтры

Вместо кварца - титанат бария, титонат-цирконат свинца и др.

Строится по схеме лестничного типа. Добротность 300 ¸ 500.

Рабочие частоты 100-1000 кГц (465 кГц)

Полоса пропускания у таких фильтров, 1-10 кГц

Коэффициент прямоугольности приближается к 3-5.

Пьезомеханические фильтры.

Металлическая пластина с нанесенными пъезоэлементами

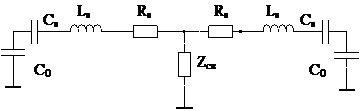
Рис. 10.4 эквивалентная электрическая схема

Фильтры на ПАВ

Полосовой фильтр на ПАВ – два встречно – штыревых преобразователя напылённые на поверхность пьезоэлектрической подложки.

Рис. 10.5 фильтр на ПАВ, структура

w – величина перекрытия (аподизация)

если l=d, то акустические колебания синхронно складываются, наступает резонанс.

Частота резонанса fр = V/d

V= 3 10¹⁵м/сек

АЧХ определяется в основном конфигурацией ВШП1.

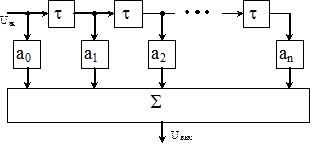
Рис.10.6 Эквивалентная схема

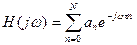10.1

1. a₁ = a₂ = … = a_n 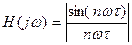~ sin(х)/х 10.2

2. Если a_n ~ sin(х)/х 10.3

т.е. a_n ~ w -переменная

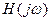® “ ” 10.4

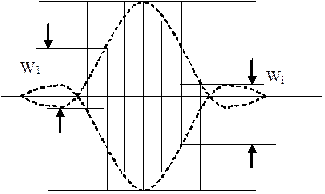Рис. 10.7 ВШП1, w -переменная

f_раб от 10 МГц до единиц ГГц

Цифровая техника

Аналоговые сигналы представляются в дискретном виде:
- квантование по уровню;
- квантование по времени

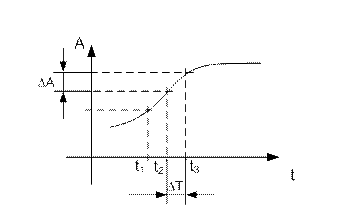
Рис. 10.8

∆А –интервал дискретизации по уровню;

А₁,А₂,А₃…. А_i …– значения амплитуд отсчетов;

DT–интервал дискретизации по времени;

t₁,t₂,t₃…. t_i …– моменты отсчета

А_i(t_i) à n_i(t_i) коды амплитуд (оцифровка сигнала)

Достоинства ЦТ:
- высокий уровень развития элементарной базы;
- высокая помехозащищенность;
- простата хранения информации;
- большие времена хранения информации;
- контролируемая точность математических операций (контролируемая)

Недостатки:
- погрешность (дискретизация);
- «громоздкость»;
- трудность работы в реальном масштабе времени;

Системы счисления и коды используемые в цифровой технике

Информация задается в виде чисел. Число – набор цифр.

Закон, по которому из набора чисел составляется число, определяет систему счисления.

В цифровой технике используется позиционная система счисления.

Значение каждой цифры в позиционной системе счисления зависит не только от ее величины, но и от ее положения (позиции) среди других цифр в данном числе.

Позиционные системы счисления отличаются основанием.

Основание позиционной системы – число, равное количество цифр необходимых для отображения всех чисел в пределах одного разряда.

Основания в цифровой технике: 2, 8, 16.

Число в позиционной системе м.б представлено

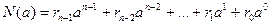(10.9)

a – основание системы;

r – вес разряда.

n – разрядность числа

В цифровой технике используются в основном двоичная система 0, 1. Почему?

Пример: 321₁₀

321₁₀ = 3 10²+2 10¹ +1 10⁰

321₂ = 101000001

Повторить! прямое и обратное преобразование десятичных и двоичных чисел

В цифровой технике используются также двоично- десятичные числа(для предоставления десятичных чисел в двоичной форме) каждый разряд дес. числа представляется дв. числом.

Пример: 321₁₀à 0011| 0010| 0001

В восьмеричной системе: 0,1…7

В шестнадцатеричной системе: 0, 1…9, A, B, С, D, E, F

Двоичная арифметика

Сложение, вычитание, умножение и деление в двоичной системе, как и в десятеричной

Повторить! Сложение, вычитание, умножение и деление в двоичной системе

В цифровой технике используется прямой код 5à0101; 9à1001

В цифровой технике используется обратный (инверсный) код.

01011100 à 10100011 т. е. замена 1à 0, а 0à1

В цифровой технике также используетсядополнительныйкод:

дополнительный код = инверсный код + 1